Участник:Ilya4870/Алгоритм разбиения графа методом рекурсивной координатной бисекции

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

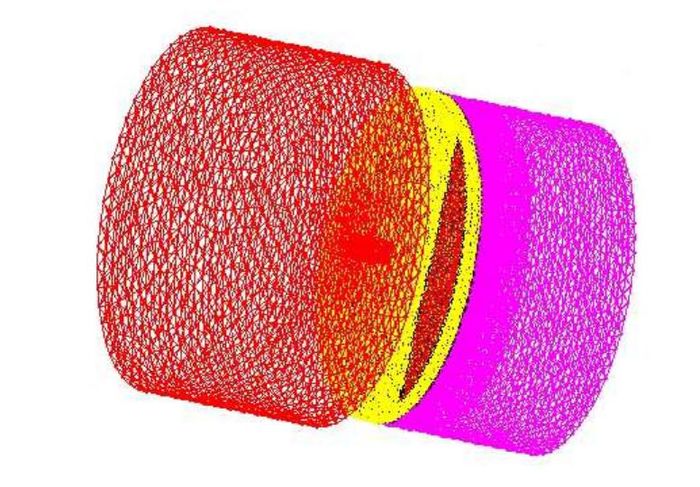
Задача рациональной декомпозиции расчетных сеток возникает при численном моделировании на высокопроизводительных вычислительных системах проблем механики сплошных сред, импульсной энергетики, электродинамики и многих других. Такие задачи сводятся к более общей задачи - разбиение вершин графа. Оптимальным считается разбиение на домены, при котором выровнен суммарный вес вершин в доменах и минимизирован суммарный вес разрезанных ребер (разрезанное ребро – ребро, соединяющее вершины из разных доменов). Одним из методов разбиения вершин графа на равные по мощности блоки является метод рекурсивной координатной бисекции.

На каждом этапе рекурсивной бисекции область разбивается на две части. Соотношение размеров частей зависит от количества доменов, которые должны быть образованы в каждой из частей. Полученные подобласти разбиваются дальше аналогичным образом до тех пор, пока в подобластях не останется по одному домену. При рекурсивной координатной бисекции на этапе разбиения выбирается координатная ось, вдоль которой область имеет наибольшую протяженность. Область разбивается перпендикулярно полученной оси. Достоинством данного метода является то, что при разбиении на равные домены числа вершин в получаемых доменах отличаются не больше, чем на единицу. Другими достоинствами являются экономичное использование памяти и относительная быстрота работы.

В данном разделе представляется самый первый вариант описания тех задач (или классов задач), для решения которых предназначен алгоритм. В описании поясняются особенности как алгоритма, так и объектов, с которыми он работает. Если описание соответствует целому классу схожих по структуре алгоритмов, либо же посвящено описанию отдельного представителя некоторого класса, то это здесь указывается явно. Описываются базовые математические свойства и структура входных данных. При необходимости, в описании могут присутствовать формулы, а также даваться ссылки на описания других используемых алгоритмов. Данное описание должно быть достаточным для однозначного понимания сути решаемой задачи.

1.2 Математическое описание алгоритма

Пусть [math]G = (V,E)[/math] – неориентированный граф, где [math]V = \{v_i\}[/math] – множество вершин, [math]E = \{e_{ij}\}[/math] – множество рёбер. И вершины, и рёбра, имеют целочисленные веса [math]|v_i|[/math] и [math]|e_{ij}|[/math], соответственно.

Декомпозиция является отображением множества вершин [math]V[/math] на заданное число [math]p[/math] доменов [math]S_j[/math] такое, что каждая вершина [math]v_i[/math] принадлежит некоторому домену [math]S_j[/math], и [math]S_k \cap S_m = \emptyset[/math].

Суммарный вес вершин в домене [math]S_j[/math] равен сумме весов вершин, принадлежащих этому домену: [math]|S_j| = \sum_{i}{|v_i|}, v_i \in S_j[/math].

Суммарный вес разрезанных рёбер равен сумме весов рёбер, соединяющих вершины из разных доменов: [math]|E_c|=\sum_{ij}{|e_ij|}, v_i \in S_k, v_j \in S_m, k \lt m[/math].

Каждый домен [math]S_j[/math] является некоторым подграфом [math]G^j = (V^j, E^j)[/math] графа [math]G = (V, E)[/math], где [math]V^j \subseteq V, E^j \subseteq E[/math]. Домен является связным, если его граф состоит из одной компоненты связности, то есть между любой парой вершин этого графа существует как минимум один путь.

Требуется найти такое разбиение множества вершин [math]V[/math] на заданное число [math]p[/math] связных доменов [math]S_j[/math], при котором:

• выровнен суммарный вес вершин в доменах: [math]|S_j| \approx |V|/p[/math],[math](1)[/math]

• минимизирован суммарный вес разрезанных рёбер: [math]min(|E_c|)[/math].[math](2)[/math]

Используя обозначения выше, определим:

• Входные данные алгоритма: множество координат вершин [math]C = \{c_i\}[/math] графа [math]G = (V, E)[/math], где [math]c_i = (v_i^x, v_i^y, v_i^z)[/math] - координаты вершины [math]v_i \in V[/math], число доменов [math]p[/math].

• Выходные данные алгоритма: разбиение множества вершин [math]V[/math] на заданное число [math]p[/math] доменов [math]S_j[/math].

Основные этапы алгоритма:

• вычисляются протяжённости осей: [math]l_k = |max(v_i^k) - min(v_i^k)|[/math] для [math]k = x, y, z[/math],

• производится сортировка множества [math]C[/math] по координате, соответствующей наибольшей [math]l_k[/math],

• множество [math]C[/math] разбивается на две части в соответствии с новым порядком элементов, то есть перпендикулярно координатной оси, вдоль которой она имеет наибольшую протяжённость; соотношение размеров частей зависит от количества доменов, которые должны быть образованы в каждой из частей,

• полученные подмножества разбиваются дальше аналогичным образом до тех пор, пока на очередном шаге рекурсии в них не останется по одному домену.

1.3 Вычислительное ядро алгоритма

Большую часть времени занимает сортировка массива координат вершин [math]C[/math], выполняемая на каждом шаге рекурсии. Сортировка может быть выполнена любым способом, в зависимости от реализации.

1.4 Макроструктура алгоритма

Если алгоритм использует в качестве составных частей другие алгоритмы, то это указывается в данном разделе. Если в дальнейшем имеет смысл описывать алгоритм не в максимально детализированном виде (т.е. на уровне арифметических операций), а давать только его макроструктуру, то здесь описывается структура и состав макроопераций. Если в других разделах описания данного алгоритма в рамках AlgoWiki используются введенные здесь макрооперации, то здесь даются пояснения, необходимые для однозначной интерпретации материала. Типичные варианты макроопераций, часто встречающиеся на практике: нахождение суммы элементов вектора, скалярное произведение векторов, умножение матрицы на вектор, решение системы линейных уравнений малого порядка, сортировка, вычисление значения функции в некоторой точке, поиск минимального значения в массиве, транспонирование матрицы, вычисление обратной матрицы и многие другие.

Описание макроструктуры очень полезно на практике. Параллельная структура алгоритмов может быть хорошо видна именно на макроуровне, в то время как максимально детальное отображение всех операций может сильно усложнить картину. Аналогичные аргументы касаются и многих вопросов реализации, и если для алгоритма эффективнее и/или технологичнее оставаться на макроуровне, оформив макровершину, например, в виде отдельной процедуры, то это и нужно отразить в данном разделе. Выбор макроопераций не однозначен, причем, выделяя различные макрооперации, можно делать акценты на различных свойствах алгоритмов. С этой точки зрения, в описании одного алгоритма может быть представлено несколько вариантов его макроструктуры, дающих дополнительную информацию о его структуре. На практике, подобные альтернативные формы представления макроструктуры алгоритма могут оказаться исключительно полезными для его эффективной реализации на различных вычислительных платформах.

1.5 Схема реализации последовательного алгоритма

0. Вычисляются минимумы и максимумы по каждой из координат, определяющие параллелепипед, охватывающий вершины данной област. Далее запускается процесс рекурсии, на каждом шаге которого выполняется следующее:

1. Определяется координата j, вдоль которой параллелепипед, разрезающийся на данном этапе, имеет наибольшую протяженность.

2. Определяется количество доменов, которое делится на данном этапе. В левую часть (вершины с меньшей координатой j) попадет половина доменов. Сначала набираются домены нулевого типа, потом, если они закончились, первого, и т.д. до получения нужного числа доменов в левой части. Подсчитывается общее число вершин n1, которое окажется в этих доменах. В правой части будут сформированы оставшиеся домены.

3. Пусть все вершины в параллелепипеде имеют координаты j, принадлежащие интервалу [minj, maxj]. Интервал делится на K равных малых интервалов. K – некоторая константа. Подсчитываются количества вершин, принадлежащие каждому малому интервалу. Исходя из того, что в левую часть должна попасть n1 вершина с меньшей координатой j, определяется, в какой малый интервал [fromj, toj] попадает медиана. Затем вершины из интервала [fomj, toj] записываются в отдельный массив, отсортированный по всем координатам. Определяется медиана – последняя вершина, которая попадет в левую часть.

4. Если предполагается построение локальных деревьев, для вершины i двоичного дерева запоминаются данные о медиане: ее координаты, номер вершины медианы и номер координаты j, по которой проводилось деление.

5. Проводится разделение данных по аналогии с обменной сортировкой с разделением Хоару (быстрая сортировка), чтобы на следующих этапах просматривались только вершины из разбиваемой области. Два указателя, beg и end, выставляются на начало и на конец массива данных, соответственно. Вершина, на которую указывает указатель beg, равнивается с медианой по всем координатам, и, если она попадает в левую часть параллелепипеда, указатель beg сдвигается к следующей вершине. Так до тех пор, пока указатель beg не остановится на вершине, которая должна попасть в правую часть. Указатель end конца массива сдвигается влево до тех пор, пока не остановится на вершине, которая должна попасть в левую часть. Если указатель beg находится левее указателя end, вершины, на которые указывают указатели, меняются местами, после чего указатель beg сдвигается вправо, а end – влево. Если указатель beg все еще левее указателя end, весь процесс повторяется снова. Если после выхода из цикла указатели указывают на одну и ту же вершину, она сравнивается с медианой по всем координатам, и если вершина попадает в левую часть, указатель beg сдвигается к следующей вершине. Указатель beg определяет начало массива данных правой части.

6. По рекурсии левая и правая части отправляются на деление. Левой части передается указатель на начало исходного массива данных и число вершин n1. Максимальные координаты параллелепипеда остаются теми же, только максимальная координата j приравнивается к координате j медианы. Передается число доменов каждого вида, которое будет в левой части. Номер вершины двоичного дерева, отвечающей за деление левой части, будет равным (2 · i). Правой части передается указатель beg в качестве нового указателя на массив данных и оставшееся число вершин. Минимальная координата j приравнивается к координате медианы. Передаются числа доменов каждого вида. Номер вершины двоичного дерева, отвечающей за деление правой части, будет равным (2 · i + 1). 7. Перед делением каждой из частей проверяется, сколько доменов осталось в данной части. Если остался только один домен, то все вершины помещаются в данный домен. Домены считаются по порядку от номера gr0 первого домена. Если предполагается построение локальных деревьев, в лист дерева записывается номер домена. Запоминается максимальный номер вершины. Если в части осталось больше одного домена, она отправляется на деление.

Рисунок 1. Пример координатной бисекции на три домена.

Алгоритм работает только с координатами вершин и не учитывает связи между ними, что делает его экономичным по памяти.

Описание схемы реализации вполне может содержать и словесные пояснения, отражающие какие-либо тонкие нюансы самого алгоритма или его реализации. Уже в данном разделе можно сказать про возможный компромисс между объемом требуемой оперативной памяти и временем работы алгоритма, между используемыми структурами данных и степенью доступного параллелизма. В частности, часто возникает ситуация, когда можно ввести дополнительные временные массивы или же отказаться от использования специальных компактных схем хранения данных, увеличивая степень доступного параллелизма.

1.6 Последовательная сложность алгоритма

[math]O(n) \approx n \log_2{n} \log_2{p}, n = |V|.[/math]

В данном разделе описания свойств алгоритма приводится оценка его последовательной сложности, т.е. числа операций, которые нужно выполнить при последовательном исполнении алгоритма (в соответствии с п.1.5). Для разных алгоритмов понятие операции, в терминах которой оценивается его сложность, может существенно различаться. Это могут быть операции для работы с вещественными числами, целыми числами, поразрядные операции, обращения в память, обновления элементов массива, элементарные функции, макрооперации и другие. В LU-разложении преобладают арифметические операции над вещественными числами, а для транспонирования матриц важны лишь обращения к памяти: это и должно найти отражение в описании.

Если выбор конкретного типа операций для оценки сложности алгоритма не очевиден, то нужно привести обоснование возможных вариантов. В некоторых случаях можно приводить оценку не всего алгоритма, а лишь его вычислительного ядра: в таком случае это нужно отметить, сославшись на п.1.1.

Например, сложность алгоритма суммирования элементов вектора сдваиванием равна [math]n-1[/math]. Сложность быстрого преобразования Фурье (базовый алгоритм Кули-Тьюки) для векторов с длиной, равной степени двойки – [math]n\log_2n[/math] операций комплексного сложения и [math](n\log_2n)/2[/math] операций комплексного умножения. Сложность базового алгоритма разложения Холецкого (точечный вариант для плотной симметричной и положительно-определенной матрицы) это [math]n[/math] вычислений квадратного корня, [math]n(n-1)/2[/math] операций деления, по [math](n^3-n)/6[/math] операций умножения и сложения (вычитания).

1.7 Информационный граф

Это очень важный раздел описания. Именно здесь можно показать (увидеть) как устроена параллельная структура алгоритма, для чего приводится описание и изображение его информационного графа (графа алгоритма [1]). Для рисунков с изображением графа будут составлены рекомендации по их формированию, чтобы все информационные графы, внесенные в энциклопедию, можно было бы воспринимать и интерпретировать одинаково. Дополнительно можно привести полное параметрическое описание графа в терминах покрывающих функций [1].

Интересных вариантов для отражения информационной структуры алгоритмов много. Для каких-то алгоритмов нужно показать максимально подробную структуру, а иногда важнее макроструктура. Много информации несут разного рода проекции информационного графа, выделяя его регулярные составляющие и одновременно скрывая несущественные детали. Иногда оказывается полезным показать последовательность в изменении графа при изменении значений внешних переменных (например, размеров матриц): мы часто ожидаем "подобное" изменение информационного графа, но это изменение не всегда очевидно на практике.

В целом, задача изображения графа алгоритма весьма нетривиальна. Начнем с того, что это потенциально бесконечный граф, число вершин и дуг которого определяется значениями внешних переменных, а они могут быть весьма и весьма велики. В такой ситуации, как правило, спасают упомянутые выше соображения подобия, делающие графы для разных значений внешних переменных "похожими": почти всегда достаточно привести лишь один граф небольшого размера, добавив, что графы для остальных значений будут устроены "точно также". На практике, увы, не всегда все так просто, и здесь нужно быть аккуратным.

Далее, граф алгоритма - это потенциально многомерный объект. Наиболее естественная система координат для размещения вершин и дуг информационного графа опирается на структуру вложенности циклов в реализации алгоритма. Если глубина вложенности циклов не превышает трех, то и граф размещается в привычном трехмерном пространстве, однако для более сложных циклических конструкций с глубиной вложенности 4 и больше необходимы специальные методы представления и изображения графов.

В данном разделе AlgoWiki могут использоваться многие интересные возможности, которые еще подлежат обсуждению: возможность повернуть граф при его отображении на экране компьютера для выбора наиболее удобного угла обзора, разметка вершин по типу соответствующим им операций, отражение ярусно-параллельной формы графа и другие. Но в любом случае нужно не забывать главную задачу данного раздела - показать информационную структуру алгоритма так, чтобы стали понятны все его ключевые особенности, особенности параллельной структуры, особенности множеств дуг, участки регулярности и, напротив, участки с недерминированной структурой, зависящей от входных данных.

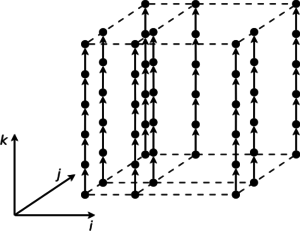
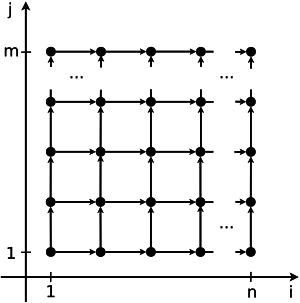
На рис.1 показана информационная структура алгоритма умножения матриц, на рис.2 - информационная структура одного из вариантов алгоритма решения систем линейных алгебраических уравнений с блочно-двухдиагональной матрицей.

Рис.1. Информационная структура алгоритма умножения матриц

Рис.2. Информационная структура одного из вариантов алгоритма решения систем линейных алгебраических уравнений с блочно-двухдиагональной матрицей

1.8 Ресурс параллелизма алгоритма

Исходя из того, что метод является геометричическим, алгоритм обладает координатным параллелизмом. Таким образом структара параллеьного алгоритма включает в себя следующие этапы:

1. Начальное распределение вершин по процессорам. Начальное распределение может быть любым, например, в соответствии с порядковыми номерами вершин.

2. Определение числа доменов, которые должны быть сформированы на каждом из процессоров, и количества вершин в них.

3. Рекурсивная координатная бисекция вершин по процессорам. На каждом этапе сначала вычисляется координатная ось, вдоль которой область имеет наибольшую протяженность. Затем блок вершин бьется на две части перпендикулярно данной оси . Группа процессоров делится на две, далее каждая из групп делит свой блок вершин аналогичным образом. Для разделения блока вершин используется параллельная сортировка. После рекурсивной координатной бисекции вершин по процессорам на процессорах оказывается столько вершин, сколько должно быть в образуемых на них доменах.

4. Локальная рекурсивная координатная бисекция вершин по доменам. Дальнейшее разбиение на домены проводится локально на каждом процессоре.

Здесь приводится оценка параллельной сложности алгоритма: числа шагов, за которое можно выполнить данный алгоритм в предположении доступности неограниченного числа необходимых процессоров (функциональных устройств, вычислительных узлов, ядер и т.п.). Параллельная сложность алгоритма понимается как высота канонической ярусно-параллельной формы [1]. Необходимо указать, в терминах каких операций дается оценка. Необходимо описать сбалансированность параллельных шагов по числу и типу операций, что определяется шириной ярусов канонической ярусно-параллельной формы и составом операций на ярусах.

Параллелизм в алгоритме часто имеет естественную иерархическую структуру. Этот факт очень полезен на практике, и его необходимо отразить в описании. Как правило, подобная иерархическая структура параллелизма хорошо отражается в последовательной реализации алгоритма через циклический профиль результирующей программы (конечно же, с учетом графа вызовов), поэтому циклический профиль (п.1.5) вполне может быть использован и для отражения ресурса параллелизма.

Для описания ресурса параллелизма алгоритма (ресурса параллелизма информационного графа) необходимо указать ключевые параллельные ветви в терминах конечного и массового параллелизма. Далеко не всегда ресурс параллелизма выражается просто, например, через координатный параллелизм или, что то же самое, через независимость итераций некоторых циклов (да-да-да, циклы - это понятие, возникающее лишь на этапе реализации, но здесь все так связано… В данном случае, координатный параллелизм означает, что информационно независимые вершины лежат на гиперплоскостях, перпендикулярных одной из координатных осей). С этой точки зрения, не менее важен и ресурс скошенного параллелизма. В отличие от координатного параллелизма, скошенный параллелизм намного сложнее использовать на практике, но знать о нем необходимо, поскольку иногда других вариантов и не остается: нужно оценить потенциал алгоритма, и лишь после этого, взвесив все альтернативы, принимать решение о конкретной параллельной реализации. Хорошей иллюстрацией может служить алгоритм, структура которого показана на рис.2: координатного параллелизма нет, но есть параллелизм скошенный, использование которого снижает сложность алгоритма с [math]n\times m[/math] в последовательном случае до [math](n+m-1)[/math] в параллельном варианте.

Рассмотрим алгоритмы, последовательная сложность которых уже оценивалась в п.1.6. Параллельная сложность алгоритма суммирования элементов вектора сдваиванием равна [math]\log_2n[/math], причем число операций на каждом ярусе убывает с [math]n/2[/math] до [math]1[/math]. Параллельная сложность быстрого преобразования Фурье (базовый алгоритм Кули-Тьюки) для векторов с длиной, равной степени двойки - [math]\log_2n[/math]. Параллельная сложность базового алгоритма разложения Холецкого (точечный вариант для плотной симметричной и положительно-определенной матрицы) это [math]n[/math] шагов для вычислений квадратного корня, [math](n-1)[/math] шагов для операций деления и [math](n-1)[/math] шагов для операций умножения и сложения.

1.9 Входные и выходные данные алгоритма

• Входные данные алгоритма: множество координат вершин [math]C = \{c_i\}[/math] графа [math]G = (V, E)[/math], где [math]c_i = (v_i^x, v_i^y, v_i^z)[/math] - координаты вершины [math]v_i \in V[/math]. Таким образом, множество воординат вершин может быть передано как массив трёхмерных векторов. Число доменов [math]p[/math] передается в виде натурального числа, не может превышать число вершин.

• Выходные данные алгоритма: разбиение множества вершин [math]V[/math] на заданное число [math]p[/math] доменов [math]S_j[/math]. Эти данные могут быть записаны как массив четырехмерных векторов координат вершин, четвертой координатой будет номер домена, которому принадлежит вершина.

Количество элементов массива входных данных может быть очень большим, например, алгоритм используется для нерегулярных сеток, содержащих [math]10^9[/math] и более вершин. В настоящее время такие сетки невозможно разместить в памяти одного процессора (на гексаэдральную сетку, состоящую из [math]1.2 \dot 10^8[/math] ячеек, требуется порядка 200 ГБ), поэтому для декомпозиции нужен параллельный алгоритм.

1.10 Свойства алгоритма

Описываются прочие свойства алгоритма, на которые имеет смысл обратить внимание на этапе реализации. Как и ранее, никакой привязки к конкретной программно-аппаратной платформе не предполагается, однако вопросы реализации в проекте AlgoWiki всегда превалируют, и необходимость обсуждения каких-либо свойств алгоритмов определяется именно этим.

Весьма полезным является соотношение последовательной и параллельной сложности алгоритма. Оба понятия мы рассматривали ранее, но здесь делается акцент на том выигрыше, который теоретически может дать параллельная реализация алгоритма. Не менее важно описать и те сложности, которые могут возникнуть в процессе получения параллельной версии алгоритма.

Вычислительная мощность алгоритма равна отношению числа операций к суммарному объему входных и выходных данных. Она показывает, сколько операций приходится на единицу переданных данных. Несмотря на простоту данного понятия, это значение исключительно полезно на практике: чем выше вычислительная мощность, тем меньше накладных расходов вызывает перемещение данных для их обработки, например, на сопроцессоре, ускорителе или другом узле кластера. Например, вычислительная мощность скалярного произведения двух векторов равна всего лишь [math]1[/math], а вычислительная мощность алгоритма умножения двух квадратных матриц равна [math]2n/3[/math].

Вопрос первостепенной важности на последующем этапе реализации - это устойчивость алгоритма. Все, что касается различных сторон этого понятия, в частности, оценки устойчивости, должно быть описано в данном разделе.

Сбалансированность вычислительного процесса можно рассматривать с разных сторон. Здесь и сбалансированность типов операций, в частности, арифметических операций между собой (сложение, умножение, деление) или же арифметических операций по отношению к операциям обращения к памяти (чтение/запись). Здесь и сбалансированность операций между параллельными ветвями алгоритма. С одной стороны, балансировка нагрузки является необходимым условием эффективной реализации алгоритма. Вместе с этим, это очень непростая задача, и в описании должно быть отмечено явно, насколько алгоритм обладает этой особенностью. Если обеспечение сбалансированности не очевидно, желательно описать возможные пути решения этой задачи.

На практике важна детерминированность алгоритмов, под которой будем понимать постоянство структуры вычислительного процесса. С этой точки зрения, классическое умножение плотных матриц является детерминированным алгоритмом, поскольку его структура при фиксированном размере матриц никак не зависит от элементов входных матриц. Умножение разреженных матриц, когда матрица хранятся в одном из специальных форматов, свойством детерминированности уже не обладает: его свойства, например, степень локальности данных зависит от структуры разреженности входных матриц. Итерационный алгоритм с выходом по точности также не является детерминированным: число итераций, а значит и число операций, меняется в зависимости от входных данных. В этом же ряду стоит использование датчиков случайных чисел, меняющих вычислительный процесс для различных запусков программы. Причина выделения свойства детерминированности понятна: работать с детерминированным алгоритмом проще, поскольку один раз найденная структура и будет определять качество его реализации. Если детерминированность нарушается, то это должно быть здесь описано вместе с описанием того, как недетерминированность влияет на структуру вычислительного процесса.

Серьезной причиной недетерминированности работы параллельных программ является изменение порядка выполнения ассоциативных операций. Типичный пример - это использование глобальных MPI-операций на множестве параллельных процессов, например, суммирование элементов распределенного массива. Система времени исполнения MPI сама выбирает порядок выполнения операций, предполагая выполнение свойства ассоциативности, из-за чего ошибки округления меняются от запуска программы к запуску, внося изменения в конечный результат ее работы. Это очень серьезная проблема, которая сегодня встречается часто на системах с массовым параллелизмом и определяет отсутствие повторяемости результатов работы параллельных программ. Данная особенность характерна для второй части AlgoWiki, посвященной реализации алгоритмов, но вопрос очень важный, и соответствующие соображения, по возможности, должны быть отмечены и здесь.

Заметим, что, в некоторых случаях, недетерминированность в структуре алгоритмов можно "убрать" введением соответствующих макроопераций, после чего структура становится не только детерминированной, но и более понятной для восприятия. Подобное действие также следует отразить в данном разделе.

Степень исхода вершины информационного графа показывает, в скольких операциях ее результат будет использоваться в качестве аргумента. Если степень исхода вершины велика, то на этапе реализации алгоритма нужно позаботиться об эффективном доступе к результату ее работы. В этом смысле, особый интерес представляют рассылки данных, когда результат выполнения одной операции используется во многих других вершинах графа, причем число таких вершин растет с увеличением значения внешних переменных.

"Длинные" дуги в информационном графе [1] говорят о потенциальных сложностях с размещением данных в иерархии памяти компьютера на этапе выполнения программы. С одной стороны, длина дуги зависит от выбора конкретной системы координат, в которой расположены вершины графа, а потому в другой системе координат они попросту могут исчезнуть (но не появится ли одновременно других длинных дуг?). А с другой стороны, вне зависимости от системы координат их присутствие может быть сигналом о необходимости длительного хранения данных на определенном уровне иерархии, что накладывает дополнительные ограничения на эффективность реализации алгоритма. Одной из причин возникновения длинных дуг являются рассылки скалярных величин по всем итерациям какого-либо цикла: в таком виде длинные дуги не вызывают каких-либо серьезных проблем на практике.

Для проектирования специализированных процессоров или реализации алгоритма на ПЛИС представляют интерес компактные укладки информационного графа [1], которые также имеет смысл привести в данном разделе.

2 ЧАСТЬ. Программная реализация алгоритма

2.1 Масштабируемость алгоритма и его реализации

Раздел будет добавлен позднее

2.2 Существующие реализации алгоритма

Алгоритм, как и многие другие алгоритмы разбиения графов реализованы в следующих последовательных пакетах декомпозиции графов: METIS, JOSTLE, SCOTCH, CHACO и PARTY. К параллельным пакетам относятся PARMETIS (параллельная версия пакета METIS), JOSTLE, PT-SCOTCH (параллельная версия пакета SCOTCH) и ZOLTAN.

ParMETIS и METIS распространяются свободно URL: http://glaros.dtc.umn.edu/gkhome/software .

ZOLTAN - свободная лицензия, URL: http://www.cs.sandia.gov/~web1400/1400_download.html .

Также алгоритм реализован в параллельном пакете GridSpiderPar, URL: http://lira.imamod.ru/FondProgramm/Decomposition/

3 Литература

[1] Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. - СПб.: БХВ-Петербург, 2002. - 608 с.

[2] Якобовский М.В. Введение в параллельные методы решения задач: Учебное пособие / Предисл.: В. А. Садовничий. – М.: Издательство Московского университета, 2012. – 328 с., илл. – (Серия «Суперкомпьютерное образование»), ISBN 978-5-211-06382-2 URL: http://lira.imamod.ru/ITTPMOPS/

[3] Головченко Е.Н. Параллельный пакет декомпозиции больших сеток // Математическое моделирование. 2011. Т. 23. № 10. 3-18. URL: http://cyberleninka.ru/article/n/razbienie-bolshih-setok

[4] Головченко Е.Н. Декомпозиция расчетных сеток для решения задач механики сплошных сред на высокопроиводительных вычислительных системах. Дисс ... канд. ф.-м.наук. Институт прикладной математики им. М. В. Келдыша РАН, г. Москва URL: http://keldysh.ru/council/3/D00202403/golovchenko_diss.pdf