Участник:Nikmedoed/Нечеткий алгоритм С-средних (Fuzzy C-means)

Данный документ содержит описание схемы, по которой предлагается описывать свойства и структуру каждого алгоритма. Описание состоит из двух частей. В первой части описываются собственно алгоритмы и их свойства, а вторая посвящена описанию особенностей их программной реализации с учетом конкретных программно-аппаратных платформ. Такое деление на части сделано для того, чтобы машинно-независимые свойства алгоритмов, которые определяют качество их реализации на параллельных вычислительных системах, были бы выделены и описаны отдельно от множества вопросов, связанных с последующими этапами программирования алгоритмов и исполнения результирующих программ.

Общая схема описания алгоритмов имеет следующий вид:

1 ЧАСТЬ. Свойства и структура алгоритмов

Свойства алгоритмов никак не зависят от вычислительных систем, и с этой точки зрения данная часть AlgoWiki имеет безусловную собственную ценность. Описание алгоритма делается один раз, после чего многократно используется для его реализации в различных программно-аппаратных средах. Несмотря на то, что в данной части мы рассматриваем лишь машинно-независимые свойства алгоритмов, соображения, важные на этапе реализации, или же ссылки на соответствующие пункты части II AlgoWiki, здесь также вполне уместны.

1.1 Общее описание алгоритма

Алгоритм кластеризации Fuzzy C-Means (FCM) был предложен Дж. Данном в 1973 году и доработан Дж. Бездеком в 1981 году . В отличие от большинства существующих алгоритмов кластеризации, данный алгоритм является нечётким – каждый из объектов не входит однозначно в какой-либо кластер, а принадлежит всем кластерам с различными степенями принадлежности. Это даёт преимущества в качестве разбиения в случаях, когда кластеры находятся близко друг к другу, и большое число точек находится на их границах. Однако ценой такой нечёткости служат большие вычислительные затраты, чем у таких чётких алгоритмов, как Hard C-Means и K-Means, при сохранении таких их недостатков, как априорное определение числа кластеров и отсутствие гарантии глобальной оптимальности результата.

1.2 Математическое описание алгоритма

Исходные данные: массив объектов ${X_k}\in{\R^n}, k=\overline{1,M}$, число кластеров c, экспоненциальный вес $m\in{[1,\infty)}$, параметр останова $\varepsilon\gt 0$. Вычисляемые данные: матрица разбиения $F$ размера $M\times c$ (элементы $\mu_{ki}\in[0,1]$, $\sum^{c}_{i=1} {\mu_{ki}} = 1$), центры кластеров $V_i$, расстояния $D_{ki}$ между объектами и центрами кластеров.

Формулы метода:

$\begin{align} &V_i=\frac{\sum^{M}_{k=1} {\mu^m_{ki} * X_k}}{\sum^{M}_{k=1} {\mu^m_{ki}}},i=\overline{1,c}\\ &D_{ki}=\sqrt{{\lVert X_k - V_i \rVert}^2},k=\overline{1,M},i=\overline{1,c}\\ &\mu_{ki}=\frac{1}{{\left ( \sum^{c}_{j=1} {\frac{D_{ki}}{D_{kj}}} \right ) }^{{2}/{m-1}} },k=\overline{1,M},i=\overline{1,c}\\ \end{align}$

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма Fuzzy C-Means составляют шаги вычисления центров кластеров и расстояний между ними и точками данных, которые требуют порядка $cMn$ операций умножения за итерацию. Также, шаги вычисления центров кластеров и пересчёта матрицы принадлежности требуют по $cM$ операций возведения в степень, что может быть более затратно при малых $n$.

Такое число операций возведения в степень достигается за счёт устранения некоторых повторных вычислений. Так, для шага вычисления центров кластеров величины $\mu_{ki}^m$ могут вычисляться однократно и умножаться на $X_k$ при включении в сумму, записанную в числителе.

На шаге пересчёта матрицы принадлежности нормировочная сумма $\sum^c_{j=1}\frac{1}{D_{kj}}$ может вычисляться однократно для каждого объекта данных и использоваться далее при вычислении всех его степеней принадлежности.

1.4 Макроструктура алгоритма

Алгоритм включает в себя три основных этапа – вычисление центров кластеров, вычисление расстояний между центрами кластеров и точками данных (включающее в себя макрооперации вычитания векторов и вычисления их норм, как правило в Евклидовом пространстве) и пересчёт матрицы принадлежности.

1.5 Схема реализации последовательного алгоритма

Последовательность исполнения алгоритма следующая:

Инициализация происходит случайным заполнением матрицы принадлежности $F$ с соблюдением условия нормировки $\sum_{i=1}^c {\mu_{ki} =1}$ и переходом к шагу 1, либо случайным определением центров кластеров $V_i$ и переходом к шагу 2.

Далее осуществляются итерации следующего вида:

1. $V_i=\frac{\sum_{k=1}^{M} {\mu_{ki}^m * X_k}}{\sum_{k=1}^{M} {\mu_{ki}^m} },i=\overline{1,c}$
2. $D_{ki}=\sqrt{{\lVert X_k - V_i \rVert}^2},k=\overline{1,M},i=\overline{1,c}$
3. $\mu_{ki}=\frac{1}{{\left ( \sum^{c}_{j=1} {\frac{D_{ki}}{D_{kj}}} \right ) }^{{2}/{m-1}} },k=\overline{1,M},i=\overline{1,c}$

В конце каждой итерации проверяется условие останова вида $\max_{k = \overline{1,M},i = \overline{1,c}} {( \left | \mu_{ki} - \mu_{ki}^* \right |)} \lt \varepsilon$, либо $\max_{i = \overline{1,c}} {( \left | V_i - V_i^* \right |)} \lt \varepsilon$, где $\mu_{ki}^* (V_i^*)$ – значение $\mu_{ki}(V_i)$, вычисленное на предыдущей итерации. Если условие не выполнено, осуществляется переход к шагу 1.

1.6 Последовательная сложность алгоритма

При кластеризации $M$ объектов данных, представленных точками в $\R^n$, на $c$ кластеров, алгоритм Fuzzy C-Means в последовательном варианте на каждой итерации производит:

• $cM(n+1)-2c-M$ сложений,
• $cMn$ вычитаний,
• $cM(2n+1)$ умножений,
• $c(M+1)$ делений,
• $2cM$ возведений в степень,
• $cM$ вычислений квадратного корня.

Если считать $n$ малым, то в основную часть алгоритма входят все вышеперечисленные операции, в противном случае – операции сложения, вычитания и умножения. Вычислительная сложность одной итерации алгоритма Fuzzy C-Means – $O(cMn)$.

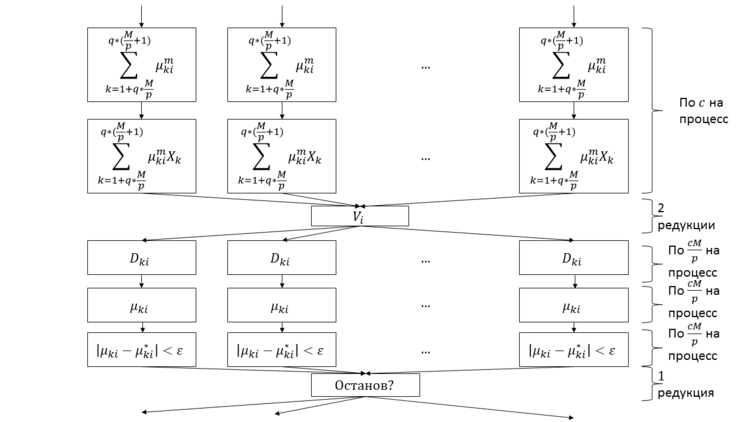
1.7 Информационный граф

Приведём граф единичной итерации алгоритма в параллельном оптимизированном варианте:

Каждая вершина данного графа соответствует операциям из алгоритма, указанным при помощи указанных формул. Каждый из p столбцов соответствует работе одного из процессов. Пометки справа указывают число повторений каждого узла в ходе одной итерации.

Раздел 1.8 уточняет, соответствуют ли эти повторения однотипным ярусам или точкам данных, вычисления для которых можно распараллелить и далее.

Каждый процесс обладает следующими данными:

• координатами точек данных $X_k$, $k=\overline{1+rnk* \frac{M}{p},rnk*(\frac{M}{p}+1)}$, где $rnk$ – номер процесса,
• значениями $\mu_{ki}$ степени принадлежности для своих точек ($k=\overline{1+rnk* \frac{M}{p},rnk*(\frac{M}{p} +1)}, i=\overline{1,c}$),
• координатами центров кластеров $V_i$, $i=\overline{1,c}$.

Суммы $\sum_{k=1+rnk*\frac{M}{p}}^{rnk * ( \frac{M}{p} +1 )} {\mu_{ki}^m}$ и $\sum_{k=1+rnk*\frac{M}{p}}^{rnk * ( \frac{M}{p} +1 )} {\mu_{ki}^m X_k}$ вычисляются одновременно, поэтому значения $\mu_{ki}^m$ вычисляются по одному разу за итерацию. Таким образом, второй ярус операций на рисунке на деле не содержит операций возведения в степень. За счёт линейности большинства выражений относительно данных по точкам, процессы взаимодействуют только при редукции сумм, составляющих $V_i$. Всё остальное время каждый процессор работает только со своими $\frac{M}{p}$ точками. Это обеспечивает применимость алгоритма для больших $M$.

1.8 Ресурс параллелизма алгоритма

При распараллеливании по точкам исходных данных выполнение одной итерации алгоритма FCM может быть разделено на следующие ярусы:

• c ярусов нахождения частичных сумм знаменателя (по $\frac{M}{p}-1$ сложений, $\frac{M}{p}$ операций возведения в степень на процесс),
• c ярусов нахождения частичных сумм числителя (по $\frac{M}{p} -1$ сложений, $\frac{M}{p}$ умножений на процесс),
• c редукций сумм и передач значений $V_i$ процессам,
• c ярусов вычисления расстояний до центров (по $n-1$ сложений, $n$ вычитаний, $n$ умножений, 1 взятие квадратного корня), каждый процесс получает$\frac{M}{p}$ точек на обработку,
• 1 ярус вычислений нормировочных сумм (по $c-1$ сложений, c делений), каждый процесс получает $\frac{M}{p}$ точек на обработку,
• c ярусов вычисления степеней принадлежности точек (по 1 умножению, 1 делению, 1 возведению в степень), каждый процесс получает $\frac{M}{p}$ точек на обработку.

Таким образом, в параллельном варианте при условии наличия в каждом узле достаточного объёма памяти для хранения всего массива координат центров кластеров высота и ширина ЯПФ алгоритма FCM равны соответственно $O(c)$ и $O(Mn)$.

1.9 Входные и выходные данные алгоритма

Входные данные: массив векторов $X_i$, число кластеров $c$, экспоненциальный вес $m\in{[1,\infty)}$, параметр останова $\varepsilon\gt 0$.

Объём входных данных: $Mn$ для входных векторов, 3 вспомогательных параметра.

Выходные данные: матрица принадлежности $F$ (элементы $\mu_{ki}\in[0,1]$). Условие нормировки: $\sum^{c}_{i=1} {\mu_{ki}} = 1$.

Объём выходных данных: $cM$.

1.10 Свойства алгоритма

В случае неограниченного распараллеливания по точкам данных (1 процесс на точку), отношение последовательной сложности алгоритма к параллельной пропорционально $Mn$ (на практике величина $n$ считается малой и не учитывается).

Параметр $m$ задаёт степень «размытости» кластеров. В отсутствие априорных данных его обычно берут равным 2. В предельном случае сведения параметра $m$ к значению 1, кластеры становятся чёткими и алгоритм вырождается в алгоритм кластеризации K-Means.

Алгоритм недетерминирован, начальное положение кластеров задаётся случайно либо явно, либо опосредованно (через матрицу принадлежности). Алгоритм сходится к локальному экстремуму и, таким образом, не гарантирует оптимальный результат при случайном выборе начальных значений.