Thomas algorithm, locality
Основные авторы описания: Вад.В.Воеводин (раздел 2), А.М.Теплов (раздел 3)
Содержание
1 Ссылки
Основной фрагмент реализации, на основе которого были получены количественные оценки, приведен здесь (функция Kernel).
2 Локальность данных и вычислений
Как видно по графу алгоритма, локальность данных по пространству хорошая - все аргументы, которые необходимы для операций, вычисляются "рядом". Однако по времени локальность вычислений не столь хороша. Если данные задачи не помещаются в кэш, то вычисления в "верхнем левом углу" СЛАУ будут выполняться с постоянными промахами кэша. Отсюда может следовать одна из рекомендаций прикладникам, использующим прогонку, - нужно организовать все вычисления так, чтобы прогонки были "достаточно коротки" для помещения данных в кэш.
При этом, однако, прогонка относится к таким последовательным алгоритмам, в которых локальность вычислений настолько велика, что является даже излишней[1]. Из-за того, что данные, необходимые для выполнения основных операций прогонки, вычисляются в непосредственно предшествующим им операциях, возможность использования суперскалярности вычислительных ядер процессоров практически сводится на нет, что резко ухудшает эффективность выполнения прогонки даже на современных однопроцессорных и одноядерных системах.
2.1 Локальность реализации алгоритма
2.1.1 Структура обращений в память и качественная оценка локальности
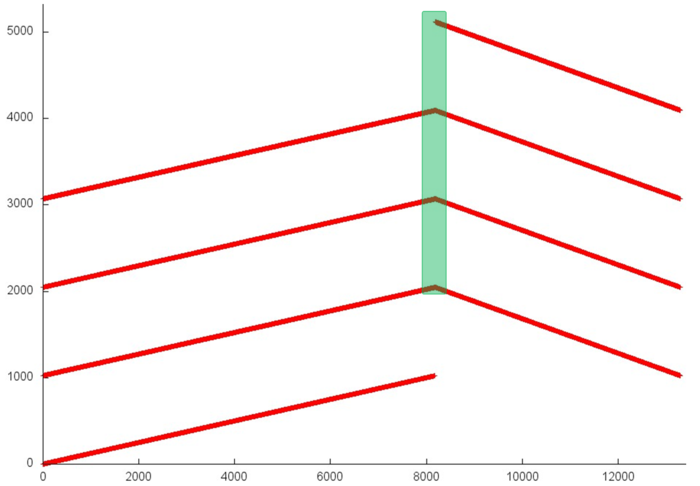
На рис. 1 представлен профиль обращений в память для реализации точечного варианта прогонки. Данный профиль состоит из обращений к 5 массивам – трем диагоналям матрицы, вектору правых частей и результирующему вектору. Исходя из общего профиля, можно увидеть, что программа состоит из двух этапов – на первом выполняется последовательный перебор элементов 4-х массивов, на втором – также последовательный перебор, только в обратном порядке.
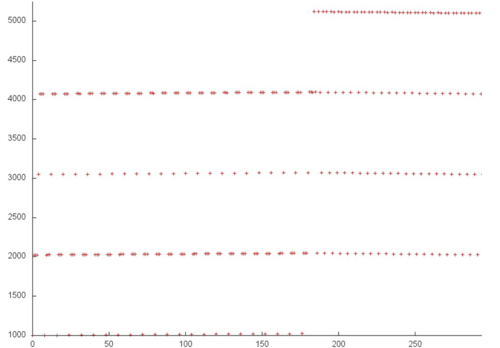
Однако при более детальном рассмотрении можно заметить, что профиль устроен несколько сложнее (рис. 2). Для некоторых массивов на каждом шаге выполняется по несколько очень близких обращений, что приводит к улучшению как пространственной, так и временной локальности.
Таким образом, общий профиль обладает высокой пространственной локальностью (поскольку здесь доминируют последовательные переборы элементов) и средней временной (поскольку некоторые элементы сразу используются повторно).
2.1.2 Количественная оценка локальности
Условия запуска описаны здесь.
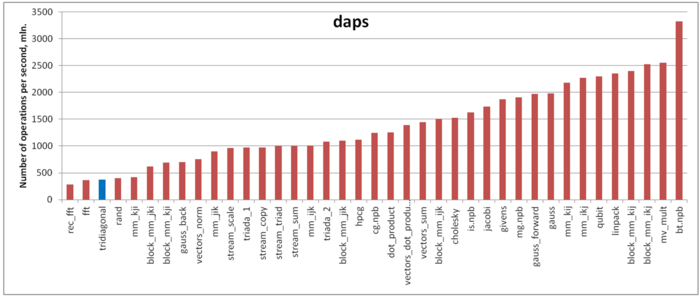
Первая оценка выполняется на основе характеристики daps, которая оценивает число выполненных обращений (чтений и записей) в память в секунду. Данная характеристика является аналогом оценки flops применительно к работе с памятью и является в большей степени оценкой производительности взаимодействия с памятью, чем оценкой локальности. Однако она служит хорошим источником информации, в том числе для сравнения с результатами по следующей характеристике cvg.
На рисунке 3 приведены значения daps для реализаций распространенных алгоритмов, отсортированные по возрастанию (чем больше daps, тем в общем случае выше производительность). Для данной программы значения daps является достаточно неожиданным. Согласно качественному анализу, локальность обращений в память в этом случае достаточно высока. Однако daps оценивает производительность работы с памятью ниже, чем для теста RandomAccess! Такое различие между локальностью и производительностью встречается нечасто.
При детальном рассмотрении исходного кода выяснились две причины такого поведения. Во-первых, итерации основного цикла являются зависимыми по памяти, то есть на очередной итерации используются данные, посчитанные на предыдущей. Похоже, что в данном случае эта зависимость значительно снижает эффективность работы с памятью, в то время как с точки зрения локальности данный случай является достаточно неплохим.
Также выяснилось, что одна из операций деления неожиданно существенно замедляет выполнение программы. При замене этой операции на умножение время выполнения уменьшается в 2.5 раза, при этом ассемблерный код двух вариантов программы выглядел идентично (за исключением очевидной замены одной команды деления на команду умножения).
Такие особенности программы не отражаются в ее свойствах локальности, что и привело к такому существенному разрыву между оценкой локальности и производительностью работы с памятью.
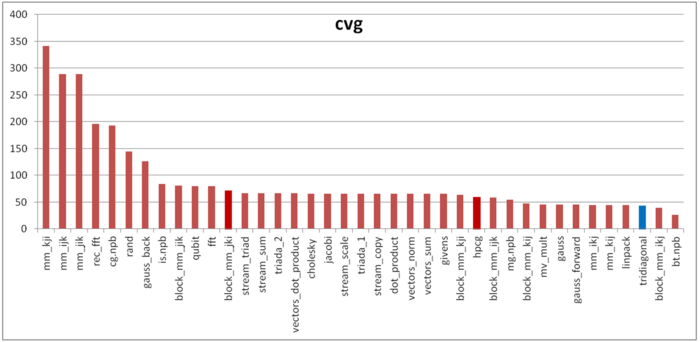
Вторая характеристика – cvg – предназначена для получения более машинно-независимой оценки локальности. Она определяет, насколько часто в программе необходимо подтягивать данные в кэш-память. Соответственно, чем меньше значение cvg, тем реже это нужно делать, и тем лучше локальность алгоритма.
На рисунке 4 приведены значения cvg для того же набора реализаций, отсортированные по убыванию (чем меньше cvg, тем в общем случае выше локальность). В данном случае все предыдущие выводы подтверждаются – локальность оказывается достаточно высокой, что и было замечено согласно качественной оценке локальности.
3 Масштабируемость алгоритма и его реализации
3.1 Масштабируемость алгоритма
О масштабируемости самой прогонки, как полностью непараллельного алгоритма, говорить не имеет смысла. Однако необходимо отметить, что анализ масштабируемости параллельных вариантов прогонки должен проводиться относительно однопроцессорной реализации описанного классического варианта прогонки, а не относительно однопроцессорных расчетов для её параллельных вариантов.
3.2 Масштабируемость реализации алгоритма
Проведём исследование масштабируемости реализации алгоритма согласно методике. Исследование проводилось на суперкомпьютере "Ломоносов"[2] Суперкомпьютерного комплекса Московского университета.
Набор и границы значений изменяемых параметров запуска реализации алгоритма:
- число процессоров 1;
- размер области [10240 : 1024000] с шагом 10240.
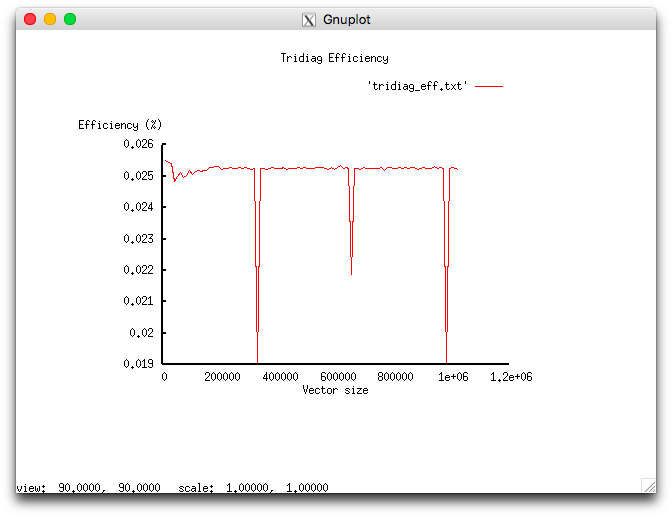
В результате проведенных экспериментов был получен следующий диапазон эффективности реализации алгоритма:
- минимальная эффективность реализации 0.019%;
- максимальная эффективность реализации 0.0255%.
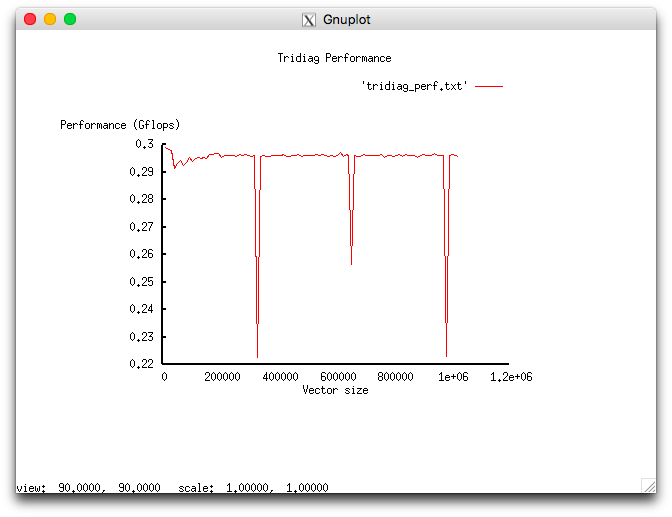
На следующих рисунках приведены графики производительности и эффективности выбранной реализации алгоритма в зависимости от изменяемых параметров запуска.
Малая эффективность, по-видимому, связана с избыточной локальностью, описанной в разделе о локальности данных и вычислений.
4 Динамические характеристики и эффективность реализации алгоритма
В силу существенно последовательной природы алгоритма и его избыточной локальности, исследование его динамических характеристик представляется малоценным.
Все результаты получены на суперкомпьютере "ГрафИТ!". Использовались процессоры Intel Xeon X5570 с пиковой производительностью в 94 Гфлопс, а также компилятор Gnu 4.4.7. На рисунках показана эффективность реализации алгоритма прогонки.
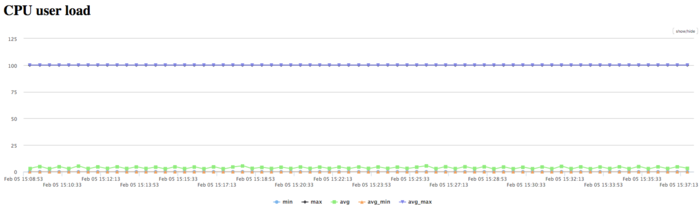
На графике загрузки процессора видно, что почти все время работы программы уровень загрузки составляет около 4% в среднем. Это указывает на достаточно низкую нагрузку выполнения последовательного алгоритма на 8-ми ядерном процессоре.
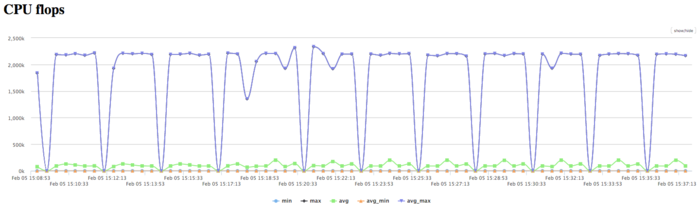
На Рисунке 9 показан график количества операций с плавающей точкой в секунду. На графике видна общая низкая производительность вычислений, достигающая в пике 2,2 млн операций в секунду.
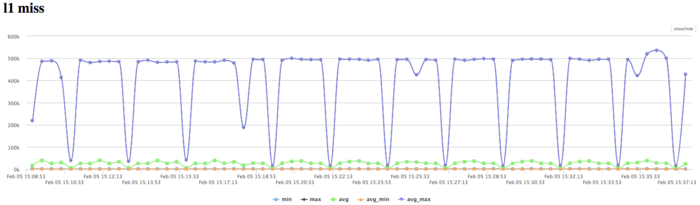
На графике кэш-промахов первого уровня видно, что число промахов достаточно низкое даже для одного ядра и находится на уровне 500 тыс/сек. Это указывает на достаточно хорошую локальность данных.
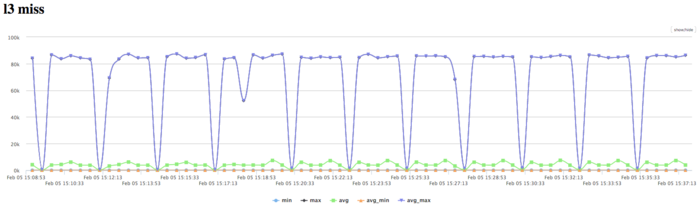
На графике кэш-промахов третьего уровня видно, что число промахов все еще достаточно низкое для небольшого числа процессов и находится на уровне 80 тыс/сек. Отношение промахов L1/L3 около 6, что выше средних показателей по типичным задачам. Это также указывает на хорошую локальность вычислений.
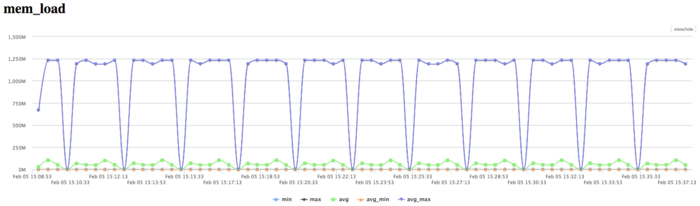
На графике чтений из памяти на наблюдается достаточно высокая активность чтения из памяти процессами. Так как активно работает только один процесс, то и активность чтения соответствует максимальным значениям. Активность достаточно типична для приложений такого класса.
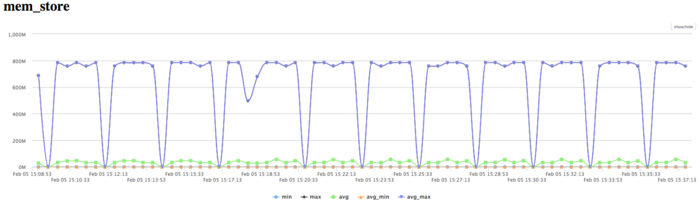
Активность записи в память достаточно низкая, это вполне ожидаемо для такого алгоритма, и так же указывает на достаточно высокую локальность вычислений.
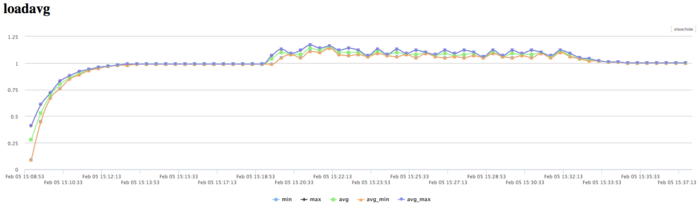
На графике числа процессов, ожидающих вхождения в стадию счета (Loadavg), видно, что на протяжении всей работы программы значение этого параметра постоянно и приблизительно равняется 1. Это свидетельствует о стабильной работе программы с работающим только одним процессом. В целом, по данным системного мониторинга работы программы можно сделать вывод о том, что программа работала не очень эффективно, но с высокой локальностью вычислений. Интенсивность использования памяти низкая, при этом локальность вычислений обеспечивает достаточно эффективное использование кэш-памяти.
5 Результаты прогонов
6 Литература =
- ↑ Фролов А.В., Антонов А.С., Воеводин Вл.В., Теплов А.М. Сопоставление разных методов решения одной задачи по методике проекта Algowiki // Подана на конференцию "Параллельные вычислительные технологии (ПаВТ'2016)".
- ↑ Воеводин Вл., Жуматий С., Соболев С., Антонов А., Брызгалов П., Никитенко Д., Стефанов К., Воеводин Вад. Практика суперкомпьютера «Ломоносов» // Открытые системы, 2012, N 7, С. 36-39.