Алгоритм Тарьяна-Вишкина поиска компонент двусвязности: различия между версиями
| [непроверенная версия] | [непроверенная версия] |
Elijah (обсуждение | вклад) |
Elijah (обсуждение | вклад) |
||
| Строка 75: | Строка 75: | ||
Алгоритм изначально параллельный, время работы <math>O(\ln(|V|))</math> на <math>O(|V| + |E|)</math> процессорах. | Алгоритм изначально параллельный, время работы <math>O(\ln(|V|))</math> на <math>O(|V| + |E|)</math> процессорах. | ||
| − | Изначальные инициализации компонент и уровней вершин [1] и [3] могут выполняться параллельно за <math>O(|V|)</math> операций. Шаг трим [2] так же может быть выполнен за <math>O(|E|)</math> параллельных атомарных операций. Поиски в ширину от каждой корневой вершины [4],[BFS] производятся последовательно друг за другом, однако сами поиски в ширину обладают значительным образом параллелизма, описанным в соответствующем [[Поиск_в_ширину_(BFS)|разделе]]. | + | Изначальные инициализации компонент и уровней вершин [1] и [3] могут выполняться параллельно за <math>O(|V|)</math> операций. Шаг трим [2] так же может быть выполнен за <math>O(|E|)</math> параллельных атомарных операций. Поиски в ширину от каждой корневой вершины [4],[BFS] производятся последовательно друг за другом, однако сами поиски в ширину обладают значительным образом параллелизма, описанным в соответствующем [[Поиск_в_ширину_(BFS)|разделе]]. |
| + | |||
| + | Нумерация вершин <math>D(v)</math> в порядке обходе графа поиском в глубину [5],[6] должно выполняться сугубо последовательно за <math>O(|V|)</math> операций, и может, вообще говоря, серьезно снизить производительность реализации на параллельных архитектурах. | ||
| + | |||
| + | Вычисление величин <math>L</math>, <math>H</math> и ребер, являющихся мостами [8],[9],[10] может выполняться каждое за <math>O(|V|)</math> операций. | ||
| + | |||
| + | Таким образом, ширина ярусно-параллельной формы алгоритма равна <math>O(|E|)</math>, а высота ЯПФ, вообще говоря, зависит от структуры входного графа (числа связанных компонент, и, как следствие, числа необходимых поисков в ширину). | ||
=== Входные и выходные данные алгоритма === | === Входные и выходные данные алгоритма === | ||
Версия 17:07, 15 августа 2017
| Алгоритм Тарьяна-Вишкина поиска компонент двусвязности/мостов в графе | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]O(|V| + |E|)[/math] |
| Объём входных данных | [math]O(|V| + |E|)[/math] |
| Объём выходных данных | [math]max O(|V|)[/math] |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math]N/A [/math] |
| Ширина ярусно-параллельной формы | [math] O(|V|) [/math] |
Основные авторы описания: И.В.Афанасьев
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Параллельный алгоритм Тарьяна-Вишкина [1] находит компоненты двухсвязности неориентированного графа за время [math]O(\ln |V|)[/math] на [math]O(|V| + |E|)[/math] процессорах. Алгоритм может быть адаптирован для поиска мостов. Эффективность алгоритма Тарьяна-Вишкина подтверждена в последнее время[2][3] как на системах архитектуры SMP, так и при вычислениях на GPU.
1.2 Математическое описание алгоритма
1. Для каждой компоненты связности графа найти какое-либо остовное дерево [math]T[/math].
2. Перенумеровать вершины [math]T[/math] в порядке обратного обхода.
3. В порядке возрастания номера вершины выполнить следующие действия:
a. [math]D(v) := 1+ \sum_{v \rightarrow w}D(w) [/math]
b. [math] L(v) := \min { \{N(v) - D(v)+1 \} \cup \{ L(w) | v \rightarrow w \} \cup \{ N(w) | v \cdots w \} }[/math]
c. [math] H(v) := \max { \{ N(v) \} \cup \{ H(w) | v \rightarrow w \} \cup \{ N(w) | v \cdots w \} }[/math]
d. Пометить ребро [math]v \rightarrow w[/math] мостом, если [math]H(w)\lt =N(w)[/math] и [math]L(w)\gt N(w)-D(w)[/math].
1.3 Вычислительное ядро алгоритма
Вычислительно затратной частью алгоритма является поиск в ширину, вычисляющий величины [math]N(v)[/math], вычислительным ядром которого является обход вершин, смежной к выбранной вершине [math]v[/math] с последующем добавлением еще не посещенных вершин в множество [math]P[/math]. Данная операция выполняться на каждом шаге для каждой вершины [math]v[/math] графа.
1.4 Макроструктура алгоритма
На первом шаге работы алгоритма строится остовный лес графа с использованием модифицированного алгоритма Шилоаха-Вишкина.
Для этого для каждой вершины [math]v[/math] определяется указатель на родительскую вершину [math]P(v)[/math]; на шаге инициализации [math]P(v):=v[/math]. Далее остовный лес строится чередованием двух параллельных операций:
• Удвоение указателей: [math]P(v):=P(P(v))[/math] ;
• Соединение: [math]P(P(v)):=P(w)[/math], где [math]v[/math] – вершина [math]P[/math]-дерева ( [math]P(v)=v[/math]на текущем шаге), [math]w[/math]– некоторая вершина, для которой существует ребро [math](v,w)\in E[/math]. Ребро помечается, как принадлежащее остовному лесу .
Далее производятся следующие шаги:
• перенумерация вершин в обратном порядке обхода (post-order);
• вычисление количества потомков [math]D(v)[/math] для каждой вершины;
• вычисление значений [math]L(v)[/math] и [math]H(v)[/math] для каждой вершины;
• пометка рёбер [math]v \rightarrow w[/math] мостами, если [math]H(w)\lt =N(w)[/math] и [math]L(w)\gt N(w)-D(w)[/math].
Основной идеей для обеспечения завершения работы алгоритма за [math]O( \ln |V|)[/math] шагов является систематическое использование операции удвоения указателей.
1.5 Схема реализации последовательного алгоритма
1.6 Последовательная сложность алгоритма
Последовательный вариант алгоритма аналогичен алгоритму Тарьяна[4] и имеет линейную сложность [math]O(|E| + |V|)[/math].
1.7 Информационный граф
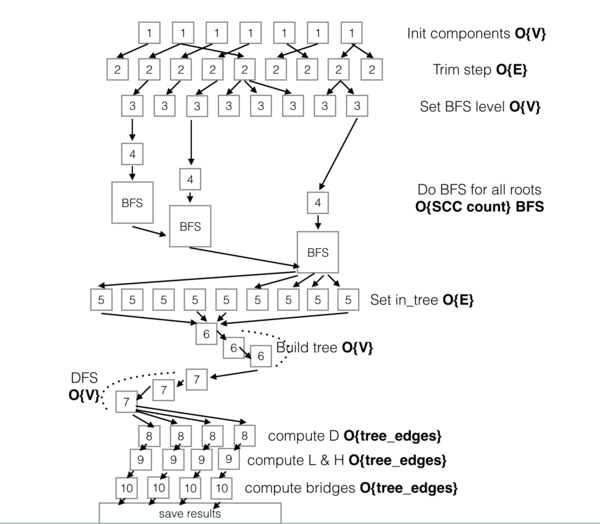
Далее на рисунке 1 представлен информационный граф алгоритма, демонстрирующий его основные уровни параллелизма.
В начале работы производится инциализация связанных компонент графа [1] и выделение тривиальных компонент (размера 1 и 2) [2], затем инициализация уровней для всех вершин [3] и последовательные поиски в ширину [4],[BFS] до тех пор, пока все вершины не будут размечены различными уровнями.
Далее происходит поиск ребер, которые войдут в остовное дерево [5] и последовательное построение данного дерева на основе поиска в глубину [6],[7]. Затем друг за другом вычисляются необходимые метрики для каждой их вершин L, H и D [8],[9]. В конце на основе данных метрик вычисляются мосты в графе [10].
1.8 Ресурс параллелизма алгоритма
Алгоритм изначально параллельный, время работы [math]O(\ln(|V|))[/math] на [math]O(|V| + |E|)[/math] процессорах.
Изначальные инициализации компонент и уровней вершин [1] и [3] могут выполняться параллельно за [math]O(|V|)[/math] операций. Шаг трим [2] так же может быть выполнен за [math]O(|E|)[/math] параллельных атомарных операций. Поиски в ширину от каждой корневой вершины [4],[BFS] производятся последовательно друг за другом, однако сами поиски в ширину обладают значительным образом параллелизма, описанным в соответствующем разделе.
Нумерация вершин [math]D(v)[/math] в порядке обходе графа поиском в глубину [5],[6] должно выполняться сугубо последовательно за [math]O(|V|)[/math] операций, и может, вообще говоря, серьезно снизить производительность реализации на параллельных архитектурах.
Вычисление величин [math]L[/math], [math]H[/math] и ребер, являющихся мостами [8],[9],[10] может выполняться каждое за [math]O(|V|)[/math] операций.
Таким образом, ширина ярусно-параллельной формы алгоритма равна [math]O(|E|)[/math], а высота ЯПФ, вообще говоря, зависит от структуры входного графа (числа связанных компонент, и, как следствие, числа необходимых поисков в ширину).
1.9 Входные и выходные данные алгоритма
Входные данные: граф [math]G(V, E)[/math], [math]|V|[/math] вершин [math]v_i[/math] и [math]|E|[/math] рёбер [math]e_j = (v^{(1)}_{j}, v^{(2)}_{j})[/math].
Объём входных данных: [math]O(|V| + |E|)[/math].
Выходные данные
Список ребер, являющихся мостами в графе.
Объём выходных данных:
1. [math]O(|E|)[/math] в случае хранения массива принадлежности каждого ребра к множеству мостов в графе
2. [math]max O(|V|)[/math] в случае хранения мостов в виде списка пар вершин
1.10 Свойства алгоритма
1. Компонента сильной связности – подграф, любые две вершины которого принадлежат какому-либо циклу, и содержащий все такие циклы для своих вершин.
2. Компонента сильной связности является объединением всех циклом, проходящих через её вершины.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.2.1 Локальность реализации алгоритма
2.2.1.1 Структура обращений в память и качественная оценка локальности
2.2.1.2 Количественная оценка локальности
2.3 Возможные способы и особенности параллельной реализации алгоритма
Программа, реализующая алгоритм Тарьяна-Вышкина, состоит из двух частей: CPU части, отвечающей за параллельные вычисления на многоядерных CPU, а так же копирование данных на GPU и общее управлениями вычислениями, и GPU части, отвечающей только за вычисления на графическом ускорителе.
2.4 Масштабируемость алгоритма и его реализации
2.4.1 Масштабируемость алгоритма
2.4.2 Масштабируемость реализации алгоритма
Проведём исследование масштабируемости параллельной реализации алгоритма Тарьяна-Вишкина согласно методике. Исследование проводилось на суперкомпьютере "Ломоносов-2 Суперкомпьютерного комплекса Московского университета.
Набор и границы значений изменяемых параметров запуска реализации алгоритма:
- размер графа [2^18 : 2^26].
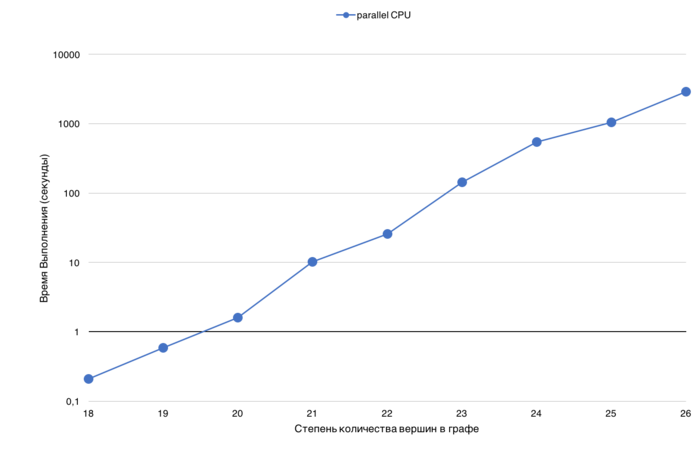
Проведем отдельные исследования масштабируемости вширь реализации алгоритма Тарьяна-Вишкина.
Основной характеристикой для сравнения было выбрано время выполнения, так как производительность (определения как TEPS то есть число ребер графа, которое алгоритм обрабатывает в секунду) для данной операции не отражает реальную эффективность обработки.
Анализируя время выполнения можно оценить, насколько понижается эффективность обработки графа при увеличении его размера (данные перестают помещаться в кэш, в память GPU, узла и т.д.).
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
3 Литература
- ↑ Tarjan, Robert Endre, and Uzi Vishkin. “An Efficient Parallel Biconnectivity Algorithm.” SIAM Journal on Computing 14, no. 4 (1985): 862–74.
- ↑ Edwards, James A, and Uzi Vishkin. “Better Speedups Using Simpler Parallel Programming for Graph Connectivity and Biconnectivity,” PMAM’12, 103–114, New York, USA: ACM Press, 2012. doi:10.1145/2141702.2141714
- ↑ Guojing Cong, and David A Bader. “An Experimental Study of Parallel Biconnected Components Algorithms on Symmetric Multiprocessors (SMPs),” 45b, IEEE, 2005. doi:10.1109/IPDPS.2005.100.
- ↑ Tarjan, Robert. “Depth-First Search and Linear Graph Algorithms.” SIAM Journal on Computing 1, no. 2 (1972): 146–60.