Встречная прогонка, точечный вариант: различия между версиями
| [непроверенная версия] | [непроверенная версия] |
Frolov (обсуждение | вклад) |
Frolov (обсуждение | вклад) м |
||
| Строка 1: | Строка 1: | ||
{{algorithm | {{algorithm | ||
| name = Прогонка для трёхдиагональной матрицы,<br /> точечный вариант | | name = Прогонка для трёхдиагональной матрицы,<br /> точечный вариант | ||
| − | | serial_complexity = <math>8n- | + | | serial_complexity = <math>8n-2</math> |
| pf_height = <math>2.5n+3</math> | | pf_height = <math>2.5n+3</math> | ||
| pf_width = <math>4</math> | | pf_width = <math>4</math> | ||
| Строка 67: | Строка 67: | ||
'''Встречная прогонка''', как и [[Прогонка, точечный вариант|классическая монотонная]], заключается в исключении из уравнений неизвестных, однако, в отличие от монотонной, в ней исключение ведут одновременно с обоих "краёв" СЛАУ (верхнего и нижнего). | '''Встречная прогонка''', как и [[Прогонка, точечный вариант|классическая монотонная]], заключается в исключении из уравнений неизвестных, однако, в отличие от монотонной, в ней исключение ведут одновременно с обоих "краёв" СЛАУ (верхнего и нижнего). | ||
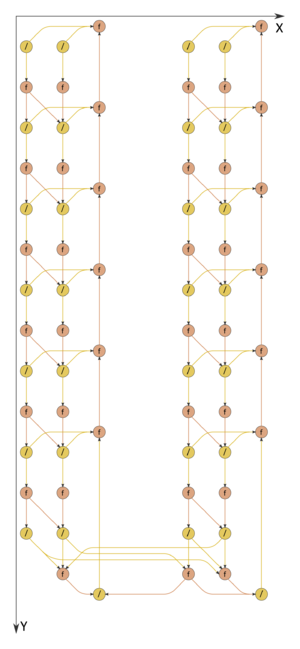
| − | [[file:VstrProgonka.png|thumb|right|300px|Рисунок 1. Граф алгоритма прогонки при n= | + | [[file:VstrProgonka.png|thumb|right|300px|Рисунок 1. Граф алгоритма прогонки при n=14 без отображения входных и выходных данных. '''/''' - деление, '''''f''''' - операция '''''a+bc''''' или '''''a-bc'''''.]] |
=== Математическое описание алгоритма === | === Математическое описание алгоритма === | ||
| Строка 99: | Строка 99: | ||
y_{i+1} = \xi_{i+1} y_{i} + \eta_{i+1}, \quad i = m, m+1, \cdots , N-1. | y_{i+1} = \xi_{i+1} y_{i} + \eta_{i+1}, \quad i = m, m+1, \cdots , N-1. | ||
</math> | </math> | ||
| + | |||
| + | В обычно приводимых<ref name="SETKI" /> формулах встречной прогонки нет формулы для <math>y_{m-1}</math>, который вычисляется затем в обратном ходе. Однако это удлиняет критический путь графа, откладывая вычисление <math>y_{m-1}</math> на момент, когда уже будет вычислен <math>y_{m}</math>, хотя они могут вычисляться одновременно почти независимо друг от друга. | ||
=== Вычислительное ядро алгоритма === | === Вычислительное ядро алгоритма === | ||
| Строка 150: | Строка 152: | ||
Для выполнения встречной прогонки в трёхдиагональной СЛАУ из n уравнений с n неизвестными в последовательном (наиболее быстром) варианте требуется: | Для выполнения встречной прогонки в трёхдиагональной СЛАУ из n уравнений с n неизвестными в последовательном (наиболее быстром) варианте требуется: | ||
| − | * <math>2n+ | + | * <math>2n+2</math> делений, |
| − | * <math>3n- | + | * <math>3n-2</math> сложений/вычитаний, |
| − | * <math>3n- | + | * <math>3n-2</math> умножений. |
При классификации по последовательной сложности, таким образом, прогонка относится к алгоритмам ''с линейной сложностью''. | При классификации по последовательной сложности, таким образом, прогонка относится к алгоритмам ''с линейной сложностью''. | ||
Версия 16:24, 25 ноября 2015
| Прогонка для трёхдиагональной матрицы, точечный вариант | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]8n-2[/math] |
| Объём входных данных | [math]4n-2[/math] |
| Объём выходных данных | [math]n[/math] |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math]2.5n+3[/math] |
| Ширина ярусно-параллельной формы | [math]4[/math] |
Основные авторы описания: А.В.Фролов
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Описание ресурса параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Встречная прогонка - один из вариантов метода исключения неизвестных в приложении к решению СЛАУ[1][2] вида [math]Ax = b[/math], где
- [math] A = \begin{bmatrix} a_{11} & a_{12} & 0 & \cdots & \cdots & 0 \\ a_{21} & a_{22} & a_{23}& \cdots & \cdots & 0 \\ 0 & a_{32} & a_{33} & \cdots & \cdots & 0 \\ \vdots & \vdots & \ddots & \ddots & \ddots & 0 \\ 0 & \cdots & \cdots & a_{n-1 n-2} & a_{n-1 n-1} & a_{n-1 n} \\ 0 & \cdots & \cdots & 0 & a_{n n-1} & a_{n n} \\ \end{bmatrix}, x = \begin{bmatrix} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \\ \end{bmatrix}, b = \begin{bmatrix} b_{1} \\ b_{2} \\ \vdots \\ b_{n} \\ \end{bmatrix} [/math]
Часто, однако, при изложении сути метода прогонки[3] элементы правой части и матрицы системы обозначают и нумеруют по-другому, например СЛАУ может иметь вид ([math]N=n-1[/math])
- [math] A = \begin{bmatrix} c_{0} & -b_{0} & 0 & \cdots & \cdots & 0 \\ -a_{1} & c_{1} & -b_{1} & \cdots & \cdots & 0 \\ 0 & -a_{2} & c_{2} & \cdots & \cdots & 0 \\ \vdots & \vdots & \ddots & \ddots & \ddots & 0 \\ 0 & \cdots & \cdots & -a_{N-1} & c_{N-1} & -b_{N-1} \\ 0 & \cdots & \cdots & 0 & -a_{N} & c_{N} \\ \end{bmatrix}\begin{bmatrix} y_{0} \\ y_{1} \\ \vdots \\ y_{N} \\ \end{bmatrix} = \begin{bmatrix} f_{0} \\ f_{1} \\ \vdots \\ f_{N} \\ \end{bmatrix} [/math]
или, если записывать отдельно по уравнениям, то
- [math] c_{0} y_{0} - b_{0} y_{1} = f_{0},\\ -a_{i} y_{i-1} + c_{i} y_{i} - b_{i} y_{i+1} = f_{i}, 1 \le i \le N-1, \\ -a_{N} y_{N-1} + c_{N} y_{N} = f_{N} [/math]
Встречная прогонка, как и классическая монотонная, заключается в исключении из уравнений неизвестных, однако, в отличие от монотонной, в ней исключение ведут одновременно с обоих "краёв" СЛАУ (верхнего и нижнего).
1.2 Математическое описание алгоритма
[math]m[/math] - номер уравнения, на котором "встречаются" две ветви прямого хода - "сверху" и "снизу".
В приведённых обозначениях во встречной прогонке сначала выполняют её прямой ход - вычисляют коэффициенты
"сверху":
- [math] \alpha_{1} = b_{0}/c_{0},\\ \beta_{1} = f_{0}/c_{0}, \\ \alpha_{i+1} = b_{i}/(c_{i}-a_{i}\alpha_{i}), \quad i = 1, 2, \cdots , m-1, \\ \beta_{i+1} = (f_{i}+a_{i}\beta_{i})/(c_{i}-a_{i}\alpha_{i}), \quad i = 1, 2, \cdots , m-1. [/math]
и "снизу":
- [math] \xi_{N} = a_{N}/c_{N},\\ \eta_{1} = f_{N}/c_{N}, \\ \xi_{i} = a_{i}/(c_{i}-b_{i}\xi_{i+1}), \quad i = N-1, N-2, \cdots , m, \\ \eta_{i} = (f_{i}+b_{i}\eta_{i+1})/(c_{i}-b_{i}\xi_{i+1}), \quad i = N-1, N-2, \cdots , m. [/math]
после чего вычисляют решение с помощью обратного хода
- [math] y_{m} = (\eta_{m}+\xi_{m}\beta_{m})/(1-\xi_{m}\alpha_{m}), \\ y_{m-1} = (\beta_{m}+\alpha_{m}\eta_{m})/(1-\xi_{m}\alpha_{m}), \\ y_{i} = \alpha_{i+1} y_{i+1} + \beta_{i+1}, \quad i = m-2, \cdots , 1, 0, \\ y_{i+1} = \xi_{i+1} y_{i} + \eta_{i+1}, \quad i = m, m+1, \cdots , N-1. [/math]
В обычно приводимых[3] формулах встречной прогонки нет формулы для [math]y_{m-1}[/math], который вычисляется затем в обратном ходе. Однако это удлиняет критический путь графа, откладывая вычисление [math]y_{m-1}[/math] на момент, когда уже будет вычислен [math]y_{m}[/math], хотя они могут вычисляться одновременно почти независимо друг от друга.
1.3 Вычислительное ядро алгоритма
Вычислительное ядро алгоритма можно, как и для классической монотонной прогонки, представить из двух частей - прямого и обратного хода, однако их ширина вдвое больше, чем в монотонном случае. В прямом ходе ядро составляют две независимые последовательности операций деления, умножения и сложения/вычитания. В обратном ходе в ядре остаются только две независимые последовательности умножения и сложения.
1.4 Макроструктура алгоритма
Кроме представления макроструктуры алгоритма как совокупности прямого и обратного хода, прямой ход также может быть разложен на две макроединицы - прямой ход правой и левой прогонок, выполняемых для разных половин СЛАУ, которые выполняются "одновременно", т.е., параллельно друг другу. Обратный ход также может быть разложен на две макроединицы - обратный ход правой и левой прогонок, выполняемых для разных половин СЛАУ, которые выполняются "одновременно", т.е., параллельно друг другу.
1.5 Схема реализации последовательного алгоритма
Последовательность исполнения метода следующая:
1. Инициализируется прямой ход:
- [math] \alpha_{1} = b_{0}/c_{0},\\ \beta_{1} = f_{0}/c_{0}, \\ \xi_{N} = a_{N}/c_{N},\\ \eta_{1} = f_{N}/c_{N}. [/math]
2. Последовательно выполняются формулы прямого хода:
- [math] \alpha_{i+1} = b_{i}/(c_{i}-a_{i}\alpha_{i}), \quad i = 1, 2, \cdots , m-1, \\ \beta_{i+1} = (f_{i}+a_{i}\beta_{i})/(c_{i}-a_{i}\alpha_{i}), \quad i = 1, 2, \cdots , m-1, \\ \xi_{i} = a_{i}/(c_{i}-b_{i}\xi_{i+1}), \quad i = N-1, N-2, \cdots , m, \\ \eta_{i} = (f_{i}+b_{i}\eta_{i+1})/(c_{i}-b_{i}\xi_{i+1}), \quad i = N-1, N-2, \cdots , m. [/math]
3. Инициализируется обратный ход:
- [math] y_{m-1} = (\beta_{m}+\alpha_{m}\eta_{m})/(1-\xi_{m}\alpha_{m}), \\ y_{m} = (\eta_{m}+\xi_{m}\beta_{m})/(1-\xi_{m}\alpha_{m}). [/math]
4. Последовательно выполняются формулы обратного хода:
- [math] y_{i} = \alpha_{i+1} y_{i+1} + \beta_{i+1}, \quad i = m-1, m-2, \cdots , 1, 0, \\ y_{i+1} = \xi_{i+1} y_{i} + \eta_{i+1}, \quad i = m, m+1, \cdots , N-1. [/math]
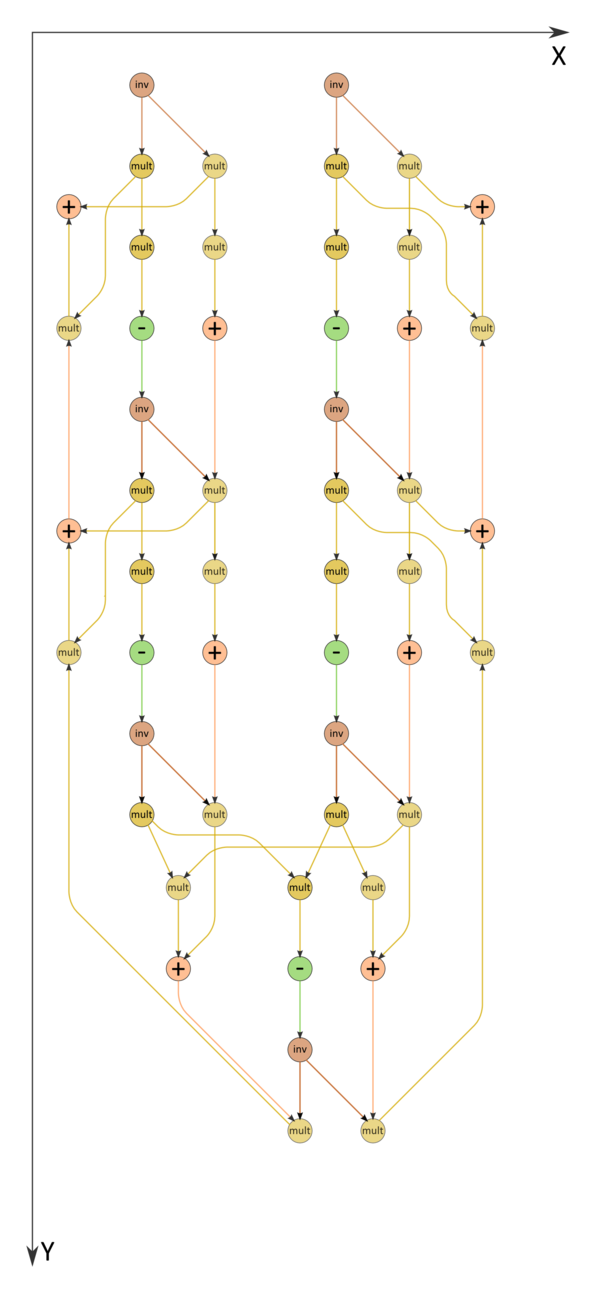
В связи с тем, что почти во всех формулах есть пары делений на одно и то же выражение, можно поменять их на последовательности вычисления обратных чисел с последующими умножениями на ниx (см. Рисунок 2)
1.6 Последовательная сложность алгоритма
Для выполнения встречной прогонки в трёхдиагональной СЛАУ из n уравнений с n неизвестными в последовательном (наиболее быстром) варианте требуется:
- [math]2n+2[/math] делений,
- [math]3n-2[/math] сложений/вычитаний,
- [math]3n-2[/math] умножений.
При классификации по последовательной сложности, таким образом, прогонка относится к алгоритмам с линейной сложностью.
1.7 Информационный граф
1.8 Описание ресурса параллелизма алгоритма
Обе ветви прямого хода выполняются одновременно для [math]N=2m-1[/math], т.е. для [math]n=2m[/math]. Тогда для выполнения встречной прогонки требуется последовательно выполнить следующие ярусы:
- [math]m+1[/math] ярусов делений (в каждом из ярусов, кроме одного, по 4 деления),
- по [math]2m+1[/math] ярусов умножений и сложений/вычитаний (в [math]m-1[/math] ярусах - по 4 операции, в [math]m-1[/math] - по две, в одном - по одной).
При классификации по высоте ЯПФ, таким образом, прогонка относится к алгоритмам со сложностью [math]O(n)[/math]. При классификации по ширине ЯПФ его сложность будет равна [math]4[/math].
1.9 Входные и выходные данные алгоритма
Входные данные: трёхдиагональная матрица [math]A[/math] (элементы [math]a_{ij}[/math]), вектор [math]b[/math] (элементы [math]b_{i}[/math]).
Выходные данные: вектор [math]x[/math] (элементы [math]x_{i}[/math]).
Объём выходных данных: [math]n[/math].
1.10 Свойства алгоритма
Соотношение последовательной и параллельной сложности, как хорошо видно, является константой (причём менее 4).
При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных – тоже константа.
Алгоритм в рамках выбранной версии полностью детерминирован.
Обычно встречная прогонка, как и монотонная, используется для решения СЛАУ с диагональным преобладанием. Тогда гарантируется устойчивость алгоритма. В случае, когда требуется решение нескольких СЛАУ с одной и той же матрицей, ветви вычислений с нахождением коэффициентов можно не повторять. Тогда предпочтителен вариант с заменой делений.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
В зависимости от нужд вычислений, возможны как разные способы хранения матрицы СЛАУ (в виде одного массива с 3 строками или в виде 3 разных массивов), так и разные способы хранения вычисляемых коэффициентов (на месте использованных уже элементов матрицы либо отдельно).
2.2 Локальность данных и вычислений
Как видно по графу алгоритма, локальность данных по пространству хорошая - все аргументы, что нужны операциям, вычисляются "рядом". Однако по времени локальность вычислений не столь хороша. Если данные задачи не помещаются в кэш, то вычисления в "верхнем левом" и "нижнем правом" "углах" СЛАУ будут выполняться с постоянными промахами кэша. Отсюда может следовать одна из рекомендаций прикладникам, использующим прогонку, - нужно организовать все вычисления так, что бы прогонки были "достаточно коротки" для помещения данных в кэш.
2.3 Возможные способы и особенности параллельной реализации алгоритма
Встречная прогонка задумана изначально для случая, когда нужно найти только какую-то близкую к "середине" компоненту вектора решения, а остальные были не нужны (решение т.н. "частичной задачи"). При появлении параллельных компьютерных устройств оказалось, что у встречной прогонки есть небольшой ресурс параллелизма, и она убыстряет счёт, если её верхнюю и нижнюю ветви раскидать на 2 процессора. Однако для получения массового параллелизма встречная прогонка непригодна из-за низкой ширины своей ЯПФ (равной 4 на прямом и 2 - на обратном ходе).
2.4 Масштабируемость алгоритма и его реализации
О масштабируемости самой встречной прогонки, как почти непараллельного алгоритма, говорить нельзя в принципе, за исключением разве что двухпроцессорных систем.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
Встречная прогонка - метод для архитектуры классического, фон-неймановского типа. Для распараллеливания решения СЛАУ с трёхдиагональной матрицей следует взять какой-либо её параллельный заменитель, например, наиболее распространённую циклическую редукцию, или уступающий ей по критическому пути графа, но имеющий более регулярную структуру графа новый последовательно-параллельный метод.