Простой алгоритм Кули-Тьюки быстрого преобразования Фурье для степеней двойки

Простой алгоритм Кули-Тьюки
Последовательный алгоритм
Последовательная сложность	[math]O (n log_{2} n)[/math]
Объём входных данных	[math]n[/math]
Объём выходных данных	[math]n[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]O (log_{2} n)[/math]
Ширина ярусно-параллельной формы	[math]n[/math]

Основные авторы описания: А.В.Фролов, Вад.В.Воеводин (раздел 2.2)

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Простой алгоритм Кули-Тьюки - один из вариантов быстрого преобразования Фурье для комплексных векторов с размерностью, равной степени двойки, без использования специфичных приёмов, использующихся для степеней четвёрки, восьмёрки и др. Заключается в последовательном применении метода быстрого преобразования Фурье и сведении преобразования к последовательности преобразований Фурье размерности 2 и выполнения умножений на т.н. поворотные множители. Несмотря на то, что проигрывает алгоритмам Кули-Тьюки, разлагающим степени двойки на степени 4, 8 и др. и использующим их специфику, весьма распространён, что связано с самой простой из алгоритмов БПФ записью программной реализации.

1.2 Математическое описание алгоритма

Исходные данные: преобразуемый комплексный вектор [math]a[/math] (элементы [math]a_{i}[/math]).

Вычисляемые данные: комплексный вектор - результат преобразования [math]b[/math] (элементы [math]b_{i}[/math]).

При этом размерность векторов - [math]n[/math], причём [math]n = 2^l[/math]

1.2.1 Рекурсивное описание

Вектор записывается по строкам по 2 элемента в каждой. После этого над каждой строкой выполняется преобразование Фурье порядка 2, получившиеся элементы умножаются на поворотные множители [math]exp (2 \pi i(m-1)(j-1)/n)[/math] ([math]m[/math] - номер строки, [math]j[/math] - номер столбца), после чего выполняется БПФ порядка [math]n/2[/math] над каждым из столбцов. Поскольку для 1-го столбца поворотные множители равны 1, то реально умножение на них не выполняется, а умножения на поворотные множители элементов второго столбца соединяются с преобразованием Фурье порядка 2. Эта комбинация, называемая "бабочкой" в среде специалистов по БПФ, и является основной операцией в простом алгоритме Кули-Тьюки. "Бабочка" состоит из вычисления суммы двух комплексных чисел, а также из вычисления их разности с последующим умножением на комплексное число. Всего на каждом шаге выполняется [math]n/2[/math] "бабочек", а шагов - [math]l-1[/math]. Последний, [math]l[/math]-й шаг вычисляет только суммы и разности.

1.2.2 Тригонометрические функции

Несмотря на то, что в вычислениях используются поворотные множители [math]exp (2 \pi i(m-1)(j-1)/n)[/math], нецелесообразно вычислять их в процессе выполнения алгоритма Кули-Тьюки, поскольку вычисления косинусов и синусов (в мнимой экспоненте) тогда составили бы львиную долю вычислений алгоритма. Поэтому обычно (как и в других версиях БПФ) поворотные множители вычисляются заранее и хранятся в специальном массиве. Здесь мы будем предполагать, что алгоритм выполняется именно так.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма составляют "бабочки", состоящие из вычисления суммы двух комплексных чисел, а также из вычисления их разности с последующим умножением на комплексное число. Всего их [math](1/2) n log_{2} n [/math] штук, при этом в [math]n/2[/math] из них умножение не выполняется.

1.4 Макроструктура алгоритма

Макроструктура алгоритма лучше всего описывается рекурсивно, как [math]n/2[/math] преобразований Фурье порядка 2, умножение [math]n/2[/math] пар комплексных чисел и затем 2 БПФ порядка [math]n/2[/math].

1.5 Схема реализации последовательного алгоритма

Нерекурсивная схема организации состоит в том, что на каждом шаге (а всего их [math]log_{2} n [/math]) для выполнения "бабочки" все элементы разбиваются на [math]n/2[/math] пар. В зависимости от номера шага, разница координат для каждой пары элементов удваивается. На первом шагу она равна 1, на последнем - [math]n/2[/math]. При этом результат суммы записывается в элемент с меньшим номером, а результат вычитания с последующим умножением - в элемент с большим.

1.6 Последовательная сложность алгоритма

Если считать только главные члены выражений для последовательной сложности алгоритма, то простой алгоритм Кули-Тьюки может быть выполнен за [math]n log_{2} n[/math] операций комплексного сложения и [math](1/2) n log_{2} n [/math]операций комплексного умножения. Таким образом, простой алгоритм Кули-Тьюки может быть отнесён к линейно-логарифмическому классу по последовательной сложности.

1.7 Информационный граф

Рисунок 1. Простой алгоритм Кули-Тьюки для n=8. Op+ - операция сложения двух комплексных чисел. Op- - операция вычитания двух комплексных чисел и умножения результата вычитания на комплексное число (поворотный множитель). В последнем столбце операций умножение не производится. Привязка вершин выполнена по оси абсцисс - к параметру внешнего цикла, по оси ординат - к обрабатываемым элементам массива

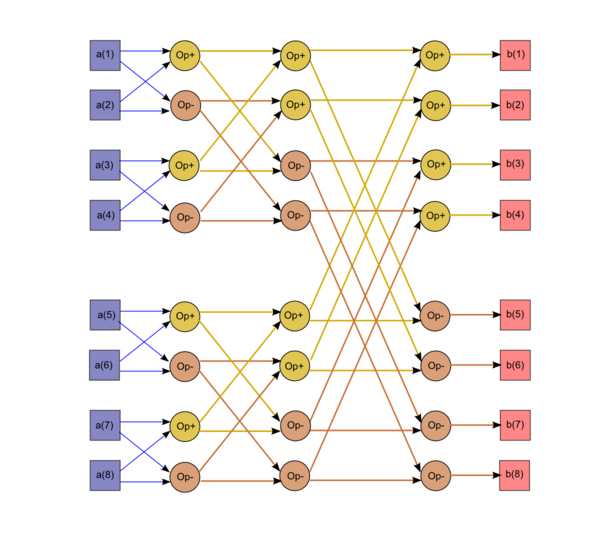
Как видно из рисунка, этот граф не является линейным ни по размерам, ни по формулам для дуг графа. По размерам он линейно-логарифмический, а формулы дуг имеют экспоненциальные компоненты.В элементарной "бабочке" на i-м шаге каждый раз участвует пара элементов массива, у которых запись их номеров, уменьшенных на единицу, в двоичной системе различается только в i-1-м бите.

1.8 Ресурс параллелизма алгоритма

Если считать только главные члены выражений, то простой алгоритм Кули-Тьюки имеет критический путь, состоящий из [math]log_{2} n [/math] операций комплексного сложения/вычитания и [math]log_{2} n [/math] операций комплексного умножения. Таким образом, простой алгоритм Кули-Тьюки может быть отнесён к логарифмическому классу по параллельной сложности. По ширине ЯПФ сложность алгоритма линейна.

1.9 Входные и выходные данные алгоритма

Входные данные: вектор [math]a[/math] (элементы [math]a_{i}[/math]).

Объём входных данных: [math]n[/math] .

Выходные данные: вектор [math]b[/math] (элементы [math]b_{i}[/math]).

Объём выходных данных: [math]n[/math].

1.10 Свойства алгоритма

Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является линейным.

При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных – логарифмическая.

При этом алгоритм полностью детерминирован.

Заметим, что простой алгоритм Кули-Тьюки не является оптимальным даже для векторов размером степень двойки. Однако здесь мы не рассматриваем другие алгоритмы БПФ.

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

В простейшем варианте алгоритм на Фортране можно записать так, что входной и выходной массивы совпадают (здесь использован массив X):

         
        subroutine STEP2(x,y,pov)
        complex x, y, pov, u, v
        u = x + y
        v = (x-y)*pov
        x = u
        y = v
        return
        end
        subroutine FFT2(X, POV, N, N2, L)
C
C L = Log2N
C N2 = N/2
C
        complex X(0:N-1), POV(0:N2-1)
        DO I = 0, L-1
            DO J = 0, N2/2**I-1
            DO K = 0, 2**I-1
                call STEP2(X(2*J*2**I+K)), X(2*J*2**I+2**I+K), POV(J*2**I-1))
            END DO
            END DO
         END DO
         return
         end

Здесь предполагается, что поворотные множители первого шага (они потом используются и на последующих шагах) предвычислены заранее и лежат в элементах массива POV (а в его нулевом элементе - единица). К сожалению, подавляющее большинство реализаций простого алгоритма Кули-Тьюки вычисляет поворотные множители одновременно с вычислением "бабочки", что её значительно замедляет.

2.2 Локальность данных и вычислений

2.2.1 Локальность реализации алгоритма

2.2.1.1 Структура обращений в память и качественная оценка локальности

Рисунок 2. Нерекурсивная реализация БПФ для степеней двойки. Общий профиль обращений в память

На рис.2 представлен профиль обращений в память для нерекурсивной реализации быстрого преобразования Фурье. Исходя из исходного кода, можно увидеть, что в программе задействовано 3 массива. Фрагменты двух из них отмечены на рис.2 зеленым, к третьему массиву относится вся остальная часть профиля.

Фрагменты 1 и 2 образованы обращениями соответственно к входному и выходному массиву. Из рисунка видно, что в обоих случаях фрагменты представляют собой аналог последовательного перебора. Анализ исходного кода показывает, что это действительно так: в обоих случаях в рамках одного цикла последовательно перебираются все элементы массива. Такие профили обладают высокой пространственной локальностью и очень низкой временной, поскольку повторные обращения просто отсутствуют.

Гораздо интереснее устроен последний фрагмент. Его можно разбить на 4 этапа, которые выделены на рис.2 оранжевым цветом. Первый этап по времени совпадает с фрагментом 1, и сам профиль также похож на последовательный перебор. Из исходного кода видно, что обращения этапа 1 – это запись в массив data либо 0, либо значений, считываемых во фрагменте 1 из массива dIn:

for( i = 0; i < nn; i++ ) {
data [ i ] = 0;
data[ i * 2 + 1 ] = dIn[ i ];
}

Видно, что обращения этапа 1 также образуют последовательный перебор. Аналогична ситуация с этапом 4, однако там на каждое 1 обращение фрагмента 1 приходится 4 последовательных обращений этапа 4.

Рассмотрим более подробно этап 2 (рис.3). Можно увидеть, что в начале этого этапа происходят обращения по всему массиву, но чем ближе к концу этапа, тем ближе к концу массива происходят обращения. Видно, что часть обращений (кривая внизу рисунка) расположены близко друг к другу, а остальные обращения разбросаны достаточно далеко и образуют нечто похожее на случайный доступ.

Рисунок 3. Основной фрагмент, этап 2

Исходный код, в котором происходят обращения данного этапа, устроен следующим образом:

while( i < n ) {
if( j > i ) {
tempr = data[ i ]; data[ i ] = data[ j ]; data[ j ] = tempr;
tempr = data[ i + 1 ]; data[ i + 1 ] = data[ j + 1 ]; 
data[ j + 1 ] = tempr;
}
m = n >> 1;
while( ( m >= 2 ) && ( j > m ) ) {
j = j - m;
m = m >> 1;
}
j = j + m;
i = i + 2;
}

Можно увидеть, что действительно обращения выполняются по двум независимым индексам – на основе переменных i и j; при этом обращения на основе индекса i образуют кривую внизу рис.3, а обращения на основе индекса j – остальные, разбросанные по всему массиву обращения.

Стоит заметить, что обращения на основе индекса j не образуют случайный доступ, а подчиняются определенному закону выбора следующего элемента. Однако с точки зрения качественной оценки локальности подобные фрагменты похожи.

Таким образом, этап 2 состоит из двух фрагментов на основе двух разных индексов. Первый из них которых обладает высокой пространственной локальностью (последовательный перебор элементов) и низкой временной (к каждому элементу происходит только два обращения). Второй обладает и достаточно низкой пространственной (элементы расположены далеко друг от друга, за исключением конца этапа), и низкой временной (к каждому элементу происходит только два обращения) локальностью.

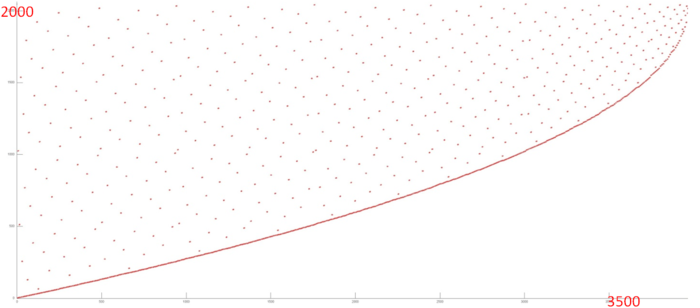
Теперь перейдем к рассмотрению самого длительного этапа 3. Отдельно данный фрагмент представлен на рис. 12.3. Исходя из рисунка, можно увидеть, что данный фрагмент состоит из нескольких итераций, причем первая итерация состоит из единичного перебора элементов массивов с некоторым шагом, вторая итерация состоит из двух проходов с одинаковым шагом (большим, чем на первой итерации), третья – из 4-х проходов и т.д., пока число проходов на итерации не начинает уменьшаться в обратную сторону. Итерации разделены на рис.4 оранжевыми линиями.

Рисунок 4. Основной фрагмент, этап 3

Видно, что внутри каждой итерации проходы обладают одинаковой структурой, а также можно предположить, что при переходе к новой итерации шаг изменяется в два раза, что и подтверждает анализ исходного кода. Также можно увидеть, что каждая итерация состоит из примерно одного числа обращений (размер выделенных оранжевыми линиями частей одинаковы).

Первая итерация похожа на последовательный перебор элементов массива, поэтому она обладает высокой пространственной и низкой временной локальностью. При увеличении шага пространственная локальность становится хуже, однако неясно, каким образом меняется временная локальность – это зависит от того, происходит ли повторный проход по тем же элементам или нет. Анализ исходного кода показывает, что каждый проход выполняется над своими элементами, поэтому временная локальность остается такой же низкой. Однако отметим, что на каждой итерации используются один и те же элементы, поэтому в целом повышает временную локальность.

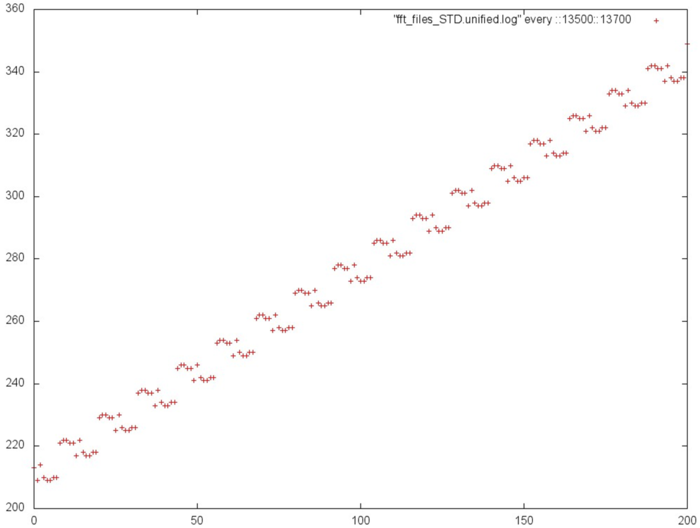
Более подробное изучение каждого прохода (рис.5, на которой приближена выделенная зеленым часть рис.4) показывает, что он обладает более сложной структурой, чем просто перебор элементов массива с некоторым шагом: в данном случае происходит серия близких друг к другу обращений, и затем сдвиг на некоторый шаг. Это приводит к некоторому улучшению как пространственной, так и временной локальности.

Рисунок 5. Основной фрагмент, небольшая часть этапа 3

2.2.1.2 Количественная оценка локальности

Основной фрагмент реализации, на основе которого были получены количественные оценки, приведен здесь (функция Kernel). Условия запуска описаны здесь.

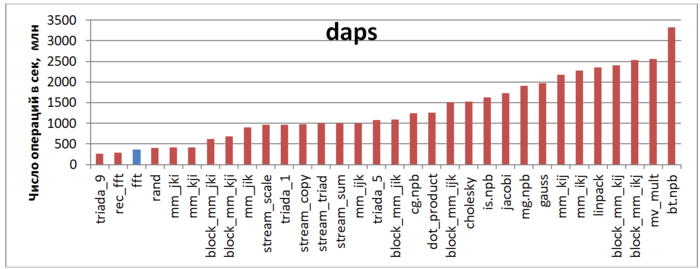
Первая оценка выполняется на основе характеристики daps, которая оценивает число выполненных обращений (чтений и записей) в память в секунду. Данная характеристика является аналогом оценки flops применительно к работе с памятью и является в большей степени оценкой производительности взаимодействия с памятью, чем оценкой локальности. Однако она служит хорошим источником информации, в том числе для сравнения с результатами по следующей характеристике cvg.

На рис.6 приведены значения daps для реализаций распространенных алгоритмов, отсортированные по возрастанию (чем больше daps, тем в общем случае выше производительность). Можно увидеть, что данная оценка показывает низкую производительность, на уровне случайного доступа в память (rand).

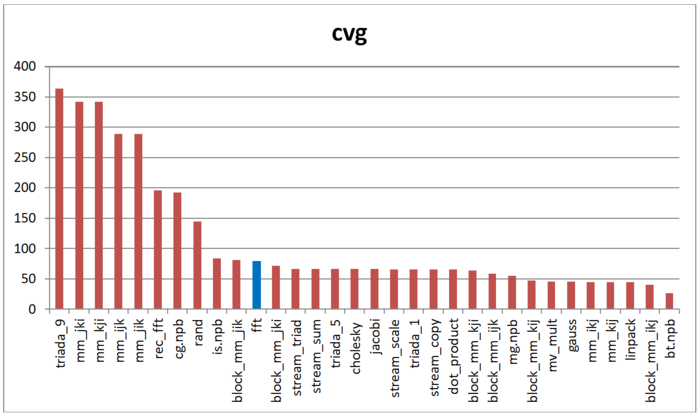
Вторая характеристика – cvg – предназначена для получения более машинно-независимой оценки локальности. Она определяет, насколько часто в программе необходимо подтягивать данные в кэш-память. Соответственно, чем меньше значение cvg, тем реже это нужно делать, тем лучше локальность

Рисунок 6. Сравнение значений оценки daps

На рис.7 приведены значения cvg для того же набора реализаций, отсортированные по убыванию (чем меньше cvg, тем в общем случае выше локальность). Можно увидеть, что, согласно данной оценке, данная реализация БПФ демонстрирует несколько лучшую локальность по сравнению со случайным доступом или рекурсивной версией, в отличие от оценки daps, результаты которой для данных программ практически совпадали. На данный момент остается неясным, чем обусловлено это различие. Однако стоит отметить, что значение локальности cvg также остается в нижней части таблицы.

Рисунок 7. Сравнение значений оценки cvg

2.4 Масштабируемость алгоритма и его реализации

2.4.2 Масштабируемость реализации алгоритма

Набор и границы значений изменяемых параметров запуска реализации алгоритма:

• число процессоров [4, 8 : 64] с шагом 8;
• размер вектора [128 : 32768] с шагом равным степени двойки.

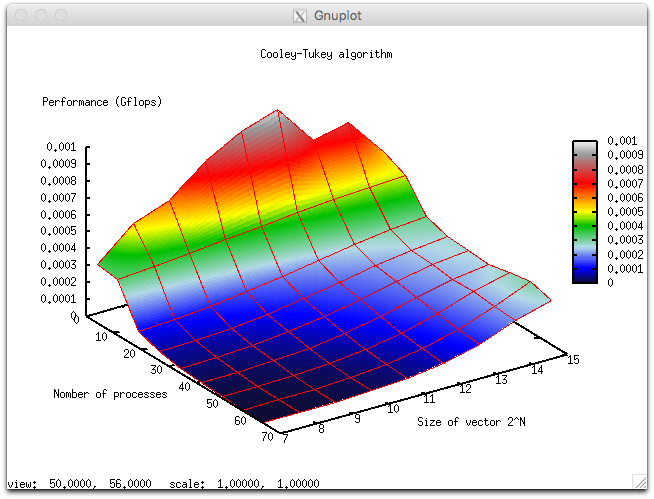
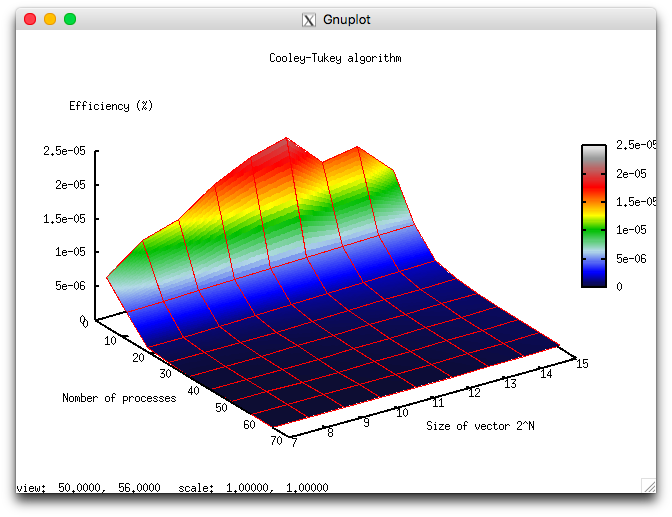
В результате проведённых экспериментов был получен следующий диапазон эффективности реализации алгоритма:

• минимальная эффективность реализации 0.000000002% (1.85994069951e-09%);
• максимальная эффективность реализации 0.00002% (2.07351573426e-05%).

На следующих рисунках приведены графики производительности и эффективности выбранной реализации алгоритма в зависимости от изменяемых параметров запуска.

Рисунок 8. Параллельная реализация алгоритма. Изменение производительности в зависимости от числа процессоров и размера области.

Рисунок 9. Параллельная реализация алгоритма. Изменение эффективности в зависимости от числа процессоров и размера матрицы.

2.6 Выводы для классов архитектур

Граф простого алгоритма Кули-Тьюки лучше всего из коммуникационных сетей отображается на сеть типа гиперкуб. Распространённость БПФ в методах решения различных задач поэтому привела к популярности идеи вычислительных систем с сетью типа гиперкуб в начале развития различных параллельных вычислительных систем. В настоящее время, однако, массово такие вычислительные системы не используются по физическим причинам, делающим гиперкуб большой размерности труднореализуемым на практике. Как видно из графа, при простом его разбиении на части прямыми, параллельными оси шагов, на первых шагах алгоритма обмены между разными частями будут отсутствовать, но, начиная с некоторого момента, они станут составлять величину, сопоставимую с количеством арифметических операций. Этого, однако, можно избежать, если примерно посередине алгоритма переупорядочить все данные. В графе это будет соответствовать смене разбиения на части. При выполнении указанных рекомендаций, алгоритм можно будет реализовать более эффективно, чем в настоящее время, и на архитектурах типа кластерной и на других архитектурах, реализующих разбиение процесса на независимые ветви.

2.7 Существующие реализации алгоритма

Простой алгоритм Кули-Тьюки быстрого преобразования Фурье для степеней двойки весьма распространён среди начинающих, использующих БПФ, и его сравнительно легко можно найти в Интернете с помощью поисковых сайтов. Как правило, эти реализации не используют описанных выше приёмов улучшения эффективности вычислений - ни для последовательной, ни для параллельной архитектуры. Связано это с тем, что сам по себе простой алгоритм Кули-Тьюки быстрого преобразования Фурье для степеней двойки проигрывает другим алгоритмам Кули-Тьюки, которые используют специфику, например, чётных степеней двойки, и потому более экономичны. Поэтому большинство исследователей, которым нужны более быстрые программы БПФ, не улучшают эффективность этого алгоритма, а меняют его на другой. Это же рекомендуем делать и читателям.