Участник:Error0x0/Алгоритм Ланцоша для арифметики с плавающей точкой с полной переортогонализацией: различия между версиями
Error0x0 (обсуждение | вклад) |
Error0x0 (обсуждение | вклад) |
||
| Строка 38: | Строка 38: | ||
== Схема реализации последовательного алгоритма == | == Схема реализации последовательного алгоритма == | ||
<syntaxhighlight lang="python"> | <syntaxhighlight lang="python"> | ||
| − | + | beta[0] = 0 # инициализация | |
| − | beta[0] = 0 | ||
q[0] = 0 | q[0] = 0 | ||
| − | for j in [1 .. k]: | + | q[1] = b / norm(b) # вычисление первого столбца |
| − | z = mul(A, q[j]) | + | for j in [1 .. k]: # k итераций |
| − | + | z = mul(A, q[j]) # вектор Ланцоша как произведение матрицы A на столбец q[j] | |
| − | for i in [1 .. j - 1]: | + | alpha[j] = scalar_mul(q[j], z) # вычисление alpha[j] |
| − | z -= mul(scalar_mul( | + | for i in [1 .. j - 1]: # полная переортогонализация |
| − | beta[j] = norm(z) | + | z -= mul(scalar_mul(z, q[i]), q[i]) |
| − | if beta[j] == 0: | + | beta[j] = norm(z) # вычисление нормы z |
| + | if beta[j] == 0: # останов, если норма z равна нулю | ||
break | break | ||
| − | result | + | result.append(next_ritz_number(alpha, beta, j)) # вычисление следующего собственного значения и вектора матрицы Tj |
return result | return result | ||
</syntaxhighlight> | </syntaxhighlight> | ||
== Последовательная сложность алгоритма == | == Последовательная сложность алгоритма == | ||
| − | + | ||
| + | Основной вклад в сложность даёт полная переортогонализация: на каждой из <math>k</math> итераций для всех <math>i \in [0...j-1]</math> выполняется <math>2n</math> умножений и <math>2n</math> сложений, итого <math>\frac{k(k-1)}{2} 4n \approx 2k^2 n</math>. | ||
| + | таким образом, для метода с полной переортогонализацией сложность составляет <math>O(k^2 n)</math>, сложность по памяти -- <math>O(kn)</math>. | ||
== Информационный граф == | == Информационный граф == | ||
| Строка 76: | Строка 78: | ||
Полная переортогонализация соответствует повторной процедуре ортогонализациии Грама-Шмидта для обеспечения ортогональности вектора <math>z</math> векторам <math>q_1, ..., q_k</math>. В случае идеально точной арифметики данная переортогонализация не требовалась бы, однако в реальных вычислениях ошибки округления приводят к потере ортогональности, в связи с чем требуется переортогонализация. | Полная переортогонализация соответствует повторной процедуре ортогонализациии Грама-Шмидта для обеспечения ортогональности вектора <math>z</math> векторам <math>q_1, ..., q_k</math>. В случае идеально точной арифметики данная переортогонализация не требовалась бы, однако в реальных вычислениях ошибки округления приводят к потере ортогональности, в связи с чем требуется переортогонализация. | ||
Однако, единственной проблемой, возникающей при отсутствии переортогонализации, является появление повторных копий чисел Ритца (собственных значений), что в случае, если не требуется установление кратностей собственных значений, допустимо. | Однако, единственной проблемой, возникающей при отсутствии переортогонализации, является появление повторных копий чисел Ритца (собственных значений), что в случае, если не требуется установление кратностей собственных значений, допустимо. | ||
| + | Вычислительная мощность алгоритма примерно равна <math>2k^2 / n</math>. | ||
Вычислительная мощность данного алгоритма: <math></math>. | Вычислительная мощность данного алгоритма: <math></math>. | ||
Версия 21:04, 1 февраля 2017
| Алгоритм Ланцоша для арифметики с плавающей точкой с полной переортогонализацией | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]O(k^2 n)[/math] |
| Объём входных данных | [math]n^2[/math] |
| Объём выходных данных | [math]n[/math] |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math]O(k \log k \log n)[/math] |
| Ширина ярусно-параллельной формы | [math]O(kn)[/math] |
Автор описания: В. А. Янушковский
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Алгоритм Ланцоша представляет собой итерационный алгоритм для вычисления собственных значений симметрической матрицы. Идея алгоритма заключается в построении матрицы [math]Q_k = [q_1, ..., q_k][/math] из ортонормированных векторов Ланцоша и использовании собственных значений трёхдиагональной матрицы [math]T_k = Q_k^T A Q_k[/math] (чисел Ритца) как приближения к искомым собственным числам матрицы[1].
1.2 Математическое описание алгоритма
Пусть дана матрица [math]A[/math]. Пусть [math]q_1 = b/||b||_2, \beta_0=0, q_0=0[/math] Алгоритм производит [math]k[/math] итераций на каждой из которых:
- вычисляется [math]z = Aq_j[/math],
- производится переортогонализация [math]z = z - \sum^{j-1}_{i=1} {(z^T q_i)q_i}[/math],
- [math]\beta_j = ||z||_2[/math], если [math]\beta_j = 0[/math], алгоритм останавливается,
- [math]q_{j+1} = z/\beta_j[/math],
- вычисляются собственные значения и векторы матрицы [math]T_j = Q_j^T A Q_j[/math].
1.3 Вычислительное ядро алгоритма
Основной вклад в сложность алгоритма даёт полная переортогонализация внутри каждой итерации:
[math]z = z - \sum^{j-1}_{i=1} {(z^T q_i)q_i}[/math]
1.4 Макроструктура алгоритма
Основные элементы алгоритма:
- Нахождение векторов Ланцоша
- Полная переортогонализация (Грамма-Шмидта)
- Вычисление собственных значений и векторов матрицы [math]T_j[/math] (числа Ритца)
1.5 Схема реализации последовательного алгоритма
beta[0] = 0 # инициализация
q[0] = 0
q[1] = b / norm(b) # вычисление первого столбца
for j in [1 .. k]: # k итераций
z = mul(A, q[j]) # вектор Ланцоша как произведение матрицы A на столбец q[j]
alpha[j] = scalar_mul(q[j], z) # вычисление alpha[j]
for i in [1 .. j - 1]: # полная переортогонализация
z -= mul(scalar_mul(z, q[i]), q[i])
beta[j] = norm(z) # вычисление нормы z
if beta[j] == 0: # останов, если норма z равна нулю
break
result.append(next_ritz_number(alpha, beta, j)) # вычисление следующего собственного значения и вектора матрицы Tj
return result
1.6 Последовательная сложность алгоритма
Основной вклад в сложность даёт полная переортогонализация: на каждой из [math]k[/math] итераций для всех [math]i \in [0...j-1][/math] выполняется [math]2n[/math] умножений и [math]2n[/math] сложений, итого [math]\frac{k(k-1)}{2} 4n \approx 2k^2 n[/math]. таким образом, для метода с полной переортогонализацией сложность составляет [math]O(k^2 n)[/math], сложность по памяти -- [math]O(kn)[/math].
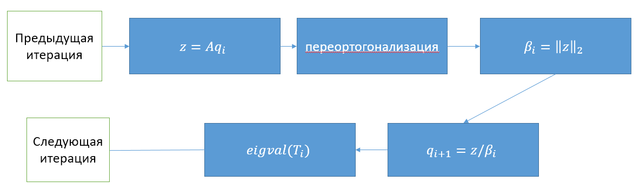
1.7 Информационный граф
1.8 Ресурс параллелизма алгоритма
Для процесса переортогонализации возможна параллельная оптимизация в двух местах:
- Итерации внутреннего цикла могут вычисляться параллельно, однако, требуется суммирование вычитаемых векторов, соответственно, сложность переортогонализации можно снизить с [math]O(kn)[/math] до [math]O(n \log k)[/math]
- В каждой итерации внутреннего цикла возможно распараллеливание вычисления выражения справа (скалярное произведение и умножение вектора на число), что теоретически позволяет снизить сложность итерации с [math]O(n)[/math] до [math]O(log(n))[/math]
1.9 Входные и выходные данные алгоритма
Входные данные: квадратная симметрическая матрица [math]A[/math] порядка [math]n[/math]
Объём входных данных: [math]n^2[/math]
Выходные данные: собственные числа матрицы
Объём выходных данных: [math]n[/math]
1.10 Свойства алгоритма
Полная переортогонализация соответствует повторной процедуре ортогонализациии Грама-Шмидта для обеспечения ортогональности вектора [math]z[/math] векторам [math]q_1, ..., q_k[/math]. В случае идеально точной арифметики данная переортогонализация не требовалась бы, однако в реальных вычислениях ошибки округления приводят к потере ортогональности, в связи с чем требуется переортогонализация. Однако, единственной проблемой, возникающей при отсутствии переортогонализации, является появление повторных копий чисел Ритца (собственных значений), что в случае, если не требуется установление кратностей собственных значений, допустимо. Вычислительная мощность алгоритма примерно равна [math]2k^2 / n[/math].
Вычислительная мощность данного алгоритма: [math][/math].
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Библиотека NAG Library содержит ряд процедур для решения СЛАУ и поиска собственных значений на основе алгоритма Ланцоша.
MATLAB и GNU Octave позволяют с помощью функции eigs() находить собственные значения на основе данного алгоритма.
Matlab-реализация доступна как часть Gaussian Belief Propagation Matlab Package. GraphLab содержит несколько параллельных реализаций алгоритма на C++.
3 Литература
- ↑ Деммель Дж. Вычислительная линейная алгебра