Участник:Galkina/Метод Якоби вычисления собственных значений симметричной матрицы: различия между версиями
Игорь (обсуждение | вклад) |
Frolov (обсуждение | вклад) |
||
| (не показаны 103 промежуточные версии 4 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | {{Assignment|ASA|Frolov}} | |
| + | |||
| + | {{algorithm | ||
| + | | name = Метод Якоби вычисления собственных значений симметричной матрицы | ||
| + | | serial_complexity = <math>O(n^3)</math> | ||
| + | | pf_height = <math>O(n^2)</math> | ||
| + | | pf_width = <math>O(n)</math> | ||
| + | | input_data = <math>\frac{n (n + 1)}{2}</math> | ||
| + | | output_data = <math>n</math> | ||
| + | }} | ||
| + | |||
| + | Авторы описания: [[Участник: Galkina|А.С.Галкина]] (входные и выходные данные, математическое описание алгоритма и др.), [[Участник: Игорь|И.А.Плахов]] (ресурс параллелизма алгоритма,последовательная сложность алгоритма и др.) Вклад авторов считать равноценным. | ||
== Свойства и структура алгоритма == | == Свойства и структура алгоритма == | ||
| Строка 5: | Строка 16: | ||
=== Общее описание алгоритма === | === Общее описание алгоритма === | ||
| − | Метод Якоби — итерационный алгоритм для вычисления собственных значений и собственных векторов вещественной симметричной матрицы. Карл Густав Якоб Якоби, в честь которого назван этот метод, предложил его в 1846 году, хотя использоваться он начал только в 1950-х годах с появлением компьютеров. Суть алгоритма заключается в том, чтобы по заданной симметрической матрице <math>A = A_0</math> построить последовательность ортогонально подобных матриц <math>A_1,A_2, | + | Метод Якоби — итерационный алгоритм для вычисления собственных значений и собственных векторов вещественной симметричной матрицы. Карл Густав Якоб Якоби, в честь которого назван этот метод, предложил его в 1846 году, хотя использоваться он начал только в 1950-х годах с появлением компьютеров. |
| + | Суть алгоритма заключается в том, чтобы по заданной симметрической матрице <math>A = A_0</math> построить последовательность ортогонально подобных матриц <math>A_1,A_2,\dotsc,A_m</math>, сходящуюся к диагональной матрице, на диагонали которой стоят собственные значения. Для построения этой последовательности применяется специально подобранная матрица поворота <math>J_i</math>, такая что норма наддиагональной части <math>of\!f(A)=\sqrt{\sum\limits_{1 \le j < k \le n} a_{jk}^2}</math> уменьшается при каждом повороте матрицы <math>A</math>. Вычисление останавливается, когда угол поворота становится близок к нулю, либо когда максимальный внедиагональный элемент становится меньше заранее выбранного порогового значения. | ||
=== Математическое описание алгоритма === | === Математическое описание алгоритма === | ||
| Строка 15: | Строка 27: | ||
При подходящем выборе <math>J_i</math> матрица <math>A_m</math> для больших m будет близка к диагональной матрице <math>\Lambda</math>. | При подходящем выборе <math>J_i</math> матрица <math>A_m</math> для больших m будет близка к диагональной матрице <math>\Lambda</math>. | ||
| − | Матрица <math>J_i</math> выбирается так, чтобы сделать нулями пару внедиагональных элементов матрицы <math>A_{i+1}</math>. | + | Матрица <math>J_i</math> выбирается так, чтобы сделать нулями пару внедиагональных элементов матрицы <math>A_{i+1}</math> <ref name="VVVVVV">Деммель Дж. Вычислительная линейная алгебра. - М.: МИР, 2001 - С. 244-248</ref>. |
<!-- полноценный TEX, похоже, не поддерживается =( --> | <!-- полноценный TEX, похоже, не поддерживается =( --> | ||
| + | |||
| + | | ||
| + | <math>j</math> | ||
| + | | ||
| + | <math>k</math> | ||
| + | |||
<math> | <math> | ||
J_i = | J_i = | ||
| Строка 27: | Строка 45: | ||
\\ | \\ | ||
k \\ | k \\ | ||
| − | |||
\\ | \\ | ||
\\ | \\ | ||
| Строка 35: | Строка 52: | ||
<math> | <math> | ||
\begin{bmatrix} | \begin{bmatrix} | ||
| − | & 1 & & & & & | + | & 1 & & & & & & & & \\ |
| − | & & 1 & & & & | + | & & 1 & & & & & & & \\ |
| − | & & & \ddots & & & | + | & & & \ddots & & & & & & \\ |
| − | & & & & \cos(\theta) & & \sin(\theta) & & & \\ | + | & & & & \cos(\theta) & & -\sin(\theta) & & & \\ |
| − | & & & & & \ddots & | + | & & & & & \ddots & & & & \\ |
| − | & & & & \sin(\theta) & & \cos(\theta) & & & \\ | + | & & & & \sin(\theta) & & \cos(\theta) & & & \\ |
| − | & & & & & & | + | & & & & & & & \ddots & & \\ |
| − | & & & & & & | + | & & & & & & & & 1 & \\ |
| − | & & & & & & | + | & & & & & & & & & 1 \\ |
\end{bmatrix} | \end{bmatrix} | ||
</math> | </math> | ||
| Строка 58: | Строка 75: | ||
\end{align}</math> | \end{align}</math> | ||
| − | Можно выбрать <math>\theta</math> так, чтобы <math>a_{jk}^{(i+1)} = 0</math> и <math>a_{kj}^{(i+1)} = 0</math>. | + | Можно выбрать <math>\theta</math> так, чтобы <math>a_{jk}^{(i+1)} = 0</math> и <math>a_{kj}^{(i+1)} = 0</math>. Отсюда получим равенство |
| + | |||
| + | : <math> \frac{a_{jj}^{(i)} - a_{kk}^{(i)}}{2 a_{jk}^{(i)}} = \frac{c^2 - s^2}{2sc} = \frac{\cos (2\theta)}{\sin (2\theta)} = \operatorname{ctg}(2\theta) \equiv \tau </math>. | ||
| − | + | Если <math> a_{jj}^{(i)} = a_{kk}^{(i)}</math>, то <math>\theta = \frac{\pi}{4}</math>. | |
| − | |||
| − | |||
| − | |||
| − | = | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | \ | ||
| − | |||
| − | |||
| − | |||
| − | + | Положим <math>t = \frac{s}{c} = \operatorname{tg}(\theta)</math> и заметим, что <math>t^2 - 2t\tau + 1 = 0</math>. Решая квадратное уравнение, находим <math>t = \frac{\operatorname{sign}(\tau)}{|\tau| + \sqrt{1+\tau^2}}, c = \frac{1}{\sqrt{1+t^2}}, s = tc</math>. | |
| − | + | Выбор параметров <math>j</math> и <math>k</math> производится путем построчного циклического обхода внедиагональных элементов матрицы <math>A</math>. | |
| − | |||
| − | |||
| − | |||
| − | + | === Вычислительное ядро алгоритма === | |
| + | Рассматривая отдельную итерацию, можно считать, что вычислительное ядро составляют множественные вычисления элементов матрицы <math>a_{jm}^{(i+1)} = a_{mj}^{(i+1)}</math> и <math>a_{km}^{(i+1)} = a_{mk}^{(i+1)}</math>, <math>m \ne j,k</math> в процессе применения матрицы поворота <math>J_i</math> к матрице <math>A</math>: | ||
| + | : <math>\begin{align} | ||
| + | a_{jm}^{(i+1)} &= a_{mj}^{(i+1)} = c \, a_{jm}^{(i)} - s \, a_{km}^{(i)} & m \ne j,k \\ | ||
| + | a_{km}^{(i+1)} &= a_{mk}^{(i+1)} = s \, a_{jm}^{(i)} + c \, a_{km}^{(i)} & m \ne j,k, | ||
| + | \end{align}</math> | ||
| − | + | каждое из которых повторяется по <math> (n-2) </math> раза, а также вычисление элементов <math>a_{jj}^{(i+1)} </math> и <math>a_{kk}^{(i+1)} </math>: | |
| − | + | : <math>\begin{align} | |
| − | + | a_{jj}^{(i+1)} &= c^2\, a_{jj}^{(i)} - 2\, s c \,a_{jk}^{(i)} + s^2\, a_{kk}^{(i)} \\ | |
| − | + | a_{kk}^{(i+1)} &= s^2 \,a_{jj}^{(i)} + 2 s c\, a_{jk}^{(i)} + c^2 \, a_{kk}^{(i)} | |
| − | + | \end{align}</math> | |
| − | + | ||
| − | \begin{ | + | === Макроструктура алгоритма === |
| − | + | Основную часть метода составляет процедура применения вращения к матрице <math>A</math>, которая в дальнейшем будет обозначена как '''''Jakobi-Rotation<math>(A,j,k)</math>'''''. | |
| − | |||
| − | \end{ | ||
| − | </math> | ||
| − | + | Эту процедуру, в свою очередь, можно разделить на две логические части: | |
| + | # Определение угла поворота <math>\theta</math> по элементам матрицы <math>a_{jj}</math>, <math>a_{kk}</math> и <math>a_{jk}</math>; | ||
| + | # Поворот матрицы <math>A</math> (изменяются лишь строки и столбцы, соответствующие индексам <math>j</math> и <math>k</math>). | ||
| − | + | === Схема реализации последовательного алгоритма === | |
| + | Алгоритм можно описать следующим образом <ref name="VVVVVV" />: | ||
| − | + | 1. Выбрать пару индексов j,k | |
| + | 2. Обратиться к процедуре '''''Jakobi-Rotation<math>(A,j,k)</math>''''' | ||
| + | Если <math>A</math> не достаточно близка к диагональной матрице, перейти к шагу 1. | ||
| − | + | Существует несколько способов выбора пары <math>j,k</math>. Наиболее простой и быстрый способ — построчный циклический обход внедиагональных элементов матрицы <math>A</math>: | |
| − | == | + | repeat |
| + | for <math>j=1</math> to <math>n-1</math> | ||
| + | for <math>k=j+1</math> to <math>n</math> | ||
| + | выполнить процедуру '''''Jakobi-Rotation<math>(A,j,k)</math>''''' | ||
| + | end for | ||
| + | end for | ||
| + | пока <math>A</math> не достаточно близка к диагональной матрице | ||
| − | === | + | Процедура '''''Jakobi-Rotation<math>(A,j,k)</math>''''' — это следующий алгоритм: |
| + | Если <math>|a_{jk}|</math> достаточно мал, вычисление заканчивается. В противном случае выполняются следующие действия: | ||
| + | 1. Если <math>a_{jj}==a_{kk}</math>, то угол <math>\theta=\frac{\pi}{4}</math>. | ||
| + | В остальных случаях находим параметры <math>\tau,\ t,\ c,\ s</math>: | ||
| + | <math>\begin{align} | ||
| + | \tau &= \frac{a_{jj}-a_{kk}}{2\,a_{jk}} \\ | ||
| + | t &= \frac{sign(\tau)}{|\tau|+\sqrt{1+\tau^2}} \\ | ||
| + | c &= \frac{1}{\sqrt{1+t^2}} \\ | ||
| + | s &= c\,t | ||
| + | \end{align}</math> | ||
| + | 2. Выполняется поворот матрицы (изменяются лишь строки и столбцы, соответствующие индексам <math>i</math> и <math>j</math>): | ||
| + | <math>A = R^T(j,k,\theta)\cdot A\cdot R(j,k,\theta), \qquad J_i = R(j,k,\theta),\ c = \cos \theta,\ s = \sin \theta </math> | ||
=== Последовательная сложность алгоритма === | === Последовательная сложность алгоритма === | ||
| + | |||
| + | Для осуществления одной итерации метода Якоби для матрицы размера <math>(n\times n)</math> требуется выполнить: | ||
| + | |||
| + | Для вычислительного ядра — | ||
| + | * <math> 4n+4 </math> умножений, | ||
| + | * <math> 2n+2 </math> сложений. | ||
| + | |||
| + | Для остальной части алгоритма — | ||
| + | * <math> 3 </math> умножения, | ||
| + | * <math> 3 </math> деления, | ||
| + | * <math> 5 </math> сложений (вычитаний), | ||
| + | * <math> 2 </math> извлечения квадратного корня. | ||
| + | |||
| + | Умножения и сложения (вычитания) составляют основную часть алгоритма. | ||
| + | |||
| + | Так как выбор индексов <math>j</math> и <math>k</math> осуществляется путем перебора внедиагональных элементов матрицы, для полного прохода потребуется <math>\frac{n(n-1)}{2}</math> итераций. | ||
| + | |||
| + | Таким образом, при классификации по последовательной сложности метод Якоби вычисления собственных значений симметричной матрицы относится к алгоритмам с кубической сложностью. | ||
=== Информационный граф === | === Информационный граф === | ||
| + | |||
| + | Граф алгоритма состоит из трёх групп вершин. | ||
| + | |||
| + | '''Первой''' группе вершин (J) соответствует вычисление значений c и s. | ||
| + | |||
| + | '''Второй''' группе вершин (А) соответствует вычисление значений элементов <math>a_{jm}^{(i+1)} = a_{mj}^{(i+1)}</math> и <math>a_{km}^{(i+1)} = a_{mk}^{(i+1)}</math>, <math>m \ne j,k</math>. | ||
| + | |||
| + | '''Третьей''' группе вершин (B) соответствует вычисление значений элементов <math>a_{jj}^{(i+1)} </math> и <math>a_{kk}^{(i+1)} </math>. | ||
| + | |||
| + | <!-- | ||
| + | <center> | ||
| + | <div class="thumb"> | ||
| + | <div class="thumbinner" style="width:{{#expr: 3 * (400 + 35) + 4 * (3 - 1) + 8}}px"> | ||
| + | <gallery widths=400px heights=400px> | ||
| + | File:Информационный_граф_метода_якоби.png|Рисунок 1. Граф одной итерации алгоритма без отображения входных и выходных данных. | ||
| + | File:ГрафJ.png|Рисунок 2. Внутренний граф вершин J с входными параметрами <math>x = a_{jj}^{(i)}, y = a_{kk}^{(i)}, z = a_{jk}^{(i)}</math>. | ||
| + | </gallery> | ||
| + | </div> | ||
| + | </div> | ||
| + | </center> | ||
| + | --> | ||
| + | |||
| + | [[File:Информационный_граф_метода_якоби.png|none|thumb|2000px|Рисунок 1. Граф одной итерации алгоритма без отображения входных и выходных данных.]] | ||
| + | |||
| + | [[File:ГрафJ.png|none|thumb|2000px|Рисунок 2. Внутренний граф вершин J с входными параметрами <math>x = a_{jj}^{(i)}, y = a_{kk}^{(i)}, z = a_{jk}^{(i)}</math>.]] | ||
=== Ресурс параллелизма алгоритма === | === Ресурс параллелизма алгоритма === | ||
| + | |||
| + | Для выполнения одной итерации требуется последовательно выполнить следующие действия: | ||
| + | # вычислить <math>\tau</math> (2 операции сложения, 1 операция деления) | ||
| + | # вычислить <math>t</math> (1 операция сравнения, 1 операция взятия модуля, 2 операции сложения, 1 операция умножения, 1 операция деления, 1 операция извлечения квадратного корня) | ||
| + | # вычислить <math>c</math> (1 операция сложения, 1 операция умножения, 1 операция деления, 1 операция извлечения квадратного корня) и <math>s</math> (1 операция умножения) | ||
| + | |||
| + | После этого выполняется ярус, отвечающий за применение поворота к матрице <math>A</math> с параллельным выполнением <math>2(n-2)</math> операций вычисления элементов матрицы <math>a_{jm}^{(i+1)} = a_{mj}^{(i+1)}</math> и <math>a_{km}^{(i+1)} = a_{mk}^{(i+1)}</math>, <math>m \ne j,k</math> , а также 2 операций вычисления элементов <math>a_{jj}^{(i+1)} </math> и <math>a_{kk}^{(i+1)} </math>. Наибольшее количество операций содержится в вычислении последних двух элементов (по 6 умножений и 3 сложения). | ||
| + | |||
| + | Суммарное количество итераций зависит от входных данных и заданного значения погрешности. Один "цикл" (полный проход по внедиагональным элементам) осуществляется за <math>N = \frac{n(n-1)}{2}</math> итераций. Асимптотически метод сходится квадратично <ref>Wilkinson J. H. The Algebraic Eigenvalue Problem // Oxford University Press, UK, 1965, P. 270</ref>. Как правило, для сходимости метода Якоби требуется от 5 до 10 циклов, что хуже, чем у конкурирующих алгоритмов <ref name="VVVVVV" />. | ||
| + | |||
| + | Таким образом, при классификации по высоте ЯПФ метод Якоби относится к алгоритмам со сложностью <math>O(n^2)</math> , а при классификации по ширине ЯПФ — к алгоритмам со сложностью <math>O(n)</math>. | ||
=== Входные и выходные данные алгоритма === | === Входные и выходные данные алгоритма === | ||
| Строка 130: | Строка 203: | ||
'''Объём входных данных''': <math>\frac{n (n + 1)}{2}</math> (в силу симметричности достаточно хранить только диагональ и над/поддиагональные элементы). В разных реализациях эта экономия хранения может быть выполнена разным образом. | '''Объём входных данных''': <math>\frac{n (n + 1)}{2}</math> (в силу симметричности достаточно хранить только диагональ и над/поддиагональные элементы). В разных реализациях эта экономия хранения может быть выполнена разным образом. | ||
| − | '''Выходные данные''': | + | '''Выходные данные''': вектор собственных значений <math>\Lambda</math> (элементы <math>\lambda_{ii}</math>). |
| − | '''Объём выходных данных''': <math> n </math> | + | '''Объём выходных данных''': <math> n </math>. |
=== Свойства алгоритма === | === Свойства алгоритма === | ||
| + | |||
| + | Метод Якоби является самым медленным из имеющихся алгоритмов вычисления собственных значений симметричной матрицы. Тем не менее, он способен вычислять малые собственные числа и отвечающие им собственные векторы с гораздо большей точностью, чем другие методы <ref name="VVVVVV" />. Кроме того, он не предполагает первоначального приведения матрицы к трехдиагональной форме. | ||
| + | |||
| + | Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов для метода Якоби является линейным. | ||
| + | |||
| + | Вычислительная мощность алгоритма линейна. | ||
| + | |||
| + | Метод Якоби не детерминирован, так как является итерационным алгоритмом с выходом по точности: число итераций зависит от входных данных и порогового значения. | ||
| + | |||
| + | Дуги информационного графа, исходящие из вершин, соответствующих вычислениям значений <math>c</math> и <math>s</math>, образуют пучки рассылок линейной мощности. | ||
== Программная реализация алгоритма == | == Программная реализация алгоритма == | ||
| + | |||
| + | === Особенности реализации последовательного алгоритма === | ||
| + | |||
| + | === Локальность данных и вычислений === | ||
| + | |||
| + | === Возможные способы и особенности параллельной реализации алгоритма === | ||
=== Масштабируемость алгоритма и его реализации === | === Масштабируемость алгоритма и его реализации === | ||
| + | Исследование масштабируемости проводилось на суперкомпьютере "Ломоносов" [http://parallel.ru/cluster Суперкомпьютерного комплекса Московского Государственного Университета имени М.В. Ломоносова]. Алгоритм реализован на языке C++ с использованием средств MPI. Компиляция производилась с помощью команды mpicxx с использованием компилятора Intel с OpenMPI и библиотеки MKL. Были подключены следующие модули: openmpi/1.5.5-icc, intel/13.1.0, mkl/4.0.2.146. Программа была запущена в очередях test и regular4. | ||
| + | |||
| + | Значения изменяемых параметров запуска реализации алгоритма: | ||
| + | * число процессов: 2, 4, 8, 16, 32, 64; | ||
| + | * число элементов в матрице: 900, 3600, 8100, 14400, 22500, 32400, 44100, 57600, 72900, 90000. | ||
| + | |||
| + | На следующих рисунках приведены графики времени выполнения и производительности выбранной реализации алгоритма в зависимости от изменяемых параметров запуска | ||
| + | |||
| + | [[File:jacobi_time.jpg|thumb|center|1500px|Рисунок 3. Изменение времени выполнения в зависимости от числа процессов и размера входной матрицы]] | ||
| + | [[File:jacobi_perform.jpg|thumb|center|1500px|Рисунок 4. Изменение производительности в зависимости от числа процессов и размера входной матрицы]] | ||
| + | |||
| + | На Рис.4 видно, что при увеличении количества процессов производительность сначала увеличивается, а затем уменьшается. Время работы алгоритма резко увеличивается при увеличении размеров матрицы, что обусловлено большим количеством сообщений, обрабатываемых корневым процессом. Полученные результаты говорят о плохой масштабируемости алгоритма. | ||
| + | |||
| + | Реализация алгоритма доступна по [http://pastebin.com/juwPJRhH ссылке]. | ||
| + | |||
| + | === Динамические характеристики и эффективность реализации алгоритма === | ||
| + | |||
| + | === Выводы для классов архитектур === | ||
=== Существующие реализации алгоритма === | === Существующие реализации алгоритма === | ||
| + | |||
| + | Существует библиотека JACOBI_EIGENVALUE, реализующая последовательный вариант метода Якоби на языках программирования [http://people.sc.fsu.edu/~jburkardt/c_src/jacobi_eigenvalue/jacobi_eigenvalue.html С], [http://people.sc.fsu.edu/~jburkardt/cpp_src/jacobi_eigenvalue/jacobi_eigenvalue.html С++], [http://people.sc.fsu.edu/~jburkardt/f77_src/jacobi_eigenvalue/jacobi_eigenvalue.html FORTRAN77], [http://people.sc.fsu.edu/~jburkardt/f_src/jacobi_eigenvalue/jacobi_eigenvalue.html FORTRAN90], [http://people.sc.fsu.edu/~jburkardt/m_src/jacobi_eigenvalue/jacobi_eigenvalue.html MATLAB], [http://people.sc.fsu.edu/~jburkardt/py_src/jacobi_eigenvalue/jacobi_eigenvalue.html Python]. | ||
| + | Данная библиотека распространяется по лицензии [http://people.sc.fsu.edu/~jburkardt/txt/gnu_lgpl.txt GNU LESSER GENERAL PUBLIC LICENSE]. | ||
| + | |||
| + | Существует также параллельная [http://ieeexplore.ieee.org/document/6310877/ реализация] метода на платформе CUDA. | ||
== Литература == | == Литература == | ||
| + | |||
| + | <references \> | ||
Текущая версия на 15:43, 16 декабря 2016
 | Эта работа успешно выполнена Преподавателю: в основное пространство, в подстраницу Данное задание было проверено и зачтено. Проверено Frolov и ASA. |
| Метод Якоби вычисления собственных значений симметричной матрицы | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]O(n^3)[/math] |
| Объём входных данных | [math]\frac{n (n + 1)}{2}[/math] |
| Объём выходных данных | [math]n[/math] |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math]O(n^2)[/math] |
| Ширина ярусно-параллельной формы | [math]O(n)[/math] |
Авторы описания: А.С.Галкина (входные и выходные данные, математическое описание алгоритма и др.), И.А.Плахов (ресурс параллелизма алгоритма,последовательная сложность алгоритма и др.) Вклад авторов считать равноценным.
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Метод Якоби — итерационный алгоритм для вычисления собственных значений и собственных векторов вещественной симметричной матрицы. Карл Густав Якоб Якоби, в честь которого назван этот метод, предложил его в 1846 году, хотя использоваться он начал только в 1950-х годах с появлением компьютеров. Суть алгоритма заключается в том, чтобы по заданной симметрической матрице [math]A = A_0[/math] построить последовательность ортогонально подобных матриц [math]A_1,A_2,\dotsc,A_m[/math], сходящуюся к диагональной матрице, на диагонали которой стоят собственные значения. Для построения этой последовательности применяется специально подобранная матрица поворота [math]J_i[/math], такая что норма наддиагональной части [math]of\!f(A)=\sqrt{\sum\limits_{1 \le j \lt k \le n} a_{jk}^2}[/math] уменьшается при каждом повороте матрицы [math]A[/math]. Вычисление останавливается, когда угол поворота становится близок к нулю, либо когда максимальный внедиагональный элемент становится меньше заранее выбранного порогового значения.
1.2 Математическое описание алгоритма
Исходные данные: симметрическая матрица [math]A[/math] (элементы [math]a_{ij}[/math]).
Вычисляемые данные: диагональная матрица [math]\Lambda[/math] (элементы [math]\lambda_{ij}[/math]).
Матрица [math]A_{i+1}[/math] получается из [math]A_i[/math] по формуле [math]A_{i+1}={J_i}^TA_iJ_i[/math], где [math]J_i[/math] — ортогональная матрица, называемая вращением Якоби. При подходящем выборе [math]J_i[/math] матрица [math]A_m[/math] для больших m будет близка к диагональной матрице [math]\Lambda[/math].
Матрица [math]J_i[/math] выбирается так, чтобы сделать нулями пару внедиагональных элементов матрицы [math]A_{i+1}[/math] [1].
[math]j[/math]
[math]k[/math]
[math] J_i = \begin{matrix} \\ \\ \\ j \\ \\ k \\ \\ \\ \\ \end{matrix} [/math] [math] \begin{bmatrix} & 1 & & & & & & & & \\ & & 1 & & & & & & & \\ & & & \ddots & & & & & & \\ & & & & \cos(\theta) & & -\sin(\theta) & & & \\ & & & & & \ddots & & & & \\ & & & & \sin(\theta) & & \cos(\theta) & & & \\ & & & & & & & \ddots & & \\ & & & & & & & & 1 & \\ & & & & & & & & & 1 \\ \end{bmatrix} [/math]
Обозначим [math]s = \sin \theta[/math] и [math]c = \cos \theta[/math]. Тогда матрица [math]A_{i+1}[/math] состоит из следующих элементов:
- [math]\begin{align} a_{jj}^{(i+1)} &= c^2\, a_{jj}^{(i)} - 2\, s c \,a_{jk}^{(i)} + s^2\, a_{kk}^{(i)} \\ a_{kk}^{(i+1)} &= s^2 \,a_{jj}^{(i)} + 2 s c\, a_{jk}^{(i)} + c^2 \, a_{kk}^{(i)} \\ a_{jk}^{(i+1)} &= a_{kj}^{(i+1)} = (c^2 - s^2 ) \, a_{jk}^{(i)} + s c \, (a_{kk}^{(i)} - a_{jj}^{(i)} ) \\ a_{jm}^{(i+1)} &= a_{mj}^{(i+1)} = c \, a_{jm}^{(i)} - s \, a_{km}^{(i)} & m \ne j,k \\ a_{km}^{(i+1)} &= a_{mk}^{(i+1)} = s \, a_{jm}^{(i)} + c \, a_{km}^{(i)} & m \ne j,k \\ a_{ml}^{(i+1)} &= a_{ml}^{(i)} &m,l \ne j,k \end{align}[/math]
Можно выбрать [math]\theta[/math] так, чтобы [math]a_{jk}^{(i+1)} = 0[/math] и [math]a_{kj}^{(i+1)} = 0[/math]. Отсюда получим равенство
- [math] \frac{a_{jj}^{(i)} - a_{kk}^{(i)}}{2 a_{jk}^{(i)}} = \frac{c^2 - s^2}{2sc} = \frac{\cos (2\theta)}{\sin (2\theta)} = \operatorname{ctg}(2\theta) \equiv \tau [/math].
Если [math] a_{jj}^{(i)} = a_{kk}^{(i)}[/math], то [math]\theta = \frac{\pi}{4}[/math].
Положим [math]t = \frac{s}{c} = \operatorname{tg}(\theta)[/math] и заметим, что [math]t^2 - 2t\tau + 1 = 0[/math]. Решая квадратное уравнение, находим [math]t = \frac{\operatorname{sign}(\tau)}{|\tau| + \sqrt{1+\tau^2}}, c = \frac{1}{\sqrt{1+t^2}}, s = tc[/math].
Выбор параметров [math]j[/math] и [math]k[/math] производится путем построчного циклического обхода внедиагональных элементов матрицы [math]A[/math].
1.3 Вычислительное ядро алгоритма
Рассматривая отдельную итерацию, можно считать, что вычислительное ядро составляют множественные вычисления элементов матрицы [math]a_{jm}^{(i+1)} = a_{mj}^{(i+1)}[/math] и [math]a_{km}^{(i+1)} = a_{mk}^{(i+1)}[/math], [math]m \ne j,k[/math] в процессе применения матрицы поворота [math]J_i[/math] к матрице [math]A[/math]:
- [math]\begin{align} a_{jm}^{(i+1)} &= a_{mj}^{(i+1)} = c \, a_{jm}^{(i)} - s \, a_{km}^{(i)} & m \ne j,k \\ a_{km}^{(i+1)} &= a_{mk}^{(i+1)} = s \, a_{jm}^{(i)} + c \, a_{km}^{(i)} & m \ne j,k, \end{align}[/math]
каждое из которых повторяется по [math] (n-2) [/math] раза, а также вычисление элементов [math]a_{jj}^{(i+1)} [/math] и [math]a_{kk}^{(i+1)} [/math]:
- [math]\begin{align} a_{jj}^{(i+1)} &= c^2\, a_{jj}^{(i)} - 2\, s c \,a_{jk}^{(i)} + s^2\, a_{kk}^{(i)} \\ a_{kk}^{(i+1)} &= s^2 \,a_{jj}^{(i)} + 2 s c\, a_{jk}^{(i)} + c^2 \, a_{kk}^{(i)} \end{align}[/math]
1.4 Макроструктура алгоритма
Основную часть метода составляет процедура применения вращения к матрице [math]A[/math], которая в дальнейшем будет обозначена как Jakobi-Rotation[math](A,j,k)[/math].
Эту процедуру, в свою очередь, можно разделить на две логические части:
- Определение угла поворота [math]\theta[/math] по элементам матрицы [math]a_{jj}[/math], [math]a_{kk}[/math] и [math]a_{jk}[/math];
- Поворот матрицы [math]A[/math] (изменяются лишь строки и столбцы, соответствующие индексам [math]j[/math] и [math]k[/math]).
1.5 Схема реализации последовательного алгоритма
Алгоритм можно описать следующим образом [1]:
1. Выбрать пару индексов j,k 2. Обратиться к процедуре Jakobi-Rotation[math](A,j,k)[/math] Если [math]A[/math] не достаточно близка к диагональной матрице, перейти к шагу 1.
Существует несколько способов выбора пары [math]j,k[/math]. Наиболее простой и быстрый способ — построчный циклический обход внедиагональных элементов матрицы [math]A[/math]:
repeat
for [math]j=1[/math] to [math]n-1[/math]
for [math]k=j+1[/math] to [math]n[/math]
выполнить процедуру Jakobi-Rotation[math](A,j,k)[/math]
end for
end for
пока [math]A[/math] не достаточно близка к диагональной матрице
Процедура Jakobi-Rotation[math](A,j,k)[/math] — это следующий алгоритм:
Если [math]|a_{jk}|[/math] достаточно мал, вычисление заканчивается. В противном случае выполняются следующие действия: 1. Если [math]a_{jj}==a_{kk}[/math], то угол [math]\theta=\frac{\pi}{4}[/math]. В остальных случаях находим параметры [math]\tau,\ t,\ c,\ s[/math]: [math]\begin{align} \tau &= \frac{a_{jj}-a_{kk}}{2\,a_{jk}} \\ t &= \frac{sign(\tau)}{|\tau|+\sqrt{1+\tau^2}} \\ c &= \frac{1}{\sqrt{1+t^2}} \\ s &= c\,t \end{align}[/math] 2. Выполняется поворот матрицы (изменяются лишь строки и столбцы, соответствующие индексам [math]i[/math] и [math]j[/math]): [math]A = R^T(j,k,\theta)\cdot A\cdot R(j,k,\theta), \qquad J_i = R(j,k,\theta),\ c = \cos \theta,\ s = \sin \theta [/math]
1.6 Последовательная сложность алгоритма
Для осуществления одной итерации метода Якоби для матрицы размера [math](n\times n)[/math] требуется выполнить:
Для вычислительного ядра —
- [math] 4n+4 [/math] умножений,
- [math] 2n+2 [/math] сложений.
Для остальной части алгоритма —
- [math] 3 [/math] умножения,
- [math] 3 [/math] деления,
- [math] 5 [/math] сложений (вычитаний),
- [math] 2 [/math] извлечения квадратного корня.
Умножения и сложения (вычитания) составляют основную часть алгоритма.
Так как выбор индексов [math]j[/math] и [math]k[/math] осуществляется путем перебора внедиагональных элементов матрицы, для полного прохода потребуется [math]\frac{n(n-1)}{2}[/math] итераций.
Таким образом, при классификации по последовательной сложности метод Якоби вычисления собственных значений симметричной матрицы относится к алгоритмам с кубической сложностью.
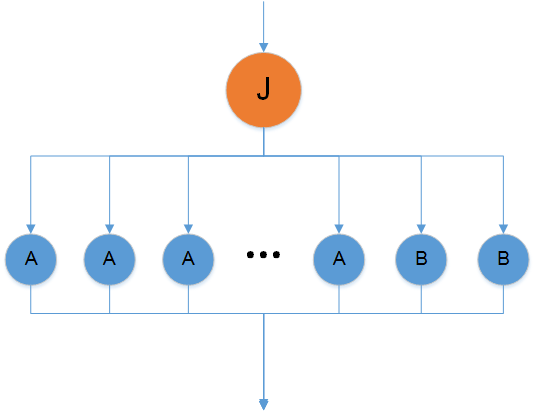
1.7 Информационный граф
Граф алгоритма состоит из трёх групп вершин.
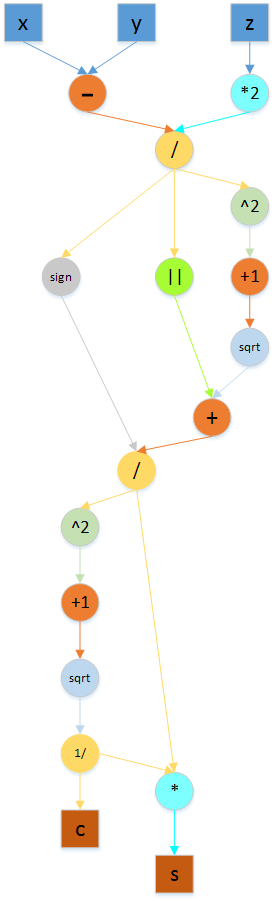
Первой группе вершин (J) соответствует вычисление значений c и s.
Второй группе вершин (А) соответствует вычисление значений элементов [math]a_{jm}^{(i+1)} = a_{mj}^{(i+1)}[/math] и [math]a_{km}^{(i+1)} = a_{mk}^{(i+1)}[/math], [math]m \ne j,k[/math].
Третьей группе вершин (B) соответствует вычисление значений элементов [math]a_{jj}^{(i+1)} [/math] и [math]a_{kk}^{(i+1)} [/math].
1.8 Ресурс параллелизма алгоритма
Для выполнения одной итерации требуется последовательно выполнить следующие действия:
- вычислить [math]\tau[/math] (2 операции сложения, 1 операция деления)
- вычислить [math]t[/math] (1 операция сравнения, 1 операция взятия модуля, 2 операции сложения, 1 операция умножения, 1 операция деления, 1 операция извлечения квадратного корня)
- вычислить [math]c[/math] (1 операция сложения, 1 операция умножения, 1 операция деления, 1 операция извлечения квадратного корня) и [math]s[/math] (1 операция умножения)
После этого выполняется ярус, отвечающий за применение поворота к матрице [math]A[/math] с параллельным выполнением [math]2(n-2)[/math] операций вычисления элементов матрицы [math]a_{jm}^{(i+1)} = a_{mj}^{(i+1)}[/math] и [math]a_{km}^{(i+1)} = a_{mk}^{(i+1)}[/math], [math]m \ne j,k[/math] , а также 2 операций вычисления элементов [math]a_{jj}^{(i+1)} [/math] и [math]a_{kk}^{(i+1)} [/math]. Наибольшее количество операций содержится в вычислении последних двух элементов (по 6 умножений и 3 сложения).
Суммарное количество итераций зависит от входных данных и заданного значения погрешности. Один "цикл" (полный проход по внедиагональным элементам) осуществляется за [math]N = \frac{n(n-1)}{2}[/math] итераций. Асимптотически метод сходится квадратично [2]. Как правило, для сходимости метода Якоби требуется от 5 до 10 циклов, что хуже, чем у конкурирующих алгоритмов [1].
Таким образом, при классификации по высоте ЯПФ метод Якоби относится к алгоритмам со сложностью [math]O(n^2)[/math] , а при классификации по ширине ЯПФ — к алгоритмам со сложностью [math]O(n)[/math].
1.9 Входные и выходные данные алгоритма
Входные данные: матрица [math]A[/math] (элементы [math]a_{ij}[/math]). Дополнительные ограничения:
- [math]A[/math] – симметрическая матрица, т. е. [math]a_{ij}= a_{ji}, i, j = 1, \ldots, n[/math].
Объём входных данных: [math]\frac{n (n + 1)}{2}[/math] (в силу симметричности достаточно хранить только диагональ и над/поддиагональные элементы). В разных реализациях эта экономия хранения может быть выполнена разным образом.
Выходные данные: вектор собственных значений [math]\Lambda[/math] (элементы [math]\lambda_{ii}[/math]).
Объём выходных данных: [math] n [/math].
1.10 Свойства алгоритма
Метод Якоби является самым медленным из имеющихся алгоритмов вычисления собственных значений симметричной матрицы. Тем не менее, он способен вычислять малые собственные числа и отвечающие им собственные векторы с гораздо большей точностью, чем другие методы [1]. Кроме того, он не предполагает первоначального приведения матрицы к трехдиагональной форме.
Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов для метода Якоби является линейным.
Вычислительная мощность алгоритма линейна.
Метод Якоби не детерминирован, так как является итерационным алгоритмом с выходом по точности: число итераций зависит от входных данных и порогового значения.
Дуги информационного графа, исходящие из вершин, соответствующих вычислениям значений [math]c[/math] и [math]s[/math], образуют пучки рассылок линейной мощности.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
Исследование масштабируемости проводилось на суперкомпьютере "Ломоносов" Суперкомпьютерного комплекса Московского Государственного Университета имени М.В. Ломоносова. Алгоритм реализован на языке C++ с использованием средств MPI. Компиляция производилась с помощью команды mpicxx с использованием компилятора Intel с OpenMPI и библиотеки MKL. Были подключены следующие модули: openmpi/1.5.5-icc, intel/13.1.0, mkl/4.0.2.146. Программа была запущена в очередях test и regular4.
Значения изменяемых параметров запуска реализации алгоритма:
- число процессов: 2, 4, 8, 16, 32, 64;
- число элементов в матрице: 900, 3600, 8100, 14400, 22500, 32400, 44100, 57600, 72900, 90000.
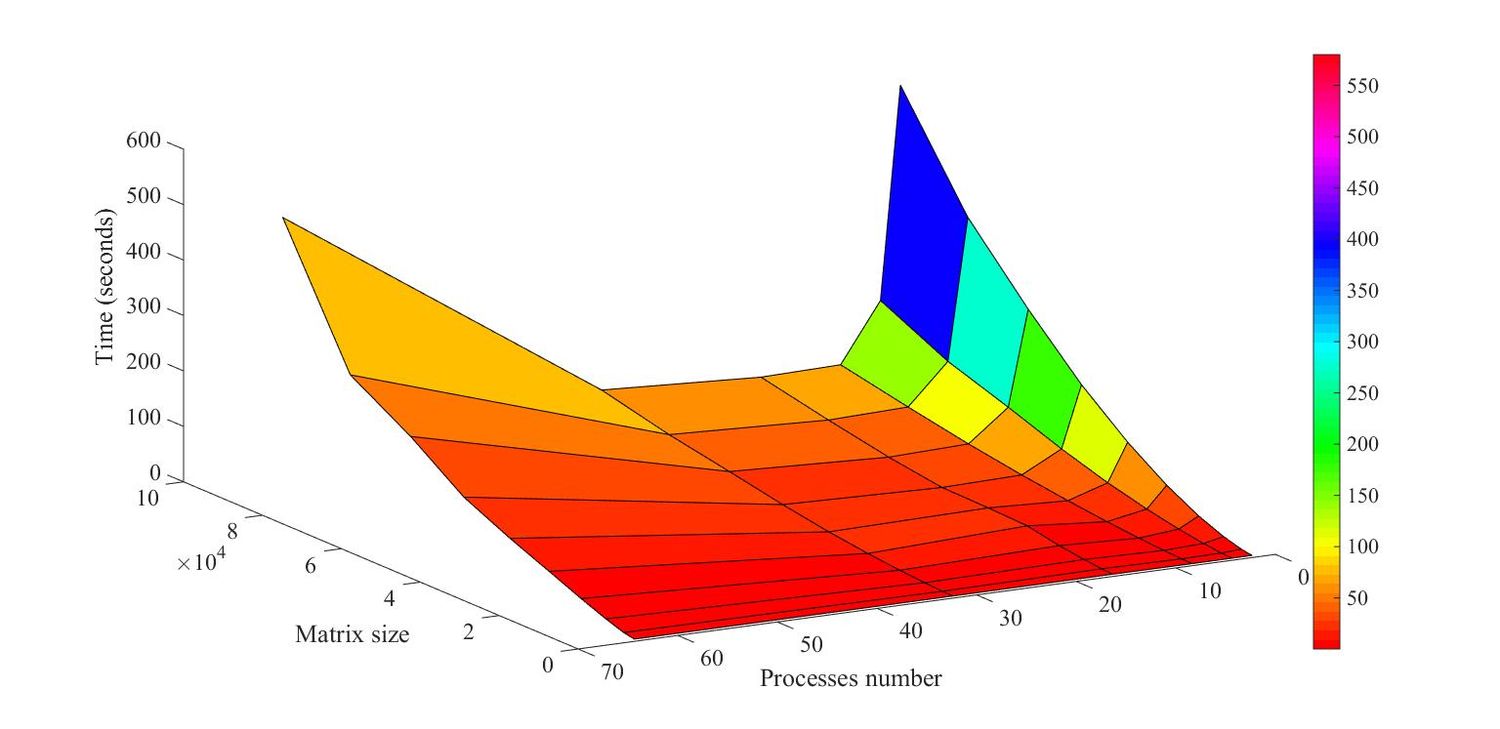
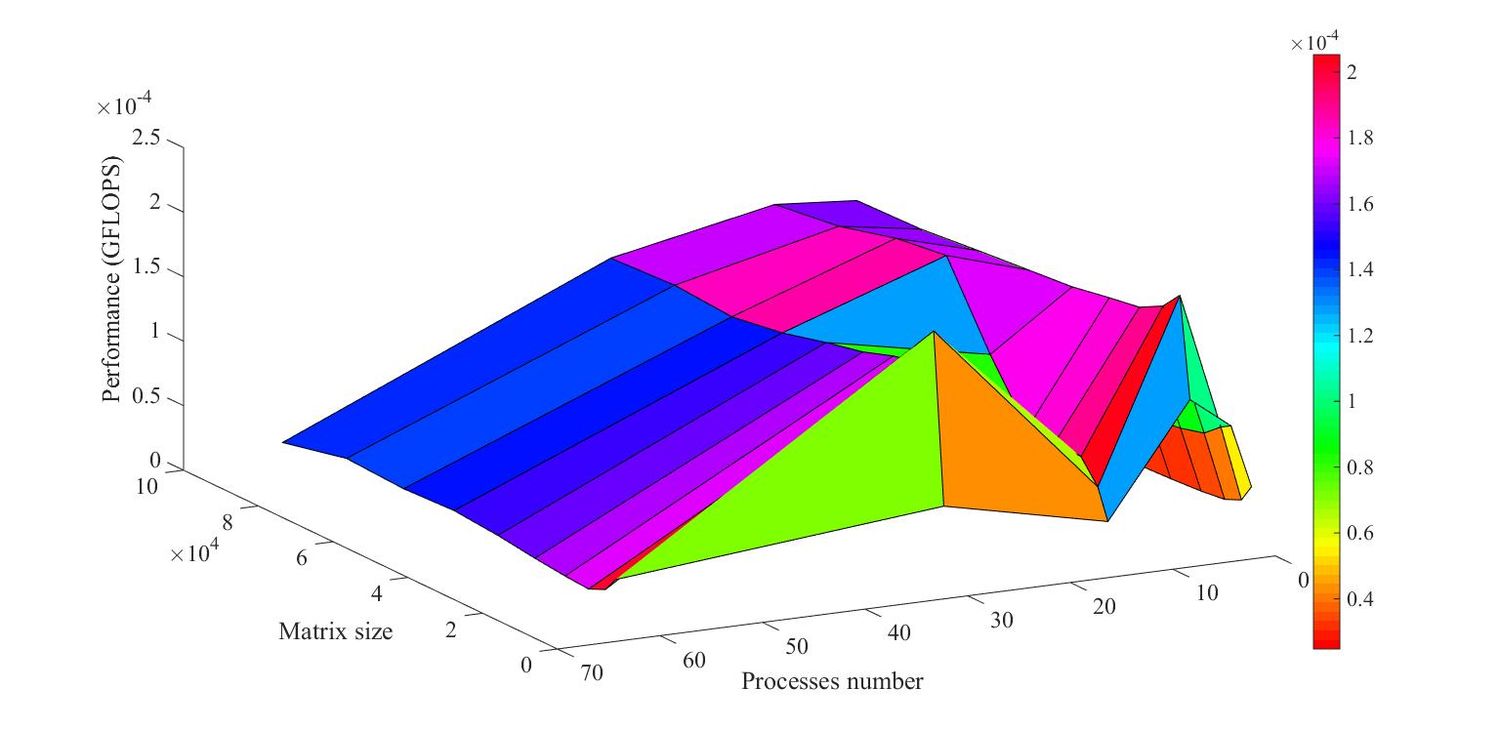
На следующих рисунках приведены графики времени выполнения и производительности выбранной реализации алгоритма в зависимости от изменяемых параметров запуска
На Рис.4 видно, что при увеличении количества процессов производительность сначала увеличивается, а затем уменьшается. Время работы алгоритма резко увеличивается при увеличении размеров матрицы, что обусловлено большим количеством сообщений, обрабатываемых корневым процессом. Полученные результаты говорят о плохой масштабируемости алгоритма.
Реализация алгоритма доступна по ссылке.
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
Существует библиотека JACOBI_EIGENVALUE, реализующая последовательный вариант метода Якоби на языках программирования С, С++, FORTRAN77, FORTRAN90, MATLAB, Python. Данная библиотека распространяется по лицензии GNU LESSER GENERAL PUBLIC LICENSE.
Существует также параллельная реализация метода на платформе CUDA.
3 Литература
<references \>