Участник:Odbaev/Нахождение собственных чисел квадратной матрицы методом QR разложения (2)

Эта работа прошла предварительную проверку Дата последней правки страницы: 07.11.2016 Данная работа соответствует формальным критериям. Проверено VadimVV.

Нахождение собственных чисел квадратной матрицы методом QR разложения
Последовательный алгоритм
Последовательная сложность	[math]N * O(n^3)[/math]
Объём входных данных	[math]n^2[/math]
Объём выходных данных	[math]n[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]N*(12n-15)[/math]
Ширина ярусно-параллельной формы	[math]O(n^2)[/math]

Основные авторы описания: О.Д.Баев (пп. 1.1 - 1.5, 2.4, 2.7), А.С.Шевелев (пп. 1.6 - 1.10)

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

QR-алгоритм — это численный метод в линейной алгебре, предназначенный для решения полной проблемы собственных значений, то есть отыскания всех собственных чисел и собственных векторов матрицы. Был разработан в конце 1950-х годов независимо В.Н. Кублановской и Дж. Фрэнсисом.

1.2 Математическое описание алгоритма

Пусть [math]A[/math] — вещественная квадратная матрица, для которой мы хотим найти собственные числа и векторы. Положим [math]A_0 = A[/math]. На k-ом шаге (начиная с k = 0) вычислим QR-разложение [math]A_k = Q_k R_k[/math], где [math]Q_k[/math] — ортогональная матрица (то есть [math]Q_k^{T} = Q_k^{-1}[/math]), а [math]R_k[/math] — верхняя треугольная матрица. Затем мы определяем [math]A_{k+1} = R_k Q_k[/math].

Заметим, что

[math] A_{k+1} = R_k Q_k = Q_k^{-1} Q_k R_k Q_k = Q_k^{-1} A_k Q_k = Q_k^{T} A_k Q_k, [/math]

то есть все матрицы [math]A_k[/math] являются подобными и их собственные значения равны.

Пусть все диагональные миноры матрицы [math]A[/math] не вырождены. Тогда последовательность матриц [math]A_k[/math] при [math]k \rightarrow \infty[/math] сходится по форме к клеточному правому треугольному виду, соответствующему клеткам с одинаковыми по модулю собственными значениями.

Для того, чтобы получить собственные векторы матрицы, нужно перемножить все матрицы [math]Q_k[/math].

1.3 Вычислительное ядро алгоритма

Основными вычислительными ядрами алгоритма являются:

• QR-разложение матрицы [math]A_k = Q_k R_k[/math]
• Умножение плотных матриц [math]A_{k+1} = R_k Q_k[/math]

Существуют различные алгоритмы вычисления QR-разложения. Можно выделить такие, как метод Гивенса и метод Хаусхолдера.

Подробное описание вычислительных ядер содержится в соответствующих статьях, указанных в пункте 1.4 (Макроструктура алгоритма).

1.4 Макроструктура алгоритма

QR-алгоритм на каждой итерации использует следующие макрооперации:

1. QR-разложение
   • Метод Гивенса (вращений)
   • Метод Хаусхолдера (отражений)
2. Умножение матриц

1.5 Схема реализации последовательного алгоритма

QR-алгоритм является итерационным.

На каждой итерации [math] k [/math]:

1. Строится QR-разложение матрицы [math] A_k = Q_k R_k [/math]
2. Получается матрица [math] A_{k+1} = R_k Q_k [/math], используемая на следующей итерации

Алгоритм выполняется до сходимости матрицы [math] A_k[/math] к треугольному виду.

Псевдокод алгоритма:

algorithm QR is
  input: Matrix A
  output: Eigenvalues of the matrix A
    
  repeat
    Q, R ← QR_factorization(A)
    A ← R×Q
  until convergence
    
  return diag(A)

1.6 Последовательная сложность алгоритма

Пусть дана матрица [math] A \in \mathbb{R}^{n \times n}[/math]. До момента приведения матрицы к треугольной форме произведено [math]N[/math] итераций алгоритма. На каждой итерации алгоритма производится три действия: QR-разложение, перемножение матриц и проверка, является ли матрица треугольной.

Распишем последовательную сложность каждого действия:

• QR-разложение:
  • Методом Гивенса (вращений) - [math]2*n^3[/math].
  • Методом Хаусхолдера (отражений) - [math]\frac{4}{3}n^3[/math].
• Перемножение матриц - [math]n^3[/math] операций.
• Проверка, имеет ли матрица треугольную форму - [math]\frac{n^2 - n}{2}[/math] операций.

Таким образом, на каждой итерации последовательный алгоритм выполняет [math]O(n^3)[/math] операций. Для всего алгоритма потребуется выполнить [math]N * O(n^3)[/math] операций.

1.7 Информационный граф

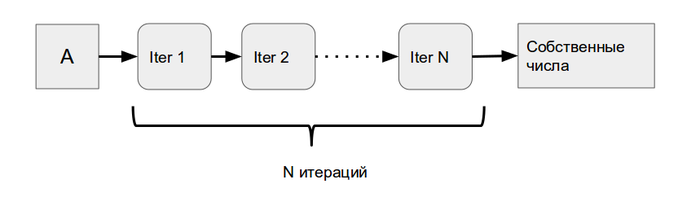
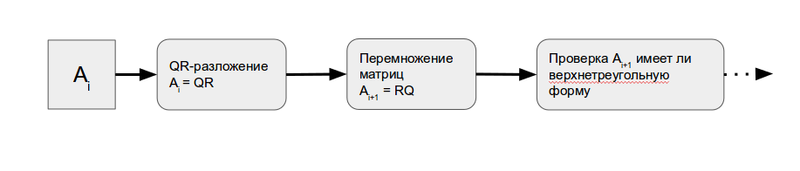
На Рисунке 1 изображен макрограф описываемого QR-алгоритма, представляющего собой последовательность итераций алгоритма. На рисунке 2 представлен граф, на котором более подробно отображено содержимое каждой итерации. Информационные графы QR-разложения и матричного умножения представлены в соответствующих статьях.

Рисунок 1. Макрограф базового QR-алгоритма.

Рисунок 2. Информационный граф i-й итерации QR-алгоритма.

1.8 Ресурс параллелизма алгоритма

Базовый алгоритм является итерационным и выполняется последовательно. Возможность распараллеливания алгоритма предоставляется при реализации операций таких, как QR-разложение, перемножение матриц и проверка, имеет ли матрица треугольную форму.

Рассчитаем параллельную сложность для каждой из указанных операций:

• QR-разложение:
  • Методом Гивенса (вращений) - [math]11n - 16[/math].
  • Методом Хаусхолдера (отражений) - [math]O(n^2)[/math].
• Перемножение матриц - [math]n[/math].
• Проверка, имеет ли матрица треугольную форму - [math]1[/math].

Результирующая параллельная сложность одной итерации [math]12n-15[/math] (для метода вращений). А всего алгоритма из [math]N[/math] итераций - [math]N*(12n-15)[/math].

1.9 Входные и выходные данные алгоритма

Входные данные: плотная квадратная матрица [math]A[/math] размера [math]n[/math].

Объём входных данных: [math]n^2[/math].

Выходные данные: [math]n[/math] собственных чисел матрицы [math]A[/math].

Объём выходных данных: [math]n[/math].

1.10 Свойства алгоритма

Описанный алгоритм обладает следующими свойствами:

• Недетерминирован - не известно заранее число итераций алгоритма, которое необходимо произвести до момента схождения матрицы к полностью треугольной форме или с некоторым значением точности.
• Скорость сходимости зависит от собственных чисел. Чем ближе собственные числа друг к другу, тем ниже скорость сходимости.
• Может быть хорошо распараллелен, так как соотношение последовательной и параллельной сложности алгоритма является квадратичным.
• Перемещение данных необходимых для выполнения алгоритма не затратно, так как вычислительная мощность [math] = \frac{N * O(n^3)}{n^2 + n}[/math] (отношение числа операций к суммарному объему входных и выходных данных) линейна на каждой итерации.

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

Используется процедура PDHSEQR из библиотеки ScaLAPACK.

Вычисления производились на суперкомпьютере Regatta.

Время работы алгоритма

Процессы\Матрица	600	1200	1800	2400
1	4.30549	25.2566	78.0507	177.054
4	3.63899	17.6559	51.2146	127.386
9	3.81662	9.19687	23.9181	53.7105
16	3.11883	7.26239	16.0958	32.3561

Реализация алгоритма

2.7 Существующие реализации алгоритма

Полный алгоритм:

• LAPACK: функция DGEEV (последовательная реализация)
• ScaLAPACK: функция PDHSEQR (параллельная реализация)
• ALGLIB: реализация алгоритма для различных языков программирования
• Python NumPy: функции linalg.eig, linalg.eigvals
• C++ Eigen: Eigenvalues модуль

QR-разложение:

• LAPACK: функция DGEQRF (последовательная реализация)
• ScaLAPACK: функция PDGEQRF (параллельная реализация)
• MATLAB: функция qr
• Mathematica: функция QRDecomposition
• ALGLIB: реализация QR-разложения для различных языков программирования
• Python NumPy: функция linalg.qr
• C++ Eigen: QR модуль

Умножение матриц:

• LAPACK: функция DGEMM (последовательная реализация)
• ScaLAPACK: функция PDGEMM (параллельная реализация)
• MATLAB: функции mtimes, *
• Mathematica: функция Dot
• Python NumPy: функция numpy.dot