Участник:RS42/Quickhull

Тимофеев Александр Евгеньевич, группа 403

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Задача построения выпуклой оболочки является одной из важных проблем вычислительной геометрии. Выпуклую оболочку множества точек [math]X[/math] можно определить следующим образом: это пересечение всевозможных выпуклых множеств, содержащих [math]X[/math]. В случае конечного числа [math]n[/math] точек из [math]X[/math]:

[math]\mathrm{Conv}(X)=\left\{\left.\sum_{i=1}^{n} \alpha_i x_i\ \right| (\forall i: \alpha_i\ge 0)\wedge \sum_{i=1}^{n} \alpha_i=1 \right\}.[/math]

Алгоритм Quickhull позволяет провести построение в пространстве произвольной размерности [math]d[/math]. Результатом работы является множество [math]d-1[/math]-мерных граней (facets) и вершин (vertices) полученной выпуклой оболочки.

1.2 Математическое описание алгоритма

Наложим на множество [math]X[/math] следующее условие: любые [math]d+1[/math] точки аффинно независимы (что тождественно тому, что они не лежат в одной [math]d-1[/math]-мерной плоскости). Выпуклая оболочка будет задаваться списком вершин и граней. Для каждой грани известны ее вершины, ее соседние грани и уравнение гиперплоскости, в которой эта грань лежит. Ребро (ridge) определяется как пересечение двух соседних граней и имеет размерность [math]d-2[/math]. Граница грани состоит из ребер.

Нам понадобится вычисление ориентированного расстояния от некоей точки [math]x[/math] до гиперплоскости (signed distance to hyperplane). Зададим начало координат в точке [math]O[/math], плоскость определяется единичной нормалью [math]\vec n[/math] и смещением [math]h[/math] относительно начала координат. Тогда ориентированное расстояние будет равно [math](\vec x, \vec n) + h[/math], где [math]\vec x = x - O[/math]. Точки на гиперплоскости удовлетворяют, собственно говоря, ее уравнению [math](\vec x, \vec n) + h = 0 [/math]. Если ориентированное расстояние положительно, то можно сказать, что точка находится выше плоскости (или плоскость видна из точки). В нашем случае все грани выпуклой оболочки во время построения будут иметь такие нормали и смещения, что для точек внутри оболочки расстояния до каждой плоскости будут неположительными.

Рассмотрим сам алгоритм:

создать начальный d-симплекс
для каждой грани F
  для каждой нераспределенной точки p
    если p находится над F
      добавить p во множество внешних точек грани F
для каждой грани F с непустым множеством внешних точек
  выбрать наиболее отдаленную точку p из списка внешних точек грани F
  добавить F во множество видимых граней V
  для каждого непосещенного соседа N для граней из V
    если N видна из p
      добавить N в V
  граница множества V будет набором граничных ребер H
  для каждого ребра R из H
    построить новую грань из R и p
     соединить построенную грань с ее соседями
  для каждой новой грани G
    для каждой нераспределенной точки q из объединения множеств внешних точек граней из V
      если G видна из q
        добавить q во множество внешних точек G
  удалить грани из V

Стартовый симплекс, который по ходу работы алгоритма будет расти до окончательной оболочки, можно создать из любых [math]d+1[/math] точек, исходя из условия на [math]X[/math]. Но в реальности это условие общего положения (general position) можно заменить на требование возможности выбрать [math]d[/math]-мерный симплекс. Имеет смысл выбрать его таким образом, чтобы как можно больше точек уже оказалось в нем, поэтому его вершинами следует сделать точки с минимальными и максимальными координатами. Если таких точек не будет хватать, произведем добор произвольными.

Дальнейшие шаги алгоритма позволяют добавлять к промежуточной выпуклой оболочке новые вершины. По сути выбирается оптимальная в каком-то смысле внешняя точка [math]p[/math], а затем определяется множество [math]V[/math] видимых из этой точки граней. Данные видимые грани отделены от невидимых множеством граничных ребер (horizon ridges). Далее граничные ребра и точка [math]p[/math] образуют новые грани, видимые грани удаляются. Тем самым совершен переход к новой промежуточной выпуклой оболочке. Такое описание является обобщенным и ему также соответствует randomized incremental algorithm, в котором точка [math]p[/math] выбирается случайным образом. В нашем случае точка [math]p[/math] будет наиболее отдаленной точкой от плоскости текущей рассматриваемой грани [math]F[/math], что однако же не гарантирует присутствие [math]p[/math] в итоговой выпуклой оболочке. Также можно выбрать [math]p[/math] как наиболее отдаленную точку среди всех пар (грань-"самая дальняя точка этой грани"), но такой выбор на каждом шаге только увеличит время работы алгоритма.

Как решается проблема определения граничных ребер, когда уже выбрана точка [math]p[/math]? Множество внешних точек (outside set) грани [math]F[/math] представляет из себя множество точек (возможно не всех), из которых эта грань видна. Поэтому если [math]p[/math] из множества внешних точек грани [math]F[/math], то это означает, что [math]F[/math] будет видна из [math]p[/math], и следует начать поиск границы именно с соседей [math]F[/math]. Пусть [math]H[/math] - соседняя к [math]F[/math] грань. Если [math]H[/math] видна, то следует проверить таким же образом и соседей [math]H[/math]. Если [math]H[/math] не видна, то мы наткнулись на участок границы, и рассматривать соседей [math]H[/math] нет смысла.

Получив граничные ребра, строим новые грани. Требуется обновить списки соседей и понять, какие внешние точки были захвачены. Захватить мы могли только те точки, которые были внешними для уничтоженных на этом шаге граней. То есть множество таких точек - это объединение множеств внешних точек граней из [math]V[/math]. Распределяем эти точки по множествам внешних точек для новых граней.

Алгоритм будет продолжать свою работу до тех пор, пока не останется ни одного пустого множества внешних точек.

1.3 Вычислительное ядро алгоритма

В алгоритме можно выделить две трудоемкие части:

1. Распределение точек по множествам внешних точек.

Элементарная операция на данном этапе - вычисление расстояния от точки до плоскости, сложность [math]O(d)[/math].

2. Построение новых граней.

Основная операция - нахождение гиперплоскости по точкам, сложность [math]O(d^3)[/math]. На практике также присутствуют расходы по работе со структурами данных, представляющих выпуклую оболочку.

1.4 Макроструктура алгоритма

Рассмотрим подробнее процесс построения новой грани. Она получается путем взятия одного ребра ([math]d-1[/math] точка) из множества граничных ребер и прибавлением к этому ребру выбранной на данном этапе вершины. Тем самым возможно определение [math]d-1[/math] нового ребра, которые вместе с исходным составляют одну грань. Но полученные ребра также принадлежат и другим граням из строящегося конуса, которые попарно граничат с текущей гранью как раз по каждому из ребру. Для отслеживания уже построенных ребер можно использовать хэш-таблицу. Нахождение уравнения гиперплоскости по точкам [math]{x_i}, i=1,..,d[/math] может сводиться к решению системы [math]An=0[/math], где [math]A[/math] - матрица размера [math](d-1) \times d[/math], строки которой представляют из себя транспонированные векторы [math]x_i-x_1 , i=2,..,d[/math]. Например, это можно сделать с помощью [math]LUP[/math]. Затем несложно отыскать [math]f=-(n,x_1)[/math]. Далее следует убедиться, что ориентированное расстояние для точек внутри выпуклой оболочки будет отрицательно, для этого используется некая точка [math]c[/math], заведомо лежащая внутри. Ее можно выбрать в самом начале в качестве среднего значения точек начального симплекса.

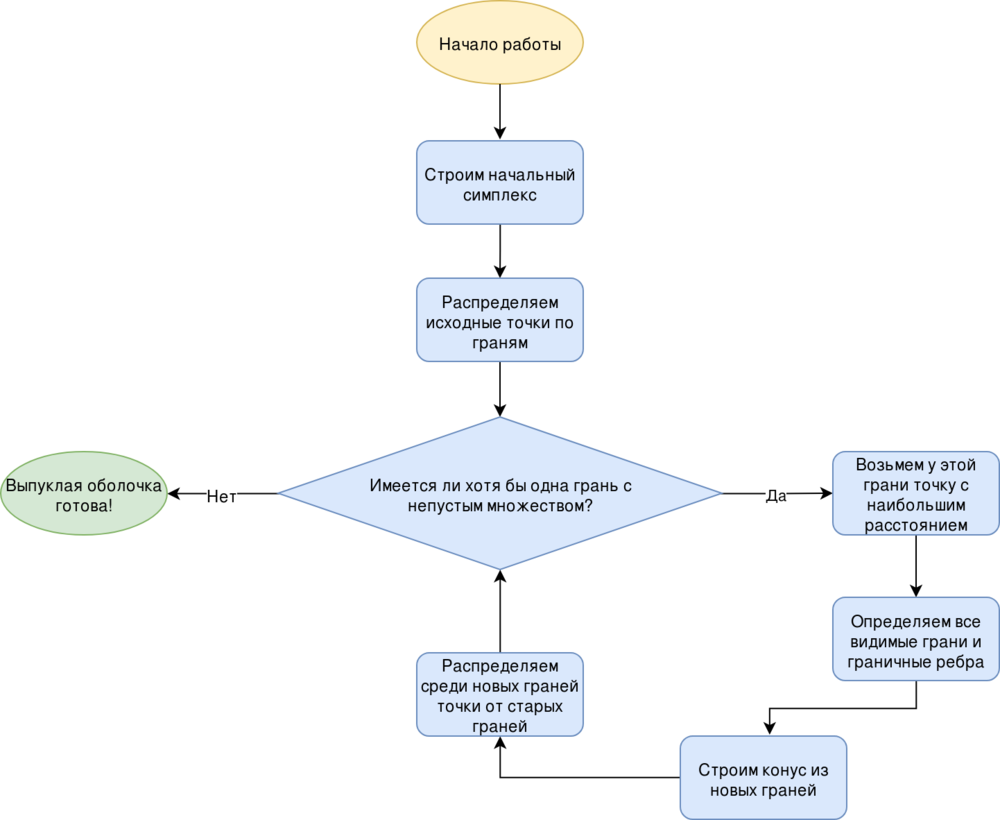
1.5 Схема реализации последовательного алгоритма

1.6 Последовательная сложность алгоритма

Обозначим за [math]r[/math] число вершин итоговой выпуклой оболочки, а [math]f_r[/math] примем за максимальное число граней для [math]r[/math] вершин. Известно, что [math]f_r = O(r^{\lfloor d/2 \rfloor}/ \lfloor d/2 \rfloor!)[/math].

Авторы алгоритма приводят верхнюю оценку сложности для так называемого сбалансированного случая, и она составляет [math]O(n \ log \ r) [/math] при [math]d \leq 3[/math] и [math]O(n f_r / r)[/math] при [math]d \geq 4 [/math].

2 Программная реализация алгоритма

2.7 Существующие реализации алгоритма

На момент написания данной статьи о существовании реализации алгоритма с помощью средств параллельных вычислений ничего неизвестно. В данной статье предложена реализация с использованием CUDA.

Последовательные реализации:

• Qhull - каноничная реализация от авторов алгоритма, обладающая широкими возможностями. Есть готовые пакеты во многих дистрибутивах.
• https://github.com/tomilov/quickhull - более компактная реализация на C++, описание доступно в виде статьи.

3 Литература

• Barber, C.B., Dobkin, D.P., and Huhdanpaa, H.T., "The Quickhull algorithm for convex hulls," ACM Trans. on Mathematical Software, 22(4):469-483, Dec 1996, http://www.qhull.org
• Clarkson , K. L., Mehlhorn , K., and Seidel , R. 1993. Four results on randomized incremental constructions. Comput. Geom. Theory Appl. 3, 185–211. Also in Lecture Notes in Computer Science. Vol. 577, pp. 463– 474.