Участник:Timokhinivan/Быстрое преобразование Фурье: различия между версиями
| Строка 160: | Строка 160: | ||
Таким образом, с учётом разложения <math>N</math>, <math>h(N) = O\left(\sum_{i=1}^K p_i\right) = O(P \log_P N) = O(\log N)</math>. | Таким образом, с учётом разложения <math>N</math>, <math>h(N) = O\left(\sum_{i=1}^K p_i\right) = O(P \log_P N) = O(\log N)</math>. | ||
| − | === | + | === Ресурс параллелизма алгоритма === |
Поскольку все рекурсивные вызовы преобразования Фурье на каждом из этапов совершенно | Поскольку все рекурсивные вызовы преобразования Фурье на каждом из этапов совершенно | ||
независимы, кажется естественным распределить их по доступным | независимы, кажется естественным распределить их по доступным | ||
Версия 18:21, 9 октября 2016
| Данная страница в настоящее время активно редактируется участником Timokhinivan (обсуждение). Пожалуйста, не вносите в неё никаких изменений до тех пор, пока не исчезнет это объявление. В противном случае могут возникнуть конфликты редактирования. |
| Быстрое преобразование Фурье | |
| Последовательный алгоритм | |
| Последовательная сложность | [math]O(N \log N)[/math] |
| Объём входных данных | [math]N[/math] |
| Объём выходных данных | [math]N[/math] |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | [math]O(\log N)[/math] |
| Ширина ярусно-параллельной формы | [math]O(N)[/math] |
Содержание
- 1 Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 TODO Входные и выходные данные алгоритма
- 1.10 TODO Свойства алгоритма
1 Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Преобразование Фурье переводит сигнал в его спектр и обратно, и широко применяется в самых различных областях вычислительной математики — собственно спектральный анализ, сжатие данных, вычисление свёрток и т.д. В связи с этим, особый интерес представляют быстры алгоритмы для вычисления этого преобразование. На сегодняшний день, наилучшие из них имеют сложность [math]O(n \log n)[/math].
1.2 Математическое описание алгоритма
Преобразование Фурье задаётся следующей формулой:
- [math] Y_k = \sum_{l = 0}^{N-1} X_l \epsilon^{kl}_N,\qquad k = \overline{0,N-1} [/math]
где [math]\epsilon_N = e^{\frac{2i\pi}{N}}[/math] — первообразный корень из 1 степени [math]N[/math].
Таким образом, преобразование Фурье является линейным и задаётся матрицей [math]F = \left\{ \epsilon^{kl}_N \right\}_{k\,l = 0}^{N-1}[/math].
1.2.1 Многомерное преобразование Фурье
Естественным обобщением описанного одномерного преобразования Фурье является многомерный вариант:
- [math] X(l_1,\cdots,l_d) = \sum_{k_1 = 0}^{N_1} \cdots \sum_{k_d = 0}^{N_d} Y(k_1,\cdots,k_d) \prod_{j=1}^{d} \epsilon_{N_j}^{l_j k_j} [/math]
Многомерное преобразование Фурье эквивалентно последовательному выполнению одномерных преобразований по каждому измерению; при использовании для этого рекурсивного алгоритма, общая сложность вычислений также составляет [math]O(N\log N)[/math], [math]N = \prod_{j=1}^d N_j[/math].
1.2.2 Сведение к двумерному преобразованию
Если [math]N[/math] — составное, т.е. [math]N = mn[/math], то возможно существенно сократить вычислительные расходы за счёт сведение к двумерному преобразованию Фурье. А именно, положим [math]X(l_1, l_2) = X_{l_1 n + l_2}[/math], [math] Y(k_1, k_2) = Y_{k_1 m + k_2}[/math], где [math]l_1, k_2 = \overline{0, m-1}[/math], [math]l_2, k_1 = \overline{0, n-1}[/math].
В этом случае
- [math] \begin{align} Y(k_1, k_2) &=& \sum_{l_2=0}^{n-1} (\epsilon^{k_2 l_2}_N \hat{X}(k_2, l_2)) \epsilon^{k_1 l_2}_n \\ \hat{X}(k_2, l_2) &=& \sum_{l_1=0}^{m-1} X(l_1, l_2) \epsilon^{k_2 l_1}_m \end{align} [/math]
Это даёт следующий алгоритм вычисления преобразования:
- Записываем исходный вектор в матрицу [math]m\times n[/math] по строкам.
- Применяем к каждому столбцу преобразование Фурье.
- Умножаем элемент в позиции [math](i,j)[/math] на [math]\epsilon^{ij}_N[/math].
- Применяем к каждой строке преобразование Фурье.
- Результат записан в получившейся матрице по столбцам.
Данный алгоритм уже даёт существенный выигрыш по сравнению с обычным умножением матрицы на вектор: [math] O(m^2 n + n^2 m) [/math] против [math]O(m^2 n^2)[/math]. Однако наилучших результатов можно добиться, если применять этот алгоритм рекурсивно на этапах 2 и 4.
Так, если [math]N = \prod_{i=1}^{K} p_i[/math], то целесообразно на каждом уровне рекурсии «отщеплять» одно [math]p_i[/math]. В этом случае задача сводится к вычислению [math] \prod_{i\neq j} p_i [/math] преобразований Фурье порядка [math]p_j[/math] для всех [math]j[/math]. При небольших [math]p_i[/math] (например, 2), это можно проделывать «в лоб».
1.3 Вычислительное ядро алгоритма
На каждом уровне рекурсии наиболее дорогостоящими этапами являются рекурсивные вызовы преобразования Фурье: они требуют в сумме [math]O(mn (\log m + \log n))[/math] операций против [math]O(mn)[/math] для умножения на поправочные коэффициенты (шаг 3).
То же верно и для алгоритма в целом в случае [math]N = \prod_{i=1}^{K} p_i[/math]; а именно, суммарно наибольшие вычислительные затраты связаны с вычислением преобразований Фурье порядка [math]p_i[/math].
1.4 Макроструктура алгоритма
Фактически, макроструктура алгоритма уже описана в разделе математического описания. На каждом уровне рекурсии, алгоритм состоит из
- [math]n[/math] рекурсивных вызовов алгоритма.
- Умножение всех элементов рабочего вектора на поправочные коэффициенты.
- Ещё [math]m[/math] рекурсивных вызовов.
1.5 Схема реализации последовательного алгоритма
Псевдокод:
fft(X, N)
begin
(m, n) = factor(N)
if (n == 1) // Предполагается, что n <= m
direct_fft(X, N) // Через умножение на матрицу
// 1
transpose(X, m, n) //Транспонирует X как матрицу m x n, хранящуюся по строкам
// 2
do i = 0, n - 1
fft(X(i * m : (i + 1) * m - 1), m)
// 3
do i = 0, n - 1
do j = 0, m - 1
X(i * m + j) *= eps(i * j, N)
// 4
transpose(X, n, m)
// 5
do j = 0, m - 1
fft(X(j * n : (j + 1) * n - 1), n)
// 6
transpose(X, m, n)
end
Здесь eps может как вычислять соответствующие коэффициенты, так и брать их из заранее заготовленной таблицы. Последний способ требует увеличения затрат по памяти, но позволяет существенно сэкономить на вычислениях, а потому является предпочтительным.
Кроме того, шаги 3 и 4 можно переставлять произвольным образом (с очевидными изменениями в шаге 3).
1.6 Последовательная сложность алгоритма
Непосредственно из описания алгоритма получаем, что если сложность вычисления преобразования Фурье обозначить [math]f_N[/math], то [math]f_{mn} = n f_{m} + m f_{n} + mn[/math].
Если [math]N = \prod_{i=1}^K p_i[/math], и на каждом шаге «отщеплять» от него одно [math]p_i[/math], а преобразование Фурье для [math]p_i[/math] вычислять «в лоб», то общее количество операций составит [math]O\left(N\sum_{i=1}^K p_i\right)[/math].
В частности, если [math]p_i \leq P[/math], то [math]K \leq \log_P N[/math] и для сложности получаем [math]O(NP\log_P N)[/math]. Полагая [math]P[/math] фиксированным, получаем заявленную сложность [math]O(N \log N)[/math].
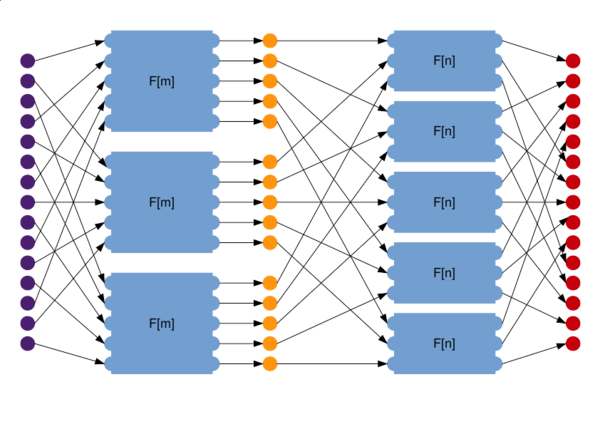
1.7 Информационный граф
Каждый уровень рекурсивного вызова состоит из трёх этапов: рекурсивный вызов по столбцам, умножение на поправочные коэффициенты и рекурсивного вызова по строкам. Таким образом для высоты ЯПФ имеем
- [math] h(mn) = 1 + h(m) + h(n) [/math]
Для «элементарных» БПФ высота ЯПФ будет та же, что и для умножения матрицы на вектор.
Таким образом, с учётом разложения [math]N[/math], [math]h(N) = O\left(\sum_{i=1}^K p_i\right) = O(P \log_P N) = O(\log N)[/math].
1.8 Ресурс параллелизма алгоритма
Поскольку все рекурсивные вызовы преобразования Фурье на каждом из этапов совершенно независимы, кажется естественным распределить их по доступным вычислительным узлам. Умножение на поворотные коэффициенты при этом и вовсе выполняется независимо на каждом элементе рабочего вектора, и может быть беспрепятственно присоединёно к любому из этапов.
При этом, в отличие от традиционной реализации типа Кули-Тьюки, в которой на каждом этапе один из множителей берётся малым, при параллельной реализации целесообразно взять и [math]m[/math] и [math]n[/math] по возможности близкими к кратным доступному количеству вычислительных узлов, поскольку в этом случае возможно равномерно распределить работу между ними и реализовать весь алгоритм всего с одной внутренней пересылкой.
1.9 TODO Входные и выходные данные алгоритма
В общем случае на входе и на выходе имеются комплексные векторы порядка [math]N[/math].