Уровень алгоритма

Учacтник:Malikovmt/Алгоритм Ланцоша для арифметики с плавающей точкой с полной переортогонализацией: различия между версиями

Материал из Алговики
Перейти к навигации Перейти к поиску
[непроверенная версия][непроверенная версия]
 
(не показана 41 промежуточная версия 2 участников)
Строка 1: Строка 1:
 +
{{Assignment|ASA}}
 +
 
{{algorithm
 
{{algorithm
 
| name              = Алгоритм Ланцоша с полной переортогонализацией
 
| name              = Алгоритм Ланцоша с полной переортогонализацией
−
| serial_complexity = <math>O(n^2k + nk^2)</math>
+
| serial_complexity = <math>O(n^2k)</math>
−
| pf_height        = <math>O(nk + k^2)</math>
+
| input_data        = <math>\frac{n(n + 1)}{2}</math>
−
| pf_width          = <math>O(n)</math>
+
| output_data      = <math>k(n + 1)</math>
−
| input_data        = <math>n^2 + n</math>
 
−
| output_data      = <math>2k - 1 + nk</math>
 
 
}}
 
}}
  
Строка 14: Строка 14:
 
=== Общее описание алгоритма ===
 
=== Общее описание алгоритма ===
  
−
'''Алгоритм Ланцоша''' - итерационный метод, используемый для вычисления части собственных значений и соответствующих им собственных векторов матрицы <math>A</math> размера <math>n*n</math>, изначально разработанный Корнелием Ланцошем. Преимуществами использования метода является относительно небольшое потребление памяти и вычислительных ресурсов, а также наличие параметра <math>m</math>, контролирующего количество итераций. Несмотря на то, что алгоритм является вычислительно эффективным, первоначально сформулированный метод был плохо применим из-за численной неустойчивости - метод хорошо работал на целочисленных значениях, однако в арифметике с плавающей точкой ошибки округления давали большую погрешность. В 1970 году Ojalvo и Newman показали, как сделать метод численно стабильным и применили его для расчета крупных инженерных сооружений, подверженных динамическим нагрузкам. Кроме того, они показали способ выбора начального приближения (с использованием ГПСЧ), а также эмпирический способ для нахождения числа <math>m</math> (примерно в полтора раза больше искомого числа собственных векторов). В данный момент существует две основных модификации метода (с полной и выборочной переортогонализацией), а также большое количество модификаций, использующихся в различных технических областях.
+
'''Алгоритм Ланцоша''' - итерационный метод, используемый для вычисления части собственных значений и соответствующих им собственных векторов матрицы <math>A</math> размера <math>n*n</math>, изначально разработанный Корнелием Ланцошем. Преимуществами использования метода является относительно небольшое потребление памяти и вычислительных ресурсов, а также наличие параметра <math>k << n</math>, контролирующего количество итераций. Несмотря на то, что алгоритм является вычислительно эффективным, первоначально сформулированный метод был плохо применим из-за численной неустойчивости - метод хорошо работал на целочисленных значениях, однако в арифметике с плавающей точкой ошибки округления давали большую погрешность. В 1970 году Ojalvo и Newman показали, как сделать метод численно стабильным и применили его для расчета крупных инженерных сооружений, подверженных динамическим нагрузкам. Кроме того, они показали способ выбора начального приближения (с использованием ГПСЧ), а также эмпирический способ для выбора числа <math>k</math> (примерно в полтора раза больше искомого числа собственных векторов). В данный момент существует две основных модификации метода (с полной и выборочной переортогонализацией), а также большое количество модификаций, использующихся в различных технических областях. Алгоритм используется для больших <math>n</math>.
  
 
=== Математическое описание алгоритма ===
 
=== Математическое описание алгоритма ===
 +
 +
Первый этап алгоритма - использование метода Ланцоша для построения крыловского подпространства: <math> K_k(A,x) = span[x_1, Ax_1, A^2x_1, ..., A^{k-1}x_1] </math>. Входные данные алгоритма: квадратная симметричная матрица <math>A</math> размерности <math>n*n</math>, вектор начального приближения <math>b</math>, а так же число итераций <math>k</math>. Метод осуществляет поиск трехдиагональной симметричной матрицы <math>T_k=Q_k^TAQ_k</math>.
 +
 +
<math>T_k=\begin{bmatrix}
 +
\alpha_1 & \beta_2 \\
 +
\beta_2 & \alpha_2 & \beta_3 &\\
 +
&. & . & .\\
 +
&&\beta_{k-1} & \alpha_{k-1} & \beta_k\\
 +
&&&\beta_k & \alpha_k
 +
\end{bmatrix}</math>
 +
 +
Описание метода:
 +
 +
<math>
 +
\begin{array}{l}
 +
q_1 = b / \Vert b \Vert_2\\
 +
j = \overline{1, k}:\\
 +
\quad z_j = A q_j \\
 +
\quad \alpha_j = q_j^T z_j \\
 +
\quad z_j = z_j - \sum_{i=1}^j (z_j^T q_i) q_i\\
 +
\quad z_j = z_j - \sum_{i=1}^j (z_j^T q_i) q_i\\
 +
\quad \beta_j = \Vert z_j \Vert_2\\
 +
\quad q_{j+1} = z_j / \Vert z_j \Vert_2 = z_j/\beta_j
 +
\end{array}
 +
</math>
 +
 +
Следующий шаг алгоритма - процедура Рэлея-Ритца. Она зкалючается в интерпретации собственных значений матрицы <math> T_k=Q_k^TAQ_k</math>.
 +
Ее собственные значения приближают собственные значения исходной матрицы. Пусть ''T<sub>k</sub>=V<math>\Lambda</math>V<sup>T</sup>'' - спектральное разложение матрицы ''T<sub>k</sub>'', тогда столбцы матрицы ''Q<sub>k</sub>V'' рассматриваются как приближения к соответствующим собственным векторам матрицы ''A'' и называются векторами Ритца. Числа и векторы Ритца являются оптимальными приближениями к собственным значениям и собственным векторам матрицы ''A''.
 +
 +
Поиск собственных значений матрицы ''T'' намного легче, чем для исходной матрицы, так как предполагается, что <math>k << n</math>, и матрица ''T'' - трехдиагональная.
 +
 +
Полная переортогонализация необходима для того, чтобы гарантировать, что каждый полученный вектор ''q<sub>j+1</sub>'' ортогонален уже имеющимся векторам ''q<sub>1..j</sub>''. Без этого процесса будут накапливаться существенные вычислительный ошибки.
  
 
=== Вычислительное ядро алгоритма ===
 
=== Вычислительное ядро алгоритма ===
 +
 +
Вычислительным ядро алгоритма состоит ииз двух основных частей:
 +
* <math>Aq=( \sum\nolimits_{i=^n}a_{1i}q_i, \sum\nolimits_{i=2}^na_{2i}q_i, ..., \sum\nolimits_{i=1}^na_{ni}q_i)</math> - умножение симметричной матрицы <math>A</math> размерности <math>n*n</math> на вектор ''q'' размерности ''n''.
 +
 +
* <math>z=z-\sum\nolimits_{i=1}^{k}(z^Tq_i)q_i.</math> - процесс ортогонализации Грама-Шмидта.
  
 
=== Макроструктура алгоритма ===
 
=== Макроструктура алгоритма ===
 +
Основные операции алгоритма:
 +
 +
1. Перемножение матрицы на вектор.
 +
<math>b=Ax</math>.
 +
 +
2. Двойная ортогонализация методом Грмма-Шмидта.
 +
<math>z=z-\sum\nolimits_{i=1}^{j-1}(z^Tq_i)q_i,</math>
 +
<math>z=z-\alpha_jq_j-\beta_{j}q_{j-1}.</math>
 +
 +
3. Вычисление обновленного базисного вектора.
 +
<math>q_{i+1} = z/ \beta</math>.
  
 
=== Схема реализации последовательного алгоритма ===
 
=== Схема реализации последовательного алгоритма ===
 +
 +
В параграфе 1.2 приводится полная схема последовательного алгоритма.
 +
 +
Заполняем начальные значения алгоритма (''b'' - начальное преближение).
 +
 +
<math>
 +
\begin{align}
 +
& q_1=b/||b||,\\
 +
& \beta_1=0,\\
 +
&q_0=0, \\
 +
\end{align}
 +
</math>
 +
 +
Для всех <math>j=1..k</math>:
 +
 +
*1. Вычисляется ''j''-й диагональный элемент матрицы <math>T_k</math>: <math>z=Aq_j; \alpha_j=q_j^Tz;</math>
 +
 +
*2. Проводится полная переортогонализация Грамма-Шмидта: <math>z =z-\sum\nolimits_{i=1}^{j-1}(z^Tq_i)q_i;</math>
 +
 +
*3. Вычисляются значения <math>\beta_{j+1}</math> матрицы <math>T_k</math>: <math>\beta_{j+1}=||z||;</math>
 +
 +
*4. Если <math>\beta_{j+1}=0</math>, то алгоритм завершается;
 +
 +
*5. Сохраняем значения для следующей итерации <math>q_{j+1}=z/\beta_{j+1}.</math>
  
 
=== Последовательная сложность алгоритма ===
 
=== Последовательная сложность алгоритма ===
 +
 +
*1. Основная часть операций в алгоритме Ланцоша производится во время умножения матрицы <math>A</math> размерности <math>n*n</math> на вектор <math>q</math> размерности <math>n</math> - вычислительная сложность: <math>n^2</math> умножений и <math>n^2-n</math> сложений. Остальные операции основного цикла производят меньше <math>n^2</math> операций сложения или умножения. Так как умножение матрицы на вектор производится <math>k</math> раз, то сложность этой части алгоритма - <math>O(kn^2)</math>
 +
*2. Процесс ортогонализации Грама-Шмидта - вычислительная сложность: <math>k^2n+k(n+2)</math> умножений и <math>k^2n + k(n + 1) + 2</math> сложений. Производится в цикле <math>k</math> раз. Сложность - <math>O(nk^2)</math>
 +
*3. Процесс разложения матрицы <math>T</math> размерности <math>k*k</math>. Сложность - <math>O(k^2)</math>
 +
 +
Так как число итераций много меньше размерности матрицы <math>A</math>, <math>k << n</math>, то общая сложность алгоритма сокращается до <math>O(kn^2)</math>.
  
 
=== Информационный граф ===
 
=== Информационный граф ===
 +
 +
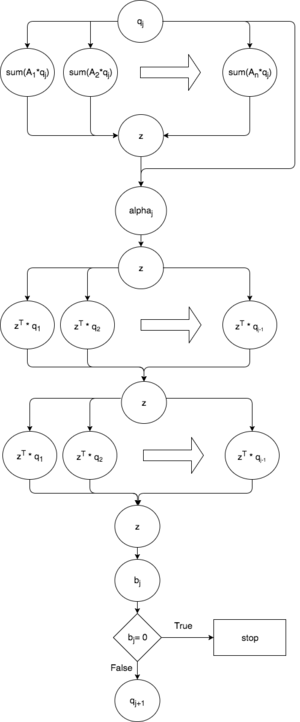
[[Файл:Lanczos.png|center|300px|'''Рис. 1.''' Граф ''j''-й итерации.]]
 +
 +
Черные маленькие стрелочки - куда идут данные.
 +
 +
Большие стрелочки - обозначение прохода по массиву (изменение индекса)
 +
 +
В больших кружках преобразования (операции над данными или вычисления)
 +
 +
В маленьких кружках запись в переменную.
  
 
=== Ресурс параллелизма алгоритма ===
 
=== Ресурс параллелизма алгоритма ===
 +
 +
Алгоритм Ланцоша - итерационный, итерации должны выполняться в строгой последовательности, и нет возможности их параллелизовать. Внутри одной итерации алгоритма ресурсами параллелизма могут быть:
 +
*1. умножение матрицы размерности <math>n * n</math> на вектор длины <math>n</math> требует последовательного выполнения <math>n</math> ярусов умножений и сложений;
 +
*2. вычисление <math>\alpha_j</math> требует <math>n</math> ярусов сложений с 1 операцией умножения в каждом;
 +
*3. переортагонализация требует вычисления <math>j</math> ярусов сложений с <math>n</math> операциями умножения в каждом, <math>n</math> ярусов сложений с <math>j</math> операциями умножения в каждом;
 +
*4. вычисление нормы вектора длины <math>n</math> требует <math>n</math> ярусов сложений с <math>1</math> операцией умножения в каждом.
  
 
=== Входные и выходные данные алгоритма ===
 
=== Входные и выходные данные алгоритма ===
 +
'''Входные данные''': <math>A\in\mathbb{R}^{n\times n}</math> - симметричная матрица, т. е. <math>a_{ij}= a_{ji}, i, j = 1, \ldots, n</math>. Объем данных: <math>\frac{n (n + 1)}{2}</math>.
 +
 +
'''Выходные данные''': <math>\Lambda</math> - вектор собственных значений матрицы и соответствующие им собственные вектора <math>v_i,i=1,\ldots, k </math>. Объем данных: <math> k(n+1) </math>.
  
 
=== Свойства алгоритма ===
 
=== Свойства алгоритма ===
 +
* В классическом алгоритме Ланцоша возникает большая погрешность при округлении чисел с плавающей точкой. Выбранный вариант с полной переортогонализацией устраняет этот недостаток, однако является более ресурсоемким. На практике наиболее популярен вариант с частичной переортогонализацией.
 +
* Вычислительная мощность алгоритма (отношение числа операций к суммарному объему данных) оценивается как <math>\approx 2k</math>.
 +
* Преимуществом алгоритма является то, что он начинает поиск собственных значений матрицы начиная с максимального в абсолютном смысле значения.
 +
* Нет необходимости хранения исходной матрицы на каждом вычислительном ядре, так как метод использует исходную матрицу только в операциях умножения матрицы на вектор, что позволяет эффективно использовать регулярность структуры матрицы.
 +
* Существует модифицированный блочный вариант алгоритма, применяемый в случае кратных собственных значений.
 +
 +
== Программная реализация алгоритма ==
 +
  
 +
=== Особенности реализации последовательного алгоритма ===
 
=== Локальность данных и вычислений ===
 
=== Локальность данных и вычислений ===
 +
=== Возможные способы и особенности параллельной реализации алгоритма ===
 +
=== Масштабируемость алгоритма и его реализации ===
  
−
==== Локальность реализации алгоритма ====
+
Проверка масштабируемости алгоритма проходила на [//hpc.cmc.msu.ru/ IBM Blue Gene/P ВМК МГУ.]
  
−
===== Структура обращений в память и качественная оценка локальности =====
+
Используемые компиляторы: intel/15.0.090 и OpenMPI/1.8.4-icc.
  
−
===== Количественная оценка локальности =====
+
Для проведения расчетов и получения полноценной картины поведения алгоритма в зависимости от входных данных и числа процессоров, программа была запущена на следующих параметрах:
 +
* размеры входной матрицы: [5000:30000] c шагом 5000;
 +
* число процессоров: от 1, 2, 4 .. 64.
  
−
=== Возможные способы и особенности параллельной реализации алгоритма ===
+
Сборка осуществлялась с параметрами:
 +
*openmpi/1.5.5-icc
 +
*intel/13.1.0
  
−
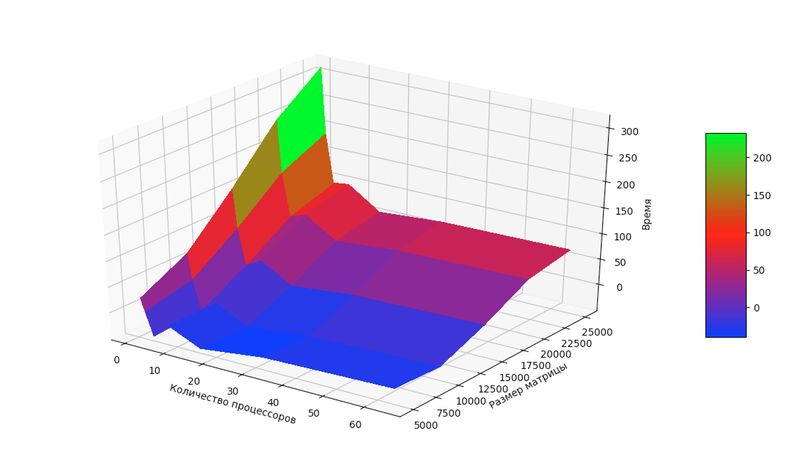
=== Масштабируемость алгоритма и его реализации ===
+
[[Файл:Lancos prof.jpg|центр|мини|800x800пкс|Рис. 2. Зависимость времени выполнения программы от входных данных]]
  
−
==== Масштабируемость алгоритма ====
+
По графику видно, что время выполнения уменьшается с увеличением количества процессоров примерно до 16, дальше начинает медленно увеличиваться вплоть до 64 и далее. Это можно объяснить тем, что с увеличением количества вычислительных ядер растет количество передаваемых данных, и дальнейшее увеличение их числа только ухудшает положение.
  
−
==== Масштабируемость реализации алгоритма ====
+
[http://pastebin.com/sWQ9ihcW код программы]
  
 
=== Динамические характеристики и эффективность реализации алгоритма ===
 
=== Динамические характеристики и эффективность реализации алгоритма ===
 +
=== Выводы для классов архитектур ===
 +
=== Существующие реализации алгоритма ===
 +
 +
The IETL Project http://www.comp-phys.org/software/ietl/ C++
 +
 +
NAG Library http://www.nag.com/content/nag-library C, C++, Fortran, C#, MATLAB, R
 +
 +
ARPACK https://people.sc.fsu.edu/~jburkardt/m_src/arpack/arpack.html MATLAB
 +
 +
GrapLab https://turi.com/products/create/open_source.html C++
  
−
=== Выводы для классов архитектур ===
+
LANSO/PLANSO http://web.cs.ucdavis.edu/~bai/ET/lanczos_methods/overview_PLANSO.html Fortran (уже распараллелена)
 +
 
 +
Julia Math  https://github.com/JuliaMath/IterativeSolvers.jl Julia
  
−
=== Существующие реализации алгоритма ===
+
SciPy https://scipy.org/ Python
  
 
== Литература ==
 
== Литература ==
 +
 +
Дж. Деммель «Вычислительная линейная алгебра» (стр. 391)
  
 
<references \>
 
<references \>
  
−
#[[en:Cholesky decomposition]]
 
−
 
−
#[[Категория:Законченные статьи]]
 
 
#[[Категория:Разложения матриц]]
 
#[[Категория:Разложения матриц]]

Текущая версия на 13:15, 4 октября 2017

Symbol wait.svgЭта работа прошла предварительную проверку
Дата последней правки страницы: 04.10.2017
Данная работа соответствует формальным критериям.
Проверено ASA.



Алгоритм Ланцоша с полной переортогонализацией
Последовательный алгоритм
Последовательная сложность [math]O(n^2k)[/math]
Объём входных данных [math]\frac{n(n + 1)}{2}[/math]
Объём выходных данных [math]k(n + 1)[/math]


Авторы: А.В.Ерошкин (ссылкаКод), М.М.Маликов (ссылка)

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Алгоритм Ланцоша - итерационный метод, используемый для вычисления части собственных значений и соответствующих им собственных векторов матрицы [math]A[/math] размера [math]n*n[/math], изначально разработанный Корнелием Ланцошем. Преимуществами использования метода является относительно небольшое потребление памяти и вычислительных ресурсов, а также наличие параметра [math]k \lt \lt n[/math], контролирующего количество итераций. Несмотря на то, что алгоритм является вычислительно эффективным, первоначально сформулированный метод был плохо применим из-за численной неустойчивости - метод хорошо работал на целочисленных значениях, однако в арифметике с плавающей точкой ошибки округления давали большую погрешность. В 1970 году Ojalvo и Newman показали, как сделать метод численно стабильным и применили его для расчета крупных инженерных сооружений, подверженных динамическим нагрузкам. Кроме того, они показали способ выбора начального приближения (с использованием ГПСЧ), а также эмпирический способ для выбора числа [math]k[/math] (примерно в полтора раза больше искомого числа собственных векторов). В данный момент существует две основных модификации метода (с полной и выборочной переортогонализацией), а также большое количество модификаций, использующихся в различных технических областях. Алгоритм используется для больших [math]n[/math].

1.2 Математическое описание алгоритма

Первый этап алгоритма - использование метода Ланцоша для построения крыловского подпространства: [math] K_k(A,x) = span[x_1, Ax_1, A^2x_1, ..., A^{k-1}x_1] [/math]. Входные данные алгоритма: квадратная симметричная матрица [math]A[/math] размерности [math]n*n[/math], вектор начального приближения [math]b[/math], а так же число итераций [math]k[/math]. Метод осуществляет поиск трехдиагональной симметричной матрицы [math]T_k=Q_k^TAQ_k[/math].

[math]T_k=\begin{bmatrix} \alpha_1 & \beta_2 \\ \beta_2 & \alpha_2 & \beta_3 &\\ &. & . & .\\ &&\beta_{k-1} & \alpha_{k-1} & \beta_k\\ &&&\beta_k & \alpha_k \end{bmatrix}[/math]

Описание метода:

[math] \begin{array}{l} q_1 = b / \Vert b \Vert_2\\ j = \overline{1, k}:\\ \quad z_j = A q_j \\ \quad \alpha_j = q_j^T z_j \\ \quad z_j = z_j - \sum_{i=1}^j (z_j^T q_i) q_i\\ \quad z_j = z_j - \sum_{i=1}^j (z_j^T q_i) q_i\\ \quad \beta_j = \Vert z_j \Vert_2\\ \quad q_{j+1} = z_j / \Vert z_j \Vert_2 = z_j/\beta_j \end{array} [/math]

Следующий шаг алгоритма - процедура Рэлея-Ритца. Она зкалючается в интерпретации собственных значений матрицы [math] T_k=Q_k^TAQ_k[/math]. Ее собственные значения приближают собственные значения исходной матрицы. Пусть Tk=V[math]\Lambda[/math]VT - спектральное разложение матрицы Tk, тогда столбцы матрицы QkV рассматриваются как приближения к соответствующим собственным векторам матрицы A и называются векторами Ритца. Числа и векторы Ритца являются оптимальными приближениями к собственным значениям и собственным векторам матрицы A.

Поиск собственных значений матрицы T намного легче, чем для исходной матрицы, так как предполагается, что [math]k \lt \lt n[/math], и матрица T - трехдиагональная.

Полная переортогонализация необходима для того, чтобы гарантировать, что каждый полученный вектор qj+1 ортогонален уже имеющимся векторам q1..j. Без этого процесса будут накапливаться существенные вычислительный ошибки.

1.3 Вычислительное ядро алгоритма

Вычислительным ядро алгоритма состоит ииз двух основных частей:

  • [math]Aq=( \sum\nolimits_{i=^n}a_{1i}q_i, \sum\nolimits_{i=2}^na_{2i}q_i, ..., \sum\nolimits_{i=1}^na_{ni}q_i)[/math] - умножение симметричной матрицы [math]A[/math] размерности [math]n*n[/math] на вектор q размерности n.
  • [math]z=z-\sum\nolimits_{i=1}^{k}(z^Tq_i)q_i.[/math] - процесс ортогонализации Грама-Шмидта.

1.4 Макроструктура алгоритма

Основные операции алгоритма:

1. Перемножение матрицы на вектор. [math]b=Ax[/math].

2. Двойная ортогонализация методом Грмма-Шмидта. [math]z=z-\sum\nolimits_{i=1}^{j-1}(z^Tq_i)q_i,[/math] [math]z=z-\alpha_jq_j-\beta_{j}q_{j-1}.[/math]

3. Вычисление обновленного базисного вектора. [math]q_{i+1} = z/ \beta[/math].

1.5 Схема реализации последовательного алгоритма

В параграфе 1.2 приводится полная схема последовательного алгоритма.

Заполняем начальные значения алгоритма (b - начальное преближение).

[math] \begin{align} & q_1=b/||b||,\\ & \beta_1=0,\\ &q_0=0, \\ \end{align} [/math]

Для всех [math]j=1..k[/math]:

  • 1. Вычисляется j-й диагональный элемент матрицы [math]T_k[/math]: [math]z=Aq_j; \alpha_j=q_j^Tz;[/math]
  • 2. Проводится полная переортогонализация Грамма-Шмидта: [math]z =z-\sum\nolimits_{i=1}^{j-1}(z^Tq_i)q_i;[/math]
  • 3. Вычисляются значения [math]\beta_{j+1}[/math] матрицы [math]T_k[/math]: [math]\beta_{j+1}=||z||;[/math]
  • 4. Если [math]\beta_{j+1}=0[/math], то алгоритм завершается;
  • 5. Сохраняем значения для следующей итерации [math]q_{j+1}=z/\beta_{j+1}.[/math]

1.6 Последовательная сложность алгоритма

  • 1. Основная часть операций в алгоритме Ланцоша производится во время умножения матрицы [math]A[/math] размерности [math]n*n[/math] на вектор [math]q[/math] размерности [math]n[/math] - вычислительная сложность: [math]n^2[/math] умножений и [math]n^2-n[/math] сложений. Остальные операции основного цикла производят меньше [math]n^2[/math] операций сложения или умножения. Так как умножение матрицы на вектор производится [math]k[/math] раз, то сложность этой части алгоритма - [math]O(kn^2)[/math]
  • 2. Процесс ортогонализации Грама-Шмидта - вычислительная сложность: [math]k^2n+k(n+2)[/math] умножений и [math]k^2n + k(n + 1) + 2[/math] сложений. Производится в цикле [math]k[/math] раз. Сложность - [math]O(nk^2)[/math]
  • 3. Процесс разложения матрицы [math]T[/math] размерности [math]k*k[/math]. Сложность - [math]O(k^2)[/math]

Так как число итераций много меньше размерности матрицы [math]A[/math], [math]k \lt \lt n[/math], то общая сложность алгоритма сокращается до [math]O(kn^2)[/math].

1.7 Информационный граф

Рис. 1. Граф j-й итерации.

Черные маленькие стрелочки - куда идут данные.

Большие стрелочки - обозначение прохода по массиву (изменение индекса)

В больших кружках преобразования (операции над данными или вычисления)

В маленьких кружках запись в переменную.

1.8 Ресурс параллелизма алгоритма

Алгоритм Ланцоша - итерационный, итерации должны выполняться в строгой последовательности, и нет возможности их параллелизовать. Внутри одной итерации алгоритма ресурсами параллелизма могут быть:

  • 1. умножение матрицы размерности [math]n * n[/math] на вектор длины [math]n[/math] требует последовательного выполнения [math]n[/math] ярусов умножений и сложений;
  • 2. вычисление [math]\alpha_j[/math] требует [math]n[/math] ярусов сложений с 1 операцией умножения в каждом;
  • 3. переортагонализация требует вычисления [math]j[/math] ярусов сложений с [math]n[/math] операциями умножения в каждом, [math]n[/math] ярусов сложений с [math]j[/math] операциями умножения в каждом;
  • 4. вычисление нормы вектора длины [math]n[/math] требует [math]n[/math] ярусов сложений с [math]1[/math] операцией умножения в каждом.

1.9 Входные и выходные данные алгоритма

Входные данные: [math]A\in\mathbb{R}^{n\times n}[/math] - симметричная матрица, т. е. [math]a_{ij}= a_{ji}, i, j = 1, \ldots, n[/math]. Объем данных: [math]\frac{n (n + 1)}{2}[/math].

Выходные данные: [math]\Lambda[/math] - вектор собственных значений матрицы и соответствующие им собственные вектора [math]v_i,i=1,\ldots, k [/math]. Объем данных: [math] k(n+1) [/math].

1.10 Свойства алгоритма

  • В классическом алгоритме Ланцоша возникает большая погрешность при округлении чисел с плавающей точкой. Выбранный вариант с полной переортогонализацией устраняет этот недостаток, однако является более ресурсоемким. На практике наиболее популярен вариант с частичной переортогонализацией.
  • Вычислительная мощность алгоритма (отношение числа операций к суммарному объему данных) оценивается как [math]\approx 2k[/math].
  • Преимуществом алгоритма является то, что он начинает поиск собственных значений матрицы начиная с максимального в абсолютном смысле значения.
  • Нет необходимости хранения исходной матрицы на каждом вычислительном ядре, так как метод использует исходную матрицу только в операциях умножения матрицы на вектор, что позволяет эффективно использовать регулярность структуры матрицы.
  • Существует модифицированный блочный вариант алгоритма, применяемый в случае кратных собственных значений.

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

2.2 Локальность данных и вычислений

2.3 Возможные способы и особенности параллельной реализации алгоритма

2.4 Масштабируемость алгоритма и его реализации

Проверка масштабируемости алгоритма проходила на IBM Blue Gene/P ВМК МГУ.

Используемые компиляторы: intel/15.0.090 и OpenMPI/1.8.4-icc.

Для проведения расчетов и получения полноценной картины поведения алгоритма в зависимости от входных данных и числа процессоров, программа была запущена на следующих параметрах:

  • размеры входной матрицы: [5000:30000] c шагом 5000;
  • число процессоров: от 1, 2, 4 .. 64.

Сборка осуществлялась с параметрами:

  • openmpi/1.5.5-icc
  • intel/13.1.0
Рис. 2. Зависимость времени выполнения программы от входных данных

По графику видно, что время выполнения уменьшается с увеличением количества процессоров примерно до 16, дальше начинает медленно увеличиваться вплоть до 64 и далее. Это можно объяснить тем, что с увеличением количества вычислительных ядер растет количество передаваемых данных, и дальнейшее увеличение их числа только ухудшает положение.

код программы

2.5 Динамические характеристики и эффективность реализации алгоритма

2.6 Выводы для классов архитектур

2.7 Существующие реализации алгоритма

The IETL Project http://www.comp-phys.org/software/ietl/ C++

NAG Library http://www.nag.com/content/nag-library C, C++, Fortran, C#, MATLAB, R

ARPACK https://people.sc.fsu.edu/~jburkardt/m_src/arpack/arpack.html MATLAB

GrapLab https://turi.com/products/create/open_source.html C++

LANSO/PLANSO http://web.cs.ucdavis.edu/~bai/ET/lanczos_methods/overview_PLANSO.html Fortran (уже распараллелена)

Julia Math https://github.com/JuliaMath/IterativeSolvers.jl Julia

SciPy https://scipy.org/ Python

3 Литература

Дж. Деммель «Вычислительная линейная алгебра» (стр. 391)

<references \>

Источник — https://algowiki-project.org/w/ru/index.php?title=Учacтник:Malikovmt/Алгоритм_Ланцоша_для_арифметики_с_плавающей_точкой_с_полной_переортогонализацией&oldid=22858