Backward substitution
| Backward substitution | |
| Sequential algorithm | |
| Serial complexity | O(n^2) |
| Input data | O(n^2) |
| Output data | n |
| Parallel algorithm | |
| Parallel form height | O(n) |
| Parallel form width | O(n) |
Primary authors of this description: A.V.Frolov.
Contents
- 1 Properties and structure of the algorithm
- 1.1 General description of the algorithm
- 1.2 Mathematical description of the algorithm
- 1.3 Computational kernel of the algorithm
- 1.4 Macro structure of the algorithm
- 1.5 Implementation scheme of the serial algorithm
- 1.6 Serial complexity of the algorithm
- 1.7 Information graph
- 1.8 Parallelization resource of the algorithm
- 1.9 Input and output data of the algorithm
- 1.10 Properties of the algorithm
- 2 Software implementation of the algorithm
- 3 References
1 Properties and structure of the algorithm
1.1 General description of the algorithm
Backward substitution is a procedure of solving a system of linear algebraic equations Ux = y, where U is an upper triangular matrix whose diagonal elements are not equal to zero. The matrix U can be a factor of another matrix A in its decomposition (or factorization) LU, where L is a lower triangular matrix. This decomposition can be obtained by many methods (for example, the Gaussian elimination method with or without pivoting, the Gaussian compact scheme, the Cholesky decomposition, etc.). Here we also should mention the QR decomposition when the matrix A is represented in the form A=QR, where Q is an orthogonal matrix and R is an upper triangular matrix. Since the matrix U is triangular, a procedure of solving a linear system with the matrix U is a modification of the general substitution method and can be written using simple formulas.
A similar procedure of solving a linear system with a lower triangular matrix is called the forward substitution (see[1]). Note that the backward substitution discussed here can be considered as a part of the backward Gaussian elimination in the Gaussian elimination method for solving linear systems.
There exists a similar method called the backward substitution with normalization. The scheme of this modification is more complex, since a number of special operations are performed to reduce the effect of round-off errors on the results. This modified method is not discussed here.
1.2 Mathematical description of the algorithm
Input data: an upper triangular matrix U whose elements are denoted by u_{ij}); a right-hand vector y whose components are denoted by y_{i}).
Output data: the solution vector x whose components are denoted by x_{i}).
The backward substitution algorithm can be represented as
- \begin{align} x_{n} & = y_{n}/u_{nn} \\ x_{i} & = \left (y_{i} - \sum_{j = i+1}^{n} u_{ij} x_{j} \right ) / u_{ii}, \quad i \in [1, n - 1]. \end{align}
There exists a block version of this algorithm; however, here we consider only its “dot” version.
1.3 Computational kernel of the algorithm
The computational kernel of the backward substitution algorithm can be composed of n-1 dot products of subrows of the matrix U with the computed part of the vector x:
- \sum_{j = i+1}^{n} u_{ij} x_{j} .
Here the dot products can be accumulated in double precision for additional accuracy. These dot products are subtracted from the components of the vector y and the results are divided by the diagonal elements of the matrix U. In some implementations, however, this approach is not used. In these implementations, the operation
- y_{i} - \sum_{j = i+1}^{n} u_{ij} x_{j}
is performed by subtracting the componentwise products as part of dot products from y_{i} instead of subtracting the entire dot product from y_{i}. Hence, the operation
- y_{i} - \sum_{j = i+1}^{n} u_{ij} x_{j}
and the division of the results by the diagonal elements of the matrix should be considered as a computational kernel instead of the dot product operations. Here the accumulation in double precision can also be used.
1.4 Macro structure of the algorithm
As is stated in description of algorithm’s kernel, the major part of the algorithm consists of computing the (n-1) sums
- y_{i} - \sum_{j = i+1}^{n} u_{ij} x_{j}
and dividing the results by the diagonal elements of the matrix. The accumulation in double precision can also be used.
1.5 Implementation scheme of the serial algorithm
The first stage of this scheme can be represented as
1. x_{n} = y_{n}/u_{nn}.
At the second stage, for all i form n-1 to 1, the following operations should be performed:
2. x_{i} = \left (y_{i} - \sum_{j = i+1}^{n} u_{ij} x_{j} \right ) / u_{ii}.
Note that the computations of the sums y_{i} - \sum_{j = i+1}^{n} u_{ij} x_{j} are performed in the accumulation mode by subtracting the products u_{ij} x_{j} from y_{i} for j from n to i + 1 with decreasing j. Other orders of summation lead to a severe degradation of parallel properties of the algorithm. As an example, we can mention a program fragment given in[2], where the backward substitution is discussed in the form of the backward Gaussian elimination performed with increasing summation index because of the restrictions imposed by old versions of Fortran.
1.6 Serial complexity of the algorithm
The following number of operations should be performed for the backward substitution in the case of solving a linear system with an upper triangular matrix of order n using a serial most fast algorithm:
- n divisions
- \frac{n^2-n}{2} additions (subtractions),
- \frac{n^2-n}{2} multiplications.
The main amount of computational work consists of multiplications and .additions (subtractions)
In the accumulation mode, the multiplication and subtraction operations should be made in double precision (or by using the corresponding function, like the DPROD function in Fortran), which increases the overall computation time of the algorithm.
Thus, the computational complexity of the backward substitution algorithm is equal to O(n^2).
1.7 Information graph
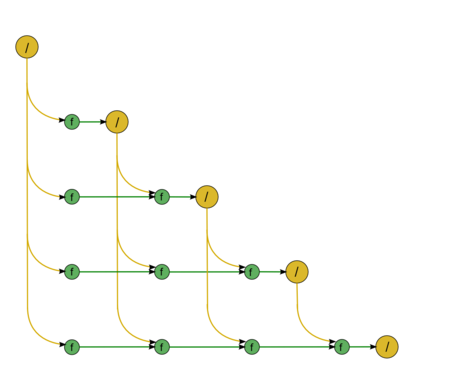
Let us describe the algorithm’s graph analytically and in the form of a figure. The graph of the backward substitution algorithm]consists of two groups of vertices positioned in the integer-valued nodes of two domains of different dimension.
The first group of vertices belongs to the one-dimensional domain corresponding to the division operation. The only coordinate i of each vertex changes in the range from n to 1 and takes all the integer values from this range.
The dividend of this division operation:
- for i = n: the input data element y_{n};
- for i \lt n: the result of the operation corresponding to the vertex of the second group with coordinates i, i+1.
The divisor of this division operation is the input data element u_{nn}.
The result of this operation is the output data element x_{i}.
The second group of vertices belongs to the two-dimensional domain corresponding to the operation a-bc.
The coordinates of this domain are as follows:
- the coordinate i changes in the range from n-1 to 1 and takes all the integer values from this range;
- the coordinate j changes in the range from n to i+1 and takes all the integer values from this range.
The arguments of this operation:
- a:
- for j = n: the input data element y_{i};
- for j \lt n: the result of the operation corresponding to the vertex of the second group with coordinates i, j+1;
- b: the input data element u_{ij};
- c: the result of the operation corresponding to the vertex of the first group with coordinate j;
The result of this operation is intermediate for the backward substitution algorithm.
The above graph is illustrated in Fig. 1 for n = 5. In this figure, the vertices of the first group are highlighted in yellow and are marked by the division sign; the vertices of the second group are highlighted in green and are marked by the letter f. The graph shows the input data transfer from the vector y, whereas the transfer of the matrix elements u_{ij} to the vertices is not shown.
1.8 Parallelization resource of the algorithm
In order to implement the backward substitution algorithm for a linear system with an upper triangular matrix of order n, a parallel version of this algorithm should perform the following layers of operations:
- n layers of divisions (one division on each of the layers),
- n - 1 layers of multiplications and n - 1 layers of addition/subtraction (on each of the layers, the number of these operations is linear and varies from 1 to n-1.
Contrary to a serial version, in a parallel version the division operations require a significant part of overall computational time. The existence of isolated divisions on some layers of the parallel form may cause other difficulties for particular parallel computing architectures. In the case of programmable logic devices (PLD), for example, the operations of multiplication and addition/subtraction can be conveyorized, which is efficient in resource saving for programmable boards, whereas the isolated division operations acquire resources of such boards and force them to be out of action for a significant period of time.
In addition, we should mention the fact that the accumulation mode requires multiplications and subtraction in double precision. In a parallel version, this means that almost all intermediate computations should be performed with data given in their double precision format. Contrary to a serial version, hence, the amount of the necessary memory increases to some extent.
Thus, the backward substitution algorithm belongs to the class of algorithms of linear complexity in the sense of the height of its parallel form; its complexity is also linear in the sense of the width of its parallel form.
1.9 Input and output data of the algorithm
Input data: an upper triangular matrix U of order n whose elements are denoted by u_{ij} and the right-hand side vector y whose components are denoted by y_{i}).
Amount of input data: :\frac{n (n + 3)}{2}; since the matrix is triangular, it is sufficient to store only the nonzero elements of the matrix U).
Output data: the solution vector x whose components are denoted by x_{i}).
Amount of output data: n.
1.10 Properties of the algorithm
In the case of unlimited computer resources, the ratio of the serial complexity to the parallel complexity is linear (the ratio of quadratic complexity to linear complexity).
The computational power of the Cholesky algorithm considered as the ratio of the number of operations to the amount of input and output data is only a constant.
The backward substitution algorithm is completely deterministic. Another order of associative operations is not considered for this algorithm’s version under study, since in this case the structure of the algorithm radically changes and the parallel complexity becomes quadratic.
The linear number of the parallel form layers consisting of a single division slows the performance of the parallel version and is a bottleneck of the algorithm, especially compared to the forward substitution, where the diagonal elements are equal to 1. In this connection, when solving linear systems, it is preferable to use the triangular decompositions for which the triangular factors contain the diagonals whose elements are equal to 1. When such triangular factors are nonsingular, it is useful, before solving the linear system, to transform them the product of a diagonal matrix and a triangular matrix whose diagonal elements are equal to 1.
There exist several block versions of the backward substitution algorithm. The graphs of some of them are almost coincident with the graph of the dot version; the distinctions consist in the ways of unrolling the loops and their rearrangements. Such an approach is useful to optimize the data exchange for particular parallel computing systems.
2 Software implementation of the algorithm
2.1 Implementation peculiarities of the serial algorithm
In its simplest version, the backward substitution algorithm can be represented in Fortran as
X(N) = Y(N) / U (N, N)
DO I = N-1, 1, -1
S = Y(I)
DO J = N, I+1, -1
S = S - DPROD(U(I,J), X(J))
END DO
X(I) = S / U(I,I)
END DO
Here S is a double precision variable if the accumulation mode is used.
2.2 Approaches and features of implementing the back substitution algorithm in parallel
There are not so many possibilities to implement the back substitution algorithm in parallel. Both of the main loops of this algorithm can be unrolled and, hence, its block version can be considered. The algorithm’s versions without unrolling the loops are possible using the completely parallel loops over I:
DO PARALLEL I = 1, N
X(I) = Y(I)
END DO
DO J = N, 1, -1
X(J) = X(J) / U(J,J)
DO PARALLEL I = 1, J-1
X(I) = X(I) - U(I,J)*X(J)
END DO
END DO
It is also possible to use the "skewed parallelism" in the above loops.
The real-valued version of the backward substitution algorithm is implemented in the basic libraries produced in Russia and in the libraries produced in western countries (for example, in LINPACK, LAPACK, ScaLAPACK, and others).
In the Russian libraries, as a rule, the accumulation mode is implemented to reduce the effect of round-off errors. In the modern western libraries, the dot versions of the algorithm are based on its LINPACK implementation utilizing the BLAS package.
In the majority of libraries, there exists a block version of the backward substitution algorithm such that its graph is topologically identical to the graph of its dot version. Since the amount of transferred data is approximately equal to the number of arithmetic operations, the optimal usage of caches in the block versions can increase their performance. Hence, an optimization of caching should first be done to optimize the performance of algorithm’s implementations.
2.3 Run results
2.4 Conclusions for different classes of computer architecture
Based on the analysis of the algorithm’s structure, we can conclude that, in order to minimize the data exchange between computing nodes, we should choose a block version such that all the matrix elements are accessible on all nodes or are distributed on the nodes in advance. In this case the amount of data transferred between the nodes is small compared to the number of arithmetic operations. In this approach, however, the largest reduction of performance efficiency is caused by the nonoptimality of computations within individual blocks. Hence, it is necessary to first optimize not an entire algorithm but the subroutines used on individual processors, such as the dot backward substitution algorithm, matrix multiplications, etc. A number of possible directions of such an optimization are discussed below.