Single-qubit transform of a state vector, scalability

1 Links

The implementation of the algorithm used for the analysis is available here.

3 Scalability of the algorithm and its implementations

3.1 Scalability of the algorithm

Because of the constant height of the parallel form the algorithm is very good scalable for the shared memory implementation. But the usage of the distributed memory leads to the locality problems.

3.2 Scalability of of the algorithm implementation

Let us perform a scalability analysis of a particular implementation of the single-qubit transform algorithm according to the scalability methodology with the use of the Lomonosov supercomputer installed at the Research Computing Center of Moscow State University.

Startup parameters:

• the number of processors [4 : 512] with the powers of 2 step;
• the number of qubits [16 : 32] with step 2.

Parallel efficiency:

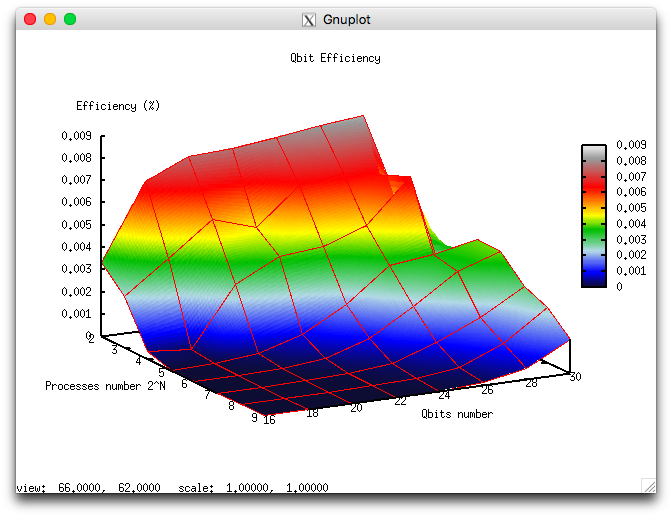
• minimum 0.000003%;
• maximum 0.008%.

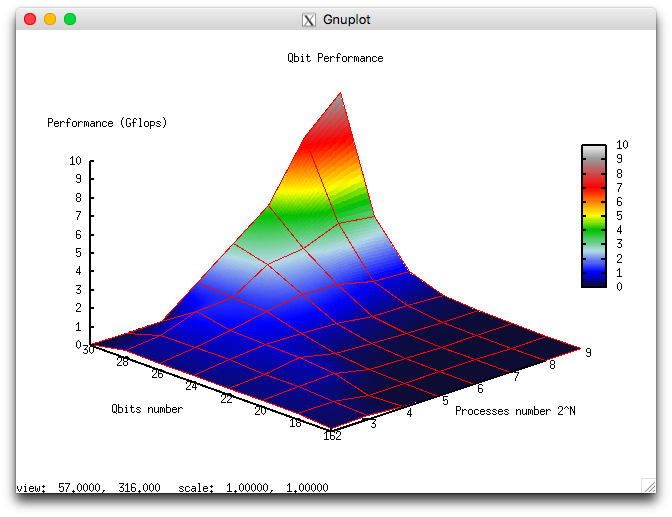
The following Figures illustrate the performance and efficiency of the chosen parallel implementation of the Cholesky algorithm, depending on the startup parameters.

Figure 1. A parallel implementation of the algorithm. Performance variation versus the number of processors and the number of qubits.

Figure 2. A parallel implementation of the algorithm. Efficiency variation versus the number of processors and the number of qubits.

for the efficiency are shown at Figure 2b. It can be seen, that efficiency is quite low, but it grows fast with the number of qubits and remains constant with simultaneous increasing of the number of processors and qubits.

4 Dynamic characteristics and efficiency of the algorithm implementation

All results were obtained on the "GraphIT!" supercomputer. For the experiments we used the Intel Xeon X5570 processors with 94 Gflops peak performance and the Gnu 4.4.7 compiler.

Figure 3. CPU Usage diagram for the single-qubit transform algorithm

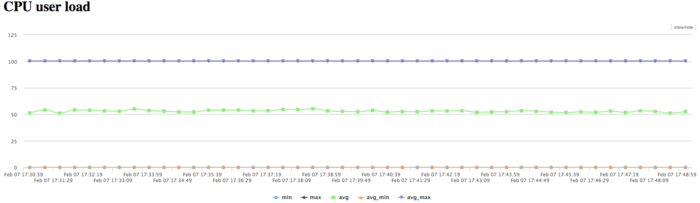
The CPU usage diagram shows that the average CPU usage during almost all the runtime of the program is about 50%. This fact shows high load, when 8 processes works on 8 processors without HyperThreading technology. It means, that the usage of all physical cores is near to 100%.

Figure 4. Diagram for the number of floating point operations per second for the single-qubit transform algorithm

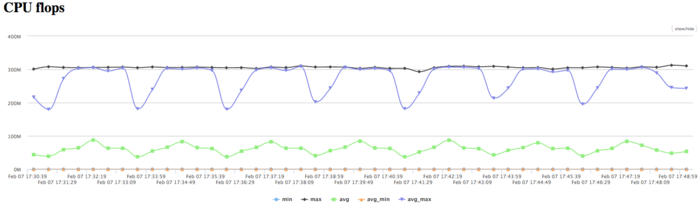
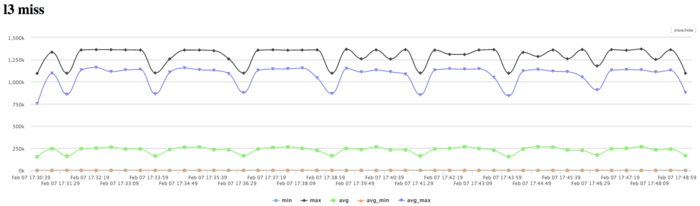
Diagram for the number of floating point operations per second shows high performane. The peak performance is 300 mln. flops, and about 70 mln. flops on average between nodes. This fact may indicate the disbalance of the computations with rather high performance.

Figure 5. Diagram for the number of L1 cache-misses per second for the single-qubit transform algorithm

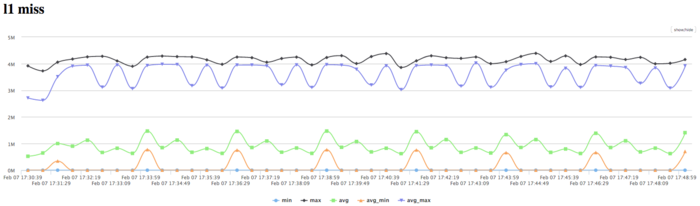
The diagram for the number of L1 cache-misses shows a high number of misses (4 mln/sec for some processe and 1 mln/sec on average). It indicates the high intensity and locality, and the disbalance of computations among processors.

Figure 6. Diagram for the number of L3 cache-misses per second for the single-qubit transform algorithm

The diagram for the number of L3 cache-misses still shows rather high number of misses (1 mln/sec at the peek and 0.25 mln/sec on average). The of L1/L3 misses is about 4 and it is average for the class of the same tasks. This value also shows low locality of computations.

Figure 7. Diagram for the number of memory read operations for the single-qubit transform algorithm

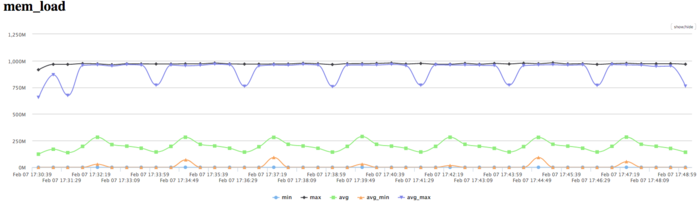
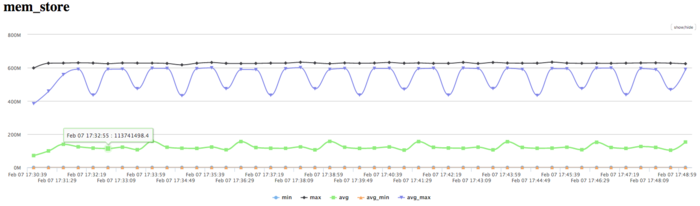
The diagram for the number of memory read operations shows low activity of memory reads. Because of the big number of working processes, the difference between peak and average value of the activity shows the computations are unbalanced. The activity is lower than for typical software of the same class.

Figure 8. Diagram for the number of memory write operations for the single-qubit transform algorithm

The activity of write operations is low, as it can be expected.

Figure 9. Plot of the number of processes ready for the execution (LoadAvg) for the single-qubit transform algorithm

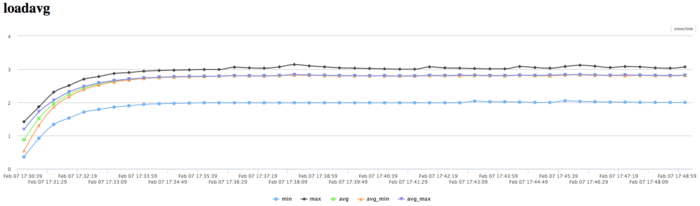
The plot of the number of processes ready for the execution (LoadAvg) shows that this value remains constant and approximately equals 3 throughout the program run. This shows that the program is operating in a stable manner, with small number of processes on each node. It confirms the suggestion about the disbalance of computations and shows that some processes have low activity.

Overall, the data obtained from the monitoring system allows one to come to the conclusion that the program under study works with low efficiency, but with the load disbalance. So, the program can be possibly optimized by the improvement of the processors balance.