Уровень алгоритма

Метод Гивенса (вращений) QR-разложения квадратной матрицы (вещественный точечный вариант)

Материал из Алговики
Перейти к навигации Перейти к поиску


Метод Гивенса (вращений) QR-разложения квадратной матрицы
Последовательный алгоритм
Последовательная сложность [math]2n^3[/math]
Объём входных данных [math]n^2[/math]
Объём выходных данных [math]n^2[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы [math]11n-16[/math]
Ширина ярусно-параллельной формы [math]O(n^2)[/math]

Основные авторы описания: А.В.Фролов.

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Метод Гивенса (в отечественной математической литературе называется также методом вращений) используется для разложения матриц в виде [math]A = QR[/math] ([math]Q[/math] - унитарная, [math]R[/math] — правая треугольная матрица)[1]. При этом матрица [math]Q[/math] хранится и используется не в явном виде, а в виде произведения матриц вращения. Каждая из матриц вращения (Гивенса)

номера столбцов: [math]\begin{matrix} \ _{i-1}\quad _i\quad _{i+1} & \ & _{j-1}\ \ _j\quad _{j+1}\end{matrix}[/math]

[math]T_{ij} = \begin{bmatrix} 1 & \cdots & 0\quad 0\quad 0 & \cdots & 0\quad 0\quad 0 & \cdots & 0 \\ \vdots & \ddots & \vdots & \vdots & \vdots & \vdots \\ 0 & \cdots & 1\quad 0\quad 0 & \cdots & 0\quad 0\quad 0 & \cdots & 0 \\ 0 & \cdots & 0\quad c\quad 0 & \cdots & 0\ -s\ 0 & \cdots & 0 \\ 0 & \cdots & 0\quad 0\quad 1 & \cdots & 0\quad 0\quad 0 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\ 0 & \cdots & 0\quad 0\quad 0 & \cdots & 1\quad 0\quad 0 & \cdots & 0 \\ 0 & \cdots & 0\quad s\quad 0 & \cdots & 0\quad c\quad 0 & \cdots & 0 \\ 0 & \cdots & 0\quad 0\quad 0 & \cdots & 0\quad 0\quad 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & \cdots & 0\quad 0\quad 0 & \cdots & 0\quad 0\quad 0 & \cdots & 1 \\ \end{bmatrix} [/math]

может быть определена парой индексов и одним параметром. Это позволяет в стандартной реализации метода Гивенса хранить результаты разложения на месте матрицы [math]A[/math] без использования дополнительных массивов. [math]QR[/math]-разложение матрицы [math]A[/math] может быть использовано в разных целях: как для решения СЛАУ вида [math]Ax = b[/math], так и в качестве одного из шагов так называемого [math]QR[/math]-алгоритма нахождения собственных чисел матрицы.

На каждом шаге алгоритма две строки преобразуемой матрицы подвергаются преобразованию вращения. При этом параметр такого преобразования подбирается так, чтобы один из поддиагональных элементов преобразуемой матрицы стал нулевым. Сначала в нуль последовательно обращаются элементы 1-го столбца, затем 2-го, и т.д. до n-1-го, после чего получившаяся матрица - это и есть матрица [math]R[/math]. Сам шаг алгоритма распадается на две части: подбор параметра вращения и выполнение вращения над двумя строками матрицы. Поскольку слева от "рабочего" столбца элементы вращаемых строк равны 0, то там выполнять вращение не нужно. Вращение элементов строк в текущем столбце выполняется одновременно с подбором параметра вращения. Таким образом, вторая часть шага заключается в выполнении вращения двумерных векторов, составленных из элементов вращаемых строк в столбцах справа от "рабочего". Каждое такое вращение эквивалентно перемножению двух комплексных чисел (или в сумме 4 умножениям, 1 сложению и 1 вычитанию действительных), одно из которых имеет модуль 1. Подбор параметра вращения по двум элементам "рабочего" столбца является более сложной операцией, что связано в том числе и с необходимостью минимизации влияния ошибок округления. Обычно для хранения матрицы вращения используется тангенс половинного угла [math]t[/math], с которым простыми формулами (т.н. "боевыми формулами тригонометрии") связаны косинус [math]c[/math] и синус [math]s[/math] самого угла:

[math]c = (1 - t^2)/(1 + t^2), s = 2t/(1 + t^2)[/math]

Именно [math]t[/math] обычно и хранится в соответствующем элементе массива.

1.2 Математическое описание алгоритма

Для получения [math]QR[/math]-разложения квадратной матрицы [math]A[/math] последнюю приводят к правой треугольной ([math]R[/math] - от слова right) последовательностью умножений её слева на матрицы вращения [math]T_{1 2}, T_{1 3}, ..., T_{1 n}, T_{2 3}, T_{2 4}, ..., T_{2 n}, ... , T_{n-2 n}, T_{n-1 n}[/math].

Каждая из матриц [math]T_{i j}[/math] задаёт вращение в 2-мерном подпространстве, связанном с [math]i[/math]-й и [math]j[/math]-й компонентами столбцов, остальные компоненты не меняются. При этом вращение подбирается так, чтобы элемент новой матрицы в [math]j[/math]-й строке и [math]i[/math]-м столбце стал нулевым. Поскольку вращения и тождественные преобразования нулевых векторов оставляют их нулевыми, то последующие вращения сохраняют полученные ранее нули слева и сверху от текущего обнуляемого элемента.

В конце процесса имеем [math]R=T_{n-1 n}T_{n-2 n}T_{n-2 n-1}...T_{1 3}T_{1 2}A[/math].

Так как матрицы вращения унитарны, то естественно получается [math]Q=(T_{n-1 n}T_{n-2 n}T_{n-2 n-1}...T_{1 3}T_{1 2})^* =T_{1 2}^* T_{1 3}^* ...T_{1 n}^* T_{2 3}^* T_{2 4}^* ...T_{2 n}^* ...T_{n-2 n}^* T_{n-1 n}^*[/math] и [math]A=QR[/math].

В вещественном случае матрицы вращения ортогональны и [math]Q=(T_{n-1 n}T_{n-2 n}T_{n-2 n-1}...T_{1 3}T_{1 2})^T =T_{1 2}^T T_{1 3}^T ...T_{1 n}^T T_{2 3}^T T_{2 4}^T ...T_{2 n}^T ...T_{n-2 n}^T T_{n-1 n}^T[/math].

Для завершения математического описания остаётся записать вычисление[2] матрицы вращения [math]T_{i j}[/math] и формулы её умножения на текущую промежуточную матрицу.

Пусть в позиции [math](i,i)[/math] преобразуемой матрицы стоит число [math]x[/math], а в позиции [math](i,j)[/math] - число [math]y[/math].

Тогда для минимизации влияния ошибок округления сначала вычисляется равномерная норма вектора [math]z = max (|x|,|y|)[/math].

Если она равна 0, то поворот не требуется: [math]t=s=0, c=1[/math].

Если [math]z=|x|[/math], то вычисляем [math]y_1=y/x[/math] и далее [math]c = \frac {1}{\sqrt{1+y_1^2}}[/math], [math]s=-c y_1[/math], [math]t=\frac {1-\sqrt{1+y_1^2}}{y_1}[/math], а в позиции [math](i,i)[/math] после поворота будет число [math]x \sqrt{1+y_1^2}[/math].

Если же [math]z=|y|[/math], то вычисляем [math]x_1=x/y[/math] и далее [math]t=x_1 - x_1^2 sign(x_1)[/math], [math]s=\frac{sign(x_1)}{\sqrt{1+x_1^2}}[/math], [math]c = s x_1[/math], а в позиции [math](i,i)[/math] после поворота будет число [math]y \sqrt{1+x_1^2} sign(x)[/math].

После получения элементов [math]c[/math] и [math]s[/math] матрицы вращения [math]T_{i j}[/math] запись преобразования для каждого столбца правее [math]i[/math]-го выглядит просто. Если в [math]k[/math]-м столбце в позиции c номером [math]i[/math] стоит x, а в позиции с номером [math]j[/math] стоит y, то их новые значения будут [math]cx - sy[/math] и [math]sx + cy[/math], соответственно, как если бы комплексное число с действительной частью [math]x[/math] и мнимой [math]y[/math] умножили на комплексное число [math](c,s)[/math].

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма можно представить состоящим из операций двух типов. Первый - операции вычисления параметров вращения, второй - вращение (может быть эквивалентно записано как произведение двух комплексных чисел, модуль одного из которых равен 1).

1.4 Макроструктура алгоритма

Операции вычисления параметров вращений образуют из себя треугольник на двумерной сетке, операции двумерных вращений - пирамиду на трёхмерной сетке.

1.5 Схема реализации последовательного алгоритма

Последовательность выполнения алгоритма обычно записывается как последовательное "обнуление" поддиагональных элементов столбцов, начиная с 1-го столбца и заканчивая предпоследним [math](n-1)[/math]-м.

При этом в рамках "обнуления" [math]i[/math]-го столбца последовательно "обнуляются" его элементы, начиная с [math](i+1)[/math]-го и заканчивая [math]n[/math]-м.

Каждое "обнуление" элемента в позиции [math](j, i)[/math] состоит из двух шагов: а) вычисление параметров матрицы вращения [math]T_{ij}[/math] таких, чтобы обнулился элемент в позиции [math](j, i)[/math]; б) умножение слева матрицы вращения [math]T_{ij}[/math] на текущую версию матрицы.

1.6 Последовательная сложность алгоритма

В последовательной версии основная сложность алгоритма определяется прежде всего массовыми операциями вращения. Они, если не учитывать возможную разреженность, составляют (в главном члене) [math]n^3/3[/math] операций комплексного умножения или, если не прибегать к ухищрениям, [math]4n^3/3[/math] вещественных умножений и [math]2n^3/3[/math] вещественных сложений/вычитаний.

При классификации по последовательной сложности, таким образом, метод Гивенса относится к алгоритмам с кубической сложностью.

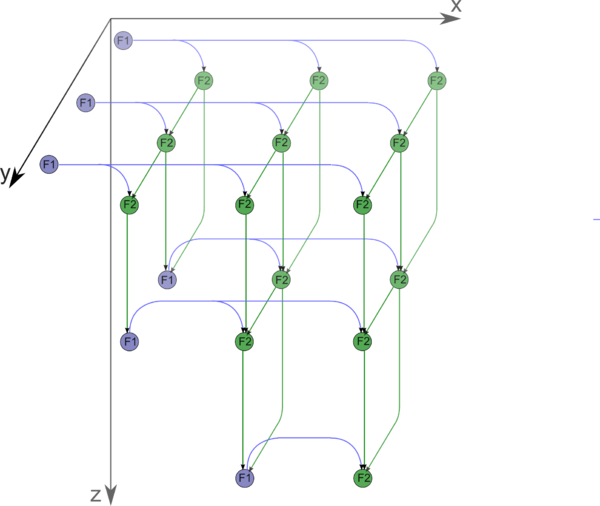
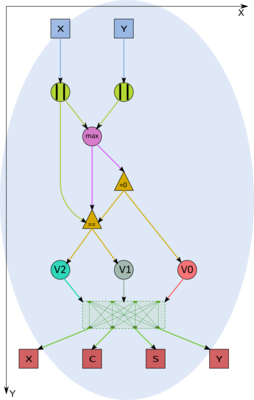
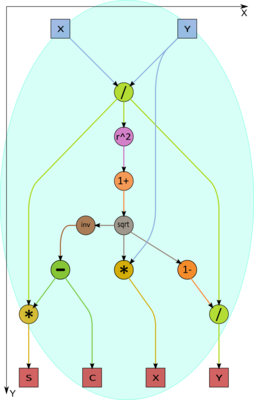
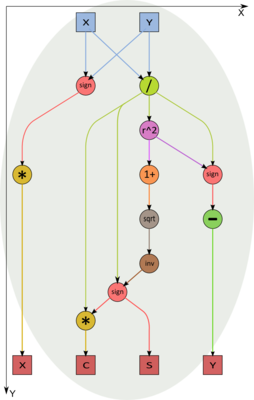
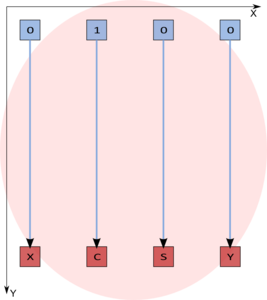
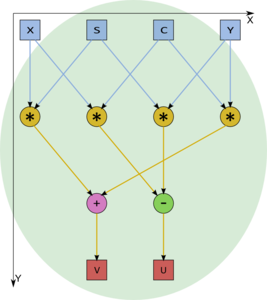
1.7 Информационный граф

Макрограф алгоритма изображён на рисунке 1, графы макровершин - на последующих.

Рисунок 1. Граф алгоритма без отображения входных и выходных данных. n=4. F1 - операция вычисления параметров поворота, F2 - выполнение поворота 2-мерного вектора (эквивалентно операции умножения двух комплексных чисел).

  • Рисунок 2. Выбор метода вычисления параметров поворота в вершинах F1.

  • Рисунок 3. Вычисление параметров поворота для различных x и y в вершине V2.

  • Рисунок 4. Вычисление параметров поворота для одинаковых x и у в вершине V1.

  • Рисунок 5. Вычисление параметров поворота для нулевых x и у в вершине V0.

  • Рисунок 6. Внутренний граф вершин F2 с входными и выходными параметрами: (u,v) = (c,s)(x,y)

1.8 Ресурс параллелизма алгоритма

Для понимания ресурса параллелизма в разложении матрицы порядка [math]n[/math] методом Гивенса нужно рассмотреть критический путь графа.

Как видно из описания подграфов, макровершина вычисления параметров поворота F1 в графе намного "весомее" вершины поворота F2. А именно, в макровершине поворота критический путь - всего-навсего одно умножение (их 4, но все можно выполнить параллельно) и одно сложение/вычитание (их 2, но они тоже параллельны). Макровершина же вычисления параметров даёт в худшем случае критический путь, в котором одно вычисление квадратного корня, и по две операции деления, умножения, сложения/вычитания.

Поэтому по грубой оценке критический путь в основном будет идти через [math]2n-3[/math] макровершины вычисления параметров F1, а также через [math]n-1[/math] макровершин поворотов. В сумме это даёт критический путь, проходящий по [math]2n-3[/math] операциям вычисления квадратного корня, [math]4n-6[/math] делениям, по [math]5n-7[/math] умножениям и сложениям/вычитаниям. В макрографе, представленном на рисунке, один из критических путей может быть представлен, например, как прохождение по "верхней линии" вершин F1 (это [math]n-1[/math] штук) и затем попеременное выполнение F2 и F1 ([math]n-2[/math] раза), после чего ещё одно выполнение F2.

Поэтому в параллельном варианте, в отличие от последовательного, вычисления квадратных корней и деления будут определять довольно значительную долю требуемого времени. При реализации на конкретных вычислительных архитектурах наличие в отдельных ярусах ЯПФ отдельных вычислений квадратных корней и делений может породить и другие проблемы. Например, при реализации на ПЛИСах остальные вычисления (умножения и сложения/вычитания) могут быть конвейеризованы, что даёт экономию и по ресурсам на программируемых платах; вычисления же квадратных корней из-за их изолированности приведут к занятию ресурсов на платах, которые будут простаивать большую часть времени.

При классификации по высоте ЯПФ, таким образом, метод Гивенса относится к алгоритмам с линейной сложностью. При классификации по ширине ЯПФ его сложность будет квадратичной.

1.9 Входные и выходные данные алгоритма

Входные данные: плотная квадратная матрица [math]A[/math] (элементы [math]a_{ij}[/math]).

Объём входных данных: [math]n^2[/math].

Выходные данные: правая треугольная матрица [math]R[/math] (ненулевые элементы [math]r_{ij}[/math] в последовательном варианте хранятся в элементах исходной матрицы [math]a_{ij}[/math]), унитарная (ортогональная) матрица Q - как произведение матриц вращения (их параметры [math]t_{ij}[/math] в последовательном варианте хранятся в элементах исходной матрицы [math]a_{ij}[/math]).

Объём выходных данных: [math]n^2[/math].

1.10 Свойства алгоритма

Соотношение последовательной и параллельной сложности, как хорошо видно, является квадратичным, что даёт хороший стимул для распараллеливания.

При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных, линейна.

Алгоритм в рамках выбранной версии полностью детерминирован.

Вычислительная погрешность в методе Гивенса (вращений) растет линейно, как и в методе отражений (Хаусхолдера).

2 Программная реализация

2.1 Особенности реализации последовательного алгоритма

В простейшем варианте метод Гивенса (вращений) QR-разложения квадратной вещественной матрицы на Фортране можно записать так: 

	DO  I = 1, N-1
		DO J = I+1, N
                    CALL PARAMS (A(I,I), A(J,I), C, S)
                    DO K = I+1, N
                       CALL ROT2D (C, S, A(I,K), A(J,K))
                    END DO
                END DO
	END DO

Подпрограмма вращения ROT2D может быть записана, если операции с комплексными числами реализованы в трансляторе грамотно, так: 

	SUBROUTINE ROT2D (C, S, X, Y)
        COMPLEX Z
        REAL ZZ(2)
        EQUIVALENCE Z, ZZ
        Z = CMPLX(C, S)*CMPLX(X,Y)
        X = ZZ(1)
        Y = ZZ(2)
        RETURN
        END

или же так: 

	SUBROUTINE ROT2D (C, S, X, Y)
        ZZ = C*X - S*Y
        Y = S*X + C*Y
        X = ZZ
        RETURN
        END

(с точки зрения графа алгоритма эти записи эквивалентны).

Подпрограмма вычисления параметров вращения может быть такой: 

	SUBROUTINE PARAMS (X, Y, C, S)
        Z = MAX (ABS(X), ABS(Y))
        IF (Z.EQ.0.) THEN
C OR (Z.LE.OMEGA) WHERE OMEGA - COMPUTER ZERO
            C = 1.
            S = 0.
        ELSE IF (Z.EQ.ABS(X))
            R = Y/X
            RR = R*R
            RR2 = SQRT(1+RR)
            X = X*RR2
            Y = (1-RR2)/R
            C = 1./RR2
            S = -C*R
        ELSE
            R = X/Y
            RR = R*R
            RR2 = SQRT (1+RR)
            X = SIGN(Y, X)*RR
            Y = R - SIGN(RR,R)
            S = SIGN(1./RR2, R) 
            C = S*R  
        END IF
        RETURN
        END

В приведенной реализации параметр матрицы вращения t записывается туда, где освобождается место (элемент преобразованной матрицы c этими индексами заведомо равен нулю), что позволяет легко восстанавливать матрицы вращения при надобности.

2.2 Возможные способы и особенности параллельной реализации алгоритма

На суперкомпьютерах кластерной (или подобной) архитектуры вполне возможна блочная нарезка алгоритма (с использованием координатных обобщённых развёрток графа алгоритма) и его распределение по разным узлам (MPI). В то же время внутренний параллелизм в блоках будет реализовывать частично многоядерные возможности узлов (OpenMP), а частично даже суперскалярность ядер. На такую реализацию следует нацелиться, исходя из структуры графа алгоритма.

Несмотря на то, что на данный момент это пока нельзя проверить на реализациях, структура графа такова, что позволяет надеяться на получение хорошей масштабируемости. За это говорит не только хороший (линейный) показатель критического пути графа, но и хорошая координатная структура обобщённых развёрток графа, что даёт возможность хорошей блочной нарезки графа алгоритма.

Поиски по известным пакетам программ привели к неожиданному результату [3]. Несмотря на то, что в большинстве старых "последовательных" пакетов как правило наличествует и программа QR-разложения методом Гивенса, в новых, рассчитанных на параллельное исполнение, пакетах QR-разложение осуществляют только с помощью метода Хаусхолдера (отражений), который именно по параллельным свойствам проигрывает методу Гивенса. Мы связываем это с тем, что метод Хаусхолдера (отражений) легко записывается через BLAS-процедуры и не требует переупорядочивания обычного хода циклов (разве что при введении блочности, но это не "косая", а координатная нарезка циклов), а вот для параллельной реализации метода Гивенса (вращений) не избежать перезаписи циклов, поскольку максимально параллельный вариант в нём требует применения cкошенного (в узком понимании этого термина) параллелизма. Поэтому временно описание масштабируемости реализаций данного алгоритма невозможно - пока нет материала для исследования этой масштабируемости.

2.3 Результаты прогонов

2.4 Выводы для классов архитектур

Сложность логической структуры модуля вычисления параметров матриц вращения позволяет нам рекомендовать читателю не использовать для работы в качестве ускорителей универсальных процессоров такие модули, как ПЛИСы, поскольку значительная часть их оборудования будет простаивать. Определённые сложности это может вызвать и на архитектуре с универсальными процессорами, однако общая структура алгоритма всё же позволяет надеяться там на хорошие показатели: так, на суперкомпьютерах кластерной архитектуры вполне возможна блочная нарезка алгоритма для распределения по разным узлам, в то время как внутренний параллелизм в блоках будет реализовывать частично многоядерные возможности узлов, а частично даже суперскалярность ядер.

3 Литература

  1. ↑ В.В.Воеводин, Ю.А.Кузнецов. Матрицы и вычисления. М.: Наука, 1984.
  2. ↑ Воеводин В.В. Вычислительные основы линейной алгебры. М.: Наука, 1977.
  3. ↑ Фролов А.В., Антонов А.С., Воеводин Вл.В., Теплов А.М. Сопоставление разных методов решения одной задачи по методике проекта Algowiki // Подана на конференцию "Параллельные вычислительные технологии (ПаВТ'2016)".
Источник — https://algowiki-project.org/w/ru/index.php?title=Метод_Гивенса_(вращений)_QR-разложения_квадратной_матрицы_(вещественный_точечный_вариант)&oldid=29087