Уровень алгоритма

Метод Хаусхолдера (отражений) для приведения симметричных матриц к трёхдиагональному виду

Материал из Алговики
Перейти к навигации Перейти к поиску


Приведение симметричной вещественной матрицы к трёхдиагональному виду методом Хаусхолдера (отражений)
Последовательный алгоритм
Последовательная сложность [math]O(n^3)[/math]
Объём входных данных [math](n^2+n)/2[/math]
Объём выходных данных [math](n^2+3n)/2[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы [math]2n^2+O(n)[/math]
Ширина ярусно-параллельной формы [math]n^2/2[/math]

Основные авторы описания: А.В.Фролов

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Метод Хаусхолдера (в советской математической литературе чаще называется методом отражений) используется для приведения симметричных вещественных матриц к трёхдиагональному виду, или, что то же самое, для разложения [math]A=QTQ^T[/math] ([math]Q[/math] - ортогональная, [math]T[/math] — симметричная трёхдиагональная матрица)[1]. При этом матрица [math]Q[/math] хранится и используется не в своём явном виде, а в виде произведения матриц отражения[2]. Каждая из матриц отражения может быть определена одним вектором. Это позволяет в классическом исполнении метода отражений хранить результаты разложения на месте матрицы A с использованием одномерного дополнительного массива.

В данной статье рассматривается именно классическое исполнение, в котором не используются приёмы типа сдваивания при вычислениях скалярных произведений.

1.2 Математическое описание алгоритма

В методе Хаусхолдера для выполнения [math]QTQ^T[/math]-разложения матрицы используются умножения слева её текущих модификаций на матрицы Хаусхолдера (отражений) с последующим умножением на те же матрицы справа.

Матрица отражений (Хаусхолдера) - матрица вида [math]U=E-2ww^*[/math], где [math]w[/math] - вектор, удовлетворяющий равенству [math]w^{*}w=1[/math]. Является одновременно унитарной ([math]U^{*}U=E[/math]) и эрмитовой ([math]U^{*}=U[/math]), поэтому обратна самой себе ([math]U^{-1}=U[/math]).

На [math]i[/math]-м шаге метода с помощью преобразования отражения "убираются" ненулевые поддиагональные элементы, начиная с [math]i+2[/math]-го в [math]i[/math]-м столбце. После умножения на эту же матрицу отражения справа автоматически убираются и ненулевые наддиагональные элементы, начиная с [math]i+2[/math]-го в [math]i[/math]-й строке, а полученная модификация снова приобретает симметричный вид.

На каждом из шагов метода матрицу отражений обычно представляют не в стандартном виде, а в виде [math]U=E-\frac{1}{\gamma}vv^*[/math], где [math]v[/math] находится через координаты текущего [math]i[/math]-го столбца так:

[math]s[/math] - вектор размерности [math]n+1-i[/math], составленный из элементов [math]i[/math]-го столбца, начиная с [math]i[/math]-го.

Если [math](s,s)=0[/math], то [math]v=e_{i}[/math], [math]\gamma = \frac{1}{2}[/math].

В остальных случаях по алгоритму вычисляется [math]u = \frac{1}{\sqrt{(s,s)}}s[/math], и далее [math]v_{j}=0[/math] при [math]j \lt i[/math], [math]v_{j}=u_{j-i+1}[/math] при [math]j \gt i[/math], а [math]v_{i}=1[/math], если [math]u_{1}=0[/math] и [math]v_{i}=\frac{u_{1}}{|u_{1}|}(1+|u_{1}|)[/math] для остальных значений. При этом [math]\gamma = 1+|u_{1}|=|v_{i}|[/math].

После вычисления вектора [math]v[/math] подстолбцы справа от ведущего модифицируются по формулам [math]x'=x-\frac{(x,v)}{\gamma}v[/math]. Потом по аналогичным формулам модифицируются строки ниже ведущей. Благодаря ассоциативности этих операций после вычисления вектора [math]v[/math] можно сразу выписать формулы модификации всех элементов справа и снизу от ведущих столбца и строки. Оказывается, что если для каждого столбца матрицы [math]x^{(j)}[/math] с номером [math]j[/math] известно [math]\beta_{j}=\frac{(x^{(j)},v)}{\gamma}[/math], то для модифицируемого элемента матрицы [math]y[/math] в позиции [math](i,j)[/math] выполняется модификация [math]y' = y - \beta_{i} v_{i} - \beta_{j} v_{j} - \Delta v_{i} v_{j}[/math], где [math]\Delta = \frac{(\beta,v)}{\gamma}[/math]. При этом все эти модификации на каждом конкретном шаге алгоритма для разных пар [math](i,j)[/math] можно выполнять независимо друг от друга, в том числе и параллельно.

1.3 Вычислительное ядро алгоритма

Рисунок 1. Граф первой половины шага алгоритма приведения к трёхдиагональному виду с отображением входных данных. Изображён граф первой половины шага с номером [math]n-4[/math]. Квадраты - результаты выполнения операций предыдущего шага. Если шаг первый, то это входные данные. Зелёные кружки - операция вида [math]a+b^2[/math], салатовые - операция вида [math]a+bc[/math]. Синий кружок - вычисление параметров матрицы отражения, светло-красные - вычисление коэффициентов [math]\beta_i[/math]для следующего полушага, жёлтые - вычисление вектора [math]v[/math].
Рисунок 2. Граф второй половины шага алгоритма приведения к трёхдиагональному виду с отображением входных данных. Изображён граф второй половины шага с номером [math]n-3[/math]. Квадраты - результаты выполнения операций предыдущего шага. Если шаг первый, то это входные данные. Синий, жёлтые и светло-красные кружки выполняются на первом полушаге (см. Рисунок 1). Голубые кружки - операции [math]a+bc[/math], зелёное - умножение, чёрные - операции [math]a+bc+de+fce[/math].

Основную часть алгоритма составляют вычисления на каждом шагу скалярных произведений [math](s,s)[/math] и [math](x,v)[/math] для всех подстолбцов [math]x[/math]справа от текущего, а также проводимые над нижним правым квадратом матрицы операции вида [math]y'=y-ab-cd-fbd[/math], с учётом симметрии матрицы.

1.4 Макроструктура алгоритма

Как уже сказано в описании ядра, основная часть - вычисления на каждом шагу скалярных произведений [math](s,s)[/math] и [math](x,v)[/math] для всех подстолбцов [math]x[/math] справа от текущего, а также массовые покомпонентные операции [math]y'=y-ab-cd-fbd[/math]. При этом, однако, строгая последовательность выполнения первых двух подшагов не обязательна, в силу связи получаемых векторов [math]s[/math] и [math]v[/math] можно одновременно с [math](s,s)[/math] вычислять и произведения [math](x,s)[/math] с последующим выражением через них коэффициентов модификации. Это позволяет почти вдвое уменьшать критический путь графа алгоритма.

1.5 Схема реализации последовательного алгоритма

Последовательность выполнения алгоритма обычно записывается как последовательное "обнуление" поддиагональных элементов столбцов, начиная с 1-го столбца и заканчивая предпоследним [math](n-1)[/math]-м.

При этом в каждом "обнуляемом" [math]i[/math]-м столбце "обнуляются" сразу все его поддиагональные элементы одновременно, с [math](i+1)[/math]-го до [math]n[/math]-го.

Каждое "обнуление" [math]i[/math]-го столбца состоит из двух шагов: а) вычисление параметров матрицы отражения [math]U_{i}[/math] такой, чтобы при умножении на неё слева "обнулились" все поддиагональные его элементы; б) одновременное умножение слева матрицы отражения [math]U_{i}[/math] и справа матрицы отражения [math]U_{i}^T[/math]на текущую версию матрицы.

1.6 Последовательная сложность алгоритма

В последовательной версии основная сложность алгоритма определяется прежде всего вычислениями скалярных произведений векторов, а также массовых модификаций элементов вида [math]y'=y-\alpha v - \beta w - \Delta vw[/math]. Они, если не учитывать возможную разреженность, составляют (в главном члене) по [math]O(n^3)[/math] операций действительного умножения и сложения/вычитания.

При классификации по последовательной сложности, таким образом, метод Хаусхолдера относится к алгоритмам с кубической сложностью.

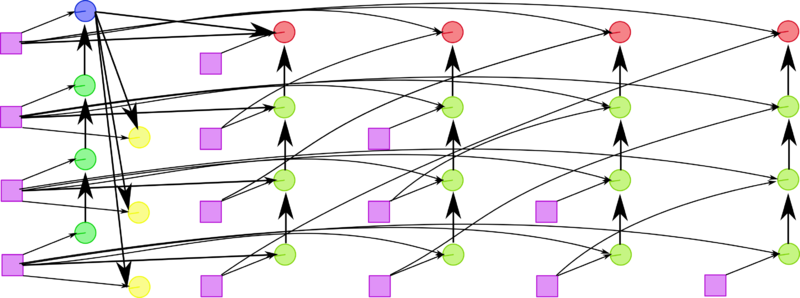
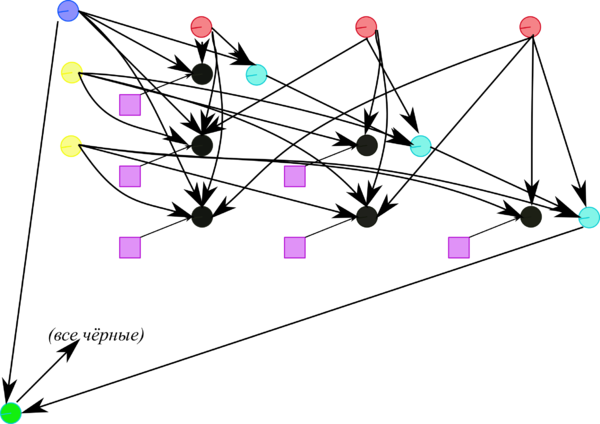
1.7 Информационный граф

На рисунках 1 и 2 приведён граф алгоритма шага метода Хаусхолдера в наиболее его быстром (с параллельной точки зрения) варианте, использующем то, что с точностью до множителя ведущий вектор матрицы отражения отличается от подстолбца, где выполняется очередное исключение, только одним элементом.

1.8 Ресурс параллелизма алгоритма

Для понимания ресурса параллелизма в симметричном приведении матрицы порядка [math]n[/math] к трёхдиагональной методом Хаусхолдера нужно рассмотреть критический путь графа.

Как видно из описания разных вершин, вычисления при "обнулении" [math]i[/math]-го столбца параметров отражения и скалярных произведений состоят из основной части - ветви длиной по [math]2(n-i)[/math] умножений и сложений - и коррекции вычислений, которые составляют [math]O(1)[/math] операций.

Поэтому по грубой (без членов низших порядков) оценке критический путь метода Хаусхолдера будет идти через [math]n^2[/math] умножений и [math]n^2[/math] сложений/вычитаний.

Поэтому в параллельном варианте, как и в последовательном, основную долю требуемого для выполнения алгоритма времени будут определять операции вида [math]a+bc[/math].

При классификации по высоте ЯПФ, таким образом, метод Хаусхолдера относится к алгоритмам с квадратичной сложностью. При классификации по ширине ЯПФ его сложность будет также квадратичной (без расширения ряда ярусов, связанных с векторными операциями сложения, пришлось бы увеличить вдвое длину критического пути).

1.9 Входные и выходные данные алгоритма

Входные данные: плотная симметричная квадратная матрица [math]A[/math] (элементы [math]a_{ij}[/math]).

Объём входных данных: [math](n^2+n)/2[/math].

Выходные данные: трёхдиагональная матрица [math]D[/math] (ненулевые элементы [math]r_{ij}[/math] в последовательном варианте хранятся в элементах исходной матрицы [math]a_{ij}[/math]), унитарная (ортогональная) матрица Q - как произведение матриц Хаусхолдера (отражения) (их вектора нормалей к плоскостям отражения в последовательном варианте хранятся в поддиагональных элементах исходной матрицы [math]a_{ij}[/math] и в одном дополнительном столбце размерности n).

Объём выходных данных: [math](n^2+3n)/2[/math].

1.10 Свойства алгоритма

Соотношение последовательной и параллельной сложности, как хорошо видно, является линейным, что даёт определённый стимул для распараллеливания. Однако у наискорейшей ЯПФ ширина квадратична, что указывает на дисбаланс между загруженностями устройств при попытке её реально запрограммировать. Поэтому более практично даже при хорошей (быстрой) вычислительной сети оставить количество устройств (например, узлов кластера) линейным по размеру матрицы, что удвоит критический путь реализуемой ЯПФ.

При этом вычислительная мощность алгоритма, как отношение числа операций к суммарному объему входных и выходных данных, линейна.

Алгоритм в рамках выбранной версии полностью детерминирован.

Вычислительная погрешность в методе отражений (Хаусхолдера) растет линейно, как и в методе Гивенса (вращений).

2 Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

В варианте с кратчайшим критическим путём графа алгоритма (с использованием зависимости между обнуляемым вектором и направляющим вектором отражения) метод Хаусхолдера (отражений) приведения квадратной симметричной вещественной матрицы к трёхдиагональному виду на Фортране 77 можно записать так: 

	DO  I = 1, N-2

            DO K = I, N
              SX(K)=A(N,I)*A(N,K)
            END DO
            DO J = N-1, I+1, -1
                 SX(I)=SX(I)+A(J,I)*A(J,I)
            END DO 
            DO K = I+1, N
              DO J = N-1, K, -1
                 SX(K)=SX(K)+A(J,I)*A(J,K)
              END DO
              DO J = K-1,I+1,-1
                 SX(K)=SX(K)+A(J,I)*A(K,J)
              END DO
            END DO

               ALPHA = SQRT (SX(I))
               IF (A(I+1,I).NE.0.) THEN
                  BETA = 1./ALPHA
                  DO J = I+2, N
                    A(J,I)=A(J,I)*BETA
                  END DO
                  SX(I) = A(I+1,I)*BETA+SIGN(1.,A(I+1,I))                     
                  A(I+1,I)=ALPHA
                  G=1./ABS(SX(I)) ! 1/gamma
                  SX2=0.
                  DO K = I+2, N
                     SX(K)=SX(K)*BETA*G+SIGN(A(K,I+1),SX(I))
                     SX2=SX(K)*A(K,I)+SX2                     
                  END DO
                  SX2=G*SX2
                  DO K = I+2, N
                     A(K,K) = A(K,K)-2*A(K,I)*SX(K)+SX2*A(K,I)**2
                     DO J = K+1, N
                       A (J,K) = A(J,K)-A(J,I)*SX(K)-A(K,I)*SX(I)+SX2*A(J,I)*A(K,I)
                     END DO
                  END DO
               ELSE
                  IF (ALPHA.NE.0.) THEN
                     BETA = 1./ALPHA
                     DO J = I+2, N
                       A(J,I)=A(J,I)*BETA
                     END DO
                     SX(I) = -1. 
                     A(I+1,I)=ALPHA
                     G=1.! 1/gamma
                     SX2=0.
                     DO K = I+2, N
                        SX(K)=SX(K)*BETA*G+SIGN(A(K,I+1),SX(I))
                        SX2=SX(K)*A(K,I)+SX2                 
                     END DO
                     SX2=G*SX2
                     DO K = I+2, N  
                        A(K,K) = A(K,K)-2*A(K,I)*SX(K)+SX2*A(K,I)**2                   
                        DO J = K+1, N
                          A (J,K) = A(J,K)-A(J,I)*SX(K)-A(K,I)*SX(I)+SX2*A(J,I)*A(K,I)
                        END DO
                     END DO
                  ELSE
                     SX(I)=1.
                  END IF
               END IF               

		
	END DO

Здесь симметричная трёхдиагональная матрица хранится в диагонали и нижней кодиагонали массива A, вектора v - в поддиагональной части массива, за исключением первых их элементов, для которых выделен массив SX.

Обычно же в последовательных версиях коэффициенты модификаций столбцов вычисляются целиком через скалярные произведения после вычислений параметров матрицы отражения. При этом схема чуть проще. Удлиняется критический путь графа, но для последовательных реализаций это неважно.

2.2 Возможные способы и особенности параллельной реализации алгоритма

Большинство пакетов от LINPACKа и LAPACKa до SCALAPACKa используют для приведения к трехдиагональному виду именно метод Хаусхолдера, правда, в различных модификациях (обычно с использованием BLAS). Существует большая подборка исследовательских работ по блочным версиям.

2.3 Результаты прогонов

2.4 Выводы для классов архитектур

В сравнении с методом Гивенса, который имеет естественное двумерное блочное разбиение на основе точечного метода, метод Хаусхолдера из-за худших характеристик локальности (наличие пучков рассылок) и меньшего количества независимых обобщённых развёрток графа не так хорош для реализаций на системах с распределённой памятью, как для систем с общей памятью. Поэтому на массово параллельных системах с распределённой памятью следует применять метод Хаусхолдера (если уж именно его нужно реализовать) не в точечной версии, а в разрабатываемых исследователями блочных вариантах. Следует отметить, что эти варианты - не блочная нарезка описанного метода, а самостоятельные методы. Особенно их применение рекомендуется в случаях с большой разрежённостью матрицы.

3 Литература

  1. ↑ В.В.Воеводин, Ю.А.Кузнецов. Матрицы и вычисления. М.: Наука, 1984.
  2. ↑ Воеводин В.В. Вычислительные основы линейной алгебры. М.: Наука, 1977.
Источник — https://algowiki-project.org/w/ru/index.php?title=Метод_Хаусхолдера_(отражений)_для_приведения_симметричных_матриц_к_трёхдиагональному_виду&oldid=29031