Участник:Илья Егоров/Алгоритм k-средних

Эта работа успешно выполнена Преподавателю: в основное пространство, в подстраницу Данное задание было проверено и зачтено. Проверено Konshin и Zhum.

Алгоритм k-средних (k-means)
Последовательный алгоритм
Последовательная сложность	[math]O(n\times k\times d)[/math]
Объём входных данных	[math]n\times d[/math]
Объём выходных данных	[math]n[/math]

Страница создана группой "Илья Егоров — Евгений Богомазов".

Оба автора в равной мере участвовали в написании, обсуждении и оформлении содержимого статьи. Допустимо считать вклад каждого равным 50%.

1 ЧАСТЬ. Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Алгоритм кластеризации k-средних впервые был предложен в 1950-х годах математиками Гуго Штейнгаузом и Стюартом Ллойдом независимо друг от друга. Наибольшую популярность он получил после работы Маккуина.

Алгоритм позволяет при заданном числе [math]k[/math] построить [math]k[/math] кластеров, расположенных на максимальном расстоянии друг от друга. Таким образом, наибольшей точности результат выполнения алгоритма достигает при полной осведомленности Пользователя о характере кластеризуемых объектов и, как следствие, при обладании максимально корректной информацией о числе кластеров.

В общем случае выбор числа [math]k[/math] может базироваться на любых значимых факторах, в том числе на результатах предшествующих исследований, теоретических соображениях или интуиции.

1.2 Математическое описание алгоритма

Исходные данные:

• Совокупность [math]n[/math] [math]d[/math]-мерных векторов [math] X = \{x_1 \dots x_n\} , [/math] где [math] x_i = \{x_{i1} \dots x_{id}\} [/math]
• Предполагаемое количество кластеров [math]k[/math]

Выходные данные:

• Разбиение X на множество [math] S = \{S_1 \dots S_k \}, \bigcup S_i = X, S_i \cap S_j = \emptyset, i \neq j [/math]
• k центров кластеров [math] \Mu = \{\mu_1 \dots \mu_k \} [/math], где [math] \mu_i = \{\mu_{i1} \dots \mu_{id} \} [/math] такие, что

[math] \begin{cases}\tilde{\mu_i} = \underset{y}{\rm argmin } \sum_{x \in S_i} ||x-y||^2_E \\ \Mu = \underset{\tilde{\Mu}}{\rm argmin } \sum_{i \in k} \sum_{x \in S_i} ||x-\tilde{\mu_i}||^2_E \end{cases} [/math]

Алгоритм:

1) [math] \mu_{i} = {\rm random} [/math]

2) [math] S_i = \{x \in S~|~\underset{j}{\rm argmin } ||x-\mu_j||_E = i\} i = 1 \dots k [/math]

3) [math] \tilde{\mu_{i}} = E_{x \in S_i}(x) [/math]

4) Если для [math] \forall i: \mu_i = \tilde{\mu_i} [/math] то алгоритм завершен, иначе [math] \mu_i = \tilde{\mu_i} [/math] и перейти на пункт 2)

1.3 Вычислительное ядро алгоритма

Вычислительным ядром алгоритма является второй этап, а точнее нахождение матрицы расстояний между [math]X[/math] и [math]\Mu[/math]. Для [math]d[/math]-мерного вектора [math]a:[/math]

[math]||a||=\sqrt{\sum_{i=1\dots d} a_i^2}[/math], поэтому заполнение одной ячейки такой матрицы потребует [math]d[/math] операций умножения, [math]d-1[/math] операций сложения и одну операция вычисления квадратного корня. Но так как эти расстояния используются только для сравнения, а sqrt является монотонно возрастающей функцией, то ее можно не вычислять. Поэтому нахождения матрицы расстояний потребует всего [math]n\times k\times d[/math] операций умножений и [math]n\times k\times (d-1)[/math] операций сложений.

1.4 Макроструктура алгоритма

В алгоритме можно выделить следующие макрооперации:

• Вычисление расстояния между векторами,
• Суммирование векторов,
• Поиск минимума в векторе,
• Сравнение векторов,
• Деление вектора на скаляр.

1) На шаге инициализации центроидов в общем случае (случайный выбор элементов) макроопераций не производится. Но так как правило определения количества кластеров [math]k[/math] неоднозначно, то для некоторых вариантов макрооперации могут понадобиться. К примеру, существует класс стратегий поиска [math]k[/math], которые базируются на определении центра масс всех объектов, и для которых будут дополнительно выполняться макрооперации "Суммирование векторов" и "Деление вектора на скаляр".

2a) При составлении матрицы расстояний [math]k \times n [/math] раз производится макрооперация "Вычисление расстояния между векторами".

2b) При нахождение вектора распределения объектов по кластерам [math]n[/math] раз производится макрооперация "Поиск минимума в векторе".

3) При пересчете центроидов [math]n - k[/math] раз производится макрооперация "Суммирование векторов" и [math]k[/math] раз — "Деление вектора на скаляр".

4) Для проверки критерия останова требуется [math]k[/math] раз произвести макрооперацию "Сравнение векторов" для сопоставления обновленных значений центроидов с уже имеющимися.

1.5 Схема реализации последовательного алгоритма

Последовательность шагов алгоритма следующая:

   1) Инициализация центроидов [math]\Mu[/math], [math] {\rm iter} = 1 [/math], задание максимального количество итераций [math]{\rm maxiter}[/math]
       
   2a) Нахождение матрицы расстояний [math]{\rm dist}:[/math]
   
       [math]{\rm dist}_{ij} = \sum_{l = 1\dots d} (x_{il}-\mu_{jl})^2[/math]
       
   2b) Нахождение вектора распределения объектов по кластерам [math]{\rm index}: [/math]
   
       [math]{\rm index}_{i} =   \underset{j}{\rm argmin }~{\rm dist}_{ij} [/math]
   
   3) Пересчет центроидов [math]\tilde{\Mu}:[/math]
   
       [math]\tilde{\mu_{ij}} = \sum_{l \in S_i} \dfrac{x_{lj}}{|S_i|} [/math], где [math]S_i = \{l~|~l \in 1\dots n, {\rm index}_l = i\}  [/math]
   
   4) Проверка критерия останова:
   
       Если [math] \exists i: \tilde{\mu_i} \neq \mu_i[/math], [math] {\rm iter} \lt  {\rm maxiter} [/math],
   
       то [math] {\rm inc}({\rm iter}), \Mu=\tilde{\Mu},[/math] GOTO 2.а.

1.6 Последовательная сложность алгоритма

   1) Сложность инициализации в общем случае зависит от применяемого метода генерации/получения случайных чисел, но ей можно пренебречь
   
   2a) Вычисление матрицы расстояний требует [math] n\times k\times d [/math] операций умножения и [math] n\times k\times (d-1) [/math] операций сложения
   
   2b) Нахождение вектора распределения требует [math] n\times (k-1) [/math] операций сравнения
   
   3) Для вычисления [math] \tilde{\Mu} [/math] требуется [math] (n - k + 1) \times d [/math] операций сложения и [math] k \times  d [/math] операций деления
   
   4) Для критерия останова требуется [math] n\times d [/math] сравнений

Итого: так как максимальное количество итераций задается в алгоритме заранее и не зависит от входных данных, то количество итераций ограничено константой. Тогда сложность алгоритма:

• [math] O(n\times k\times d)[/math] операций сложения/вычитания
• [math] O(n\times k\times d)[/math] операций умножения, [math] O(k\times d) [/math] операций деления

1.7 Информационный граф

Рассмотрим вычислительные этапы алгоритма k-means. Это распределение объектов по кластерам и перерасчет центроидов.

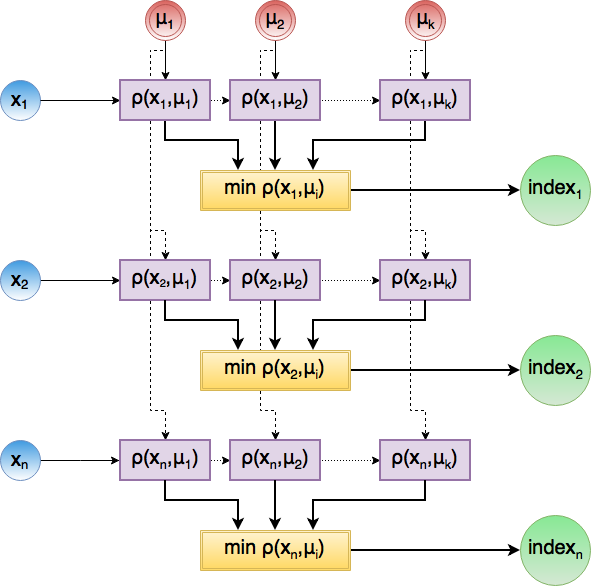
Распределение объектов по кластерам состоит из нахождения матрицы расстояний между [math]X[/math] и [math]\Mu[/math] (этапа 2a)) и нахождения индекса минимального элемента в каждой строке (этап 2b)). Ниже приведен информационный граф данного этапа.

Рисунок 1. Нахождение вектора индексов распределения по кластерам

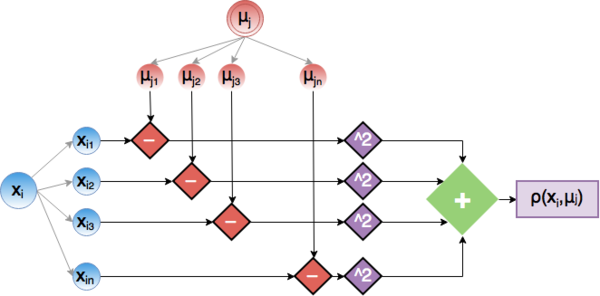
Рассмотрим этап вычисления ячейки [math] {\rm dist}_{ij} [/math] матрицы более подробно. Он представляет из себя скалярное произведение d-мерных векторов [math] x_i [/math] и [math] \mu_j [/math]. Ниже приведена граф для данной операции.

Рисунок 2. Операция вычисления расстояния

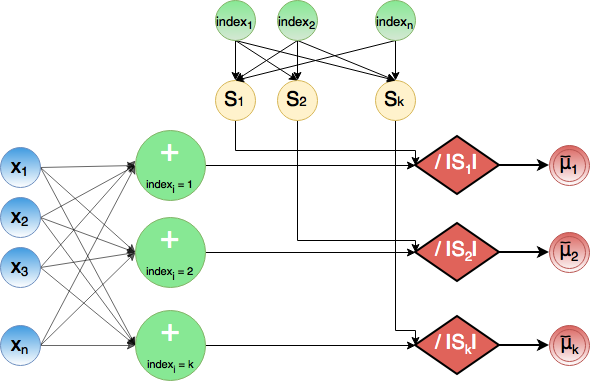
На этапе 3) происходит суммирование всех [math] x_l [/math] с одинаковым значением индекса в промежуточные суммы. Одновременно происходит подсчет количество элементов с фиксированным индексом. Затем происходит деление промежуточных сумм на соответствующее количество элементов в новом кластере, благодаря чему удается получить обновленные центроиды [math] \tilde{\mu}[/math]

Рисунок 3. Обновление центроидов

1.8 Ресурс параллелизма алгоритма

Для получения общей картины достаточно определить, в том числе и с помощью информационного графа, каким ресурсом параллелизма обладает каждый из этапов алгоритма:

2a) Нахождение каждой ячейки матрицы [math] {\rm dist} [/math] может происходить полностью независимо, так как они находятся на одном ярусе. При рассмотрении операции вычисления значения конкретной ячейки [math] {\rm dist}_{ij} [/math] можно заметить, что все операции умножения также независимы между собой, поэтому понадобится всего одно умножение. Конечный результат получается в результате суммирования всех слагаемых и достигается параллельно за [math] \log(d) [/math] бинарных операций сложения при помощи стандартного метода reduction.

2b) Нахождение вектора распределений заключается в нахождении минимального элемента в каждой строке матрицы [math] {\rm dist}[/math]. При использовании reduction эту операцию можно выполнить за [math] \log(k) [/math] бинарных операций сравнения.

3) В случае, если существует методология быстрого разделения n объектов на k множеств при помощи вектора индексации (косвенной адресации), все [math] \tilde{S_i} [/math] могут быть обработаны параллельно. В рамках каждого отдельного [math] \tilde{S_i} [/math] можно проводить распараллеливание дальше, так как [math] x_{lj} [/math] также не зависят друг от друга. Таким образом, вычисление всех слагаемых для всех [math] \tilde{\mu_{ij}} [/math] может быть выполнено за одно параллельное деление, а нахождение суммы всех этих слагаемых для каждого [math] \tilde{\mu_{ij}} [/math] может быть выполнено за [math] O(\log(n)) [/math] в худшем случае (при вхождении почти всех объектов в один кластер).

Если же такой методологии не существует, то узким местом становится процесс распределения на множества согласно вектору [math]{\rm index}[/math], который можно выполнить за [math] n [/math] операций косвенных адресаций.

4) Все сравнения для критерия останова также независимы между собой и могут быть выполнены за одну операцию сравнения, а финальный результат может быть получен за одну операцию сложения при работе над общей памятью (к примеру, прибавление единицы при несовпадении в общую память и сравнение ее с 0 по завершению) или за [math]\log(k\times d)[/math] сложений иначе.

Так как количество итераций ограничено константой, то на сложность оно не влияет. В итоге, параллельная сложность алгоритма k-means такова:

• [math] O(\log(n\times d)) [/math] операций сложения
• [math] O(\log(k)) [/math] операций сравнения
• [math] O(1) [/math] операций умножения и деления

1.9 Входные и выходные данные алгоритма

Входные данные: Количество кластеров [math]k[/math], [math]n[/math] кластеризуемых элементов

Дополнительные ограничения:

• [math]k[/math] — положительное число, т. е. [math]k \gt 0[/math].
• Для кластеризуемых элементов определена метрика (расстояние между объектами)

Объём входных данных: [math]n \times d + 1[/math] (кластеризуемые объекты в виде векторов и число [math]k[/math])

Выходные данные: Массив, в который записаны принадлежности каждого элемента кластеру (допустим вывод в другой эквивалентной более удобной структуре).

Объём выходных данных: Размер массива равен [math]2 \times n[/math].

1.10 Свойства алгоритма

Вычислительная мощность

Число действий: [math]n\cdot k\cdot d[/math] умножений

Объем входных данных: [math]n \cdot d + 1[/math]

Вычислительная мощность [math] = \dfrac{n \cdot k \cdot d}{n\cdot d + 1} = k[/math] операций на единицу переданных данных за одну итерацию.

Ограничения алгоритма

Алгоритм эффективно работает только на небольших объемах данных.

Преимущества алгоритма

• Простота использования
• Быстрота использования
• Понятность и прозрачность описания
• Обладает вычислительной устойчивостью
• Предрасположенность к распараллеливанию
• Достаточно популярный, поэтому имеет множество реализаций и вариаций

Недостатки алгоритма

• Нет проверки корректности выбора числа кластеров
• Алгоритм чувствителен к количеству кластеров
• Алгоритм чувствителен к выбору начальных элементов в качестве центроидов
• Алгоритм крайне чувствителен к выбросам по данным
• Медленная работа на больших объемах данных

2 ЧАСТЬ. Программная реализация алгоритма

2.4 Масштабируемость реализации алгоритма

Проведём исследование масштабируемости параллельной реализации алгоритма k-средних. Исследование проводилось на суперкомпьютере "Ломоносов" Суперкомпьютерного комплекса Московского университета. Параллельная реализация была написана самостоятельно на языке C, ссылка на реализацию. Так как на каждой итерации число действий на единицу данных не велико и данные должны быть собраны вместе при перерасчете центроидов, было решено для ускорения вычислений воспользоваться только OpenMP без MPI.

Код собирался под gcc c опцией -fopenmp. В очереди задача не стояла, так как код считался на одном процессоре, hyperthreading не использовался.

Набор и границы значений изменяемых параметров запуска реализации алгоритма:

• число процессоров [1 : 16] с увеличением в 2 раза;
• размер данных [100000 : 1600000] с увеличением в 2 раза.

В результате проведённых экспериментов были получены следующие данные:

• Максимальная эффективность в точке достигается при переходе от 1 потока на 4 при минимальном размере данных, она равна [math]87,5%[/math].
• Усредненная максимальная эффективность достигается при переходе с одного потока на два. Среднее время вычислений на всех рассмотренных потока снижается с 16,33 до 11.87 секунд, поэтому формально эффективность [math]= 16.33 / 11.87 / 2 \approx 68,4\%[/math]
• Минимальная эффективность в точке достигается при переходе от 1 потока на 16 при размере данных 800000, она равна [math]11,1\%[/math].
• Усредненная минимальная эффективность наблюдается при переходе с одного на максимальное рассматриваемое в эксперименте число потоков, равное 16. Время вычисления изменяется с 16,33 до 7,6 секунд, поэтому формально эффективность [math] = 16.33 / 7.6 / 16 \approx 14,9\%[/math]

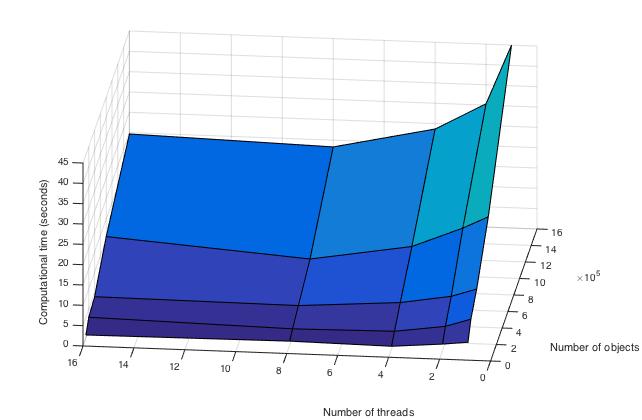
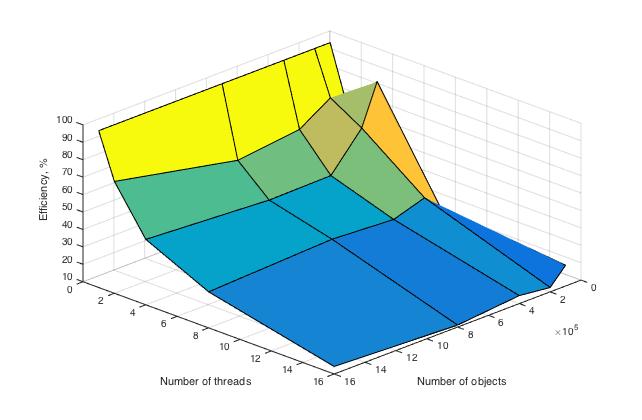
Ниже приведены графики зависимости вычислительного времени алгоритма и его эффективности от изменяемых параметров запуска — размера данных и числа процессоров:

Рисунок 4. Параллельная реализация алгоритма k-средних. Изменение вычислительного времени алгоритма в зависимости от числа процессоров и размера исходных данных.

Здесь видно, что время выполнения операций алгоритма плавно убывает по каждому из параметров, причем скорость убывания по параметру числа процессоров выше, чем в зависимоти от размера данных.

Рисунок 5. Параллельная реализация алгоритма k-средних. Изменение эффективности алгоритма в зависимости от числа процессоров и размера исходных данных.

Здесь построена эффективность перехода от последовательной реализации к параллельной. Рассчитывается она по формуле Время вычисления на 1 потоке / Время вычисления на T потоках / T, где T — это число потоков. При вычислении на 1 процессоре она равна 100 % в силу используемой формулы, что и отражено на графике.

Проведем оценки масштабируемости:

По числу процессов — при увеличении числа процессов эффективность уменьшается на всей области рассматриваемых значений, причем темп убывания замедляется с ростом числа процессов.

По размеру задачи — при увеличении размера задачи эффективность вычислений вначале кратковременно возрастает, но затем начинает относительно равномерно убывать на всей рассматриваемой области.

По размеру задачи — при увеличении размера задачи эффективность вычислений в общем случае постепенно убывает. На малых данных она выходит на пик мощности, являющийся максимумом эффективности в исследуемых условиях, но затем возвращается к процессу убывания.

2.7 Существующие реализации алгоритма

2.7.1 Бесплатный доступ

Десктопные программы

• Weka
• Orange

Фреймворки для языков

• Python:
  • scikit-learn
  • SciPy
• C++:
  • MLPACK
  • OpenCV
  • Octave
• C#:
  • Accord.NET
• Java:
  • ELKI
  • Mahout
• Lua
  • Torch

Языки R и Julia содержат алгоритм k-means в базовой реализации.

2.7.2 Платный доступ/лицензия

Существует целый перечень мощных статистических и математических пакетов для разных ОС:

• MATLAB
• Mathematica
• Stata
• SAS
• SAP HANA
• RapidMiner
• ...

3 Литература

[1] Нейский И.М. Классификация и сравнение методов кластеризации http://it-claim.ru/Persons/Neyskiy/Article2_Neiskiy.pdf

[2] https://ru.wikipedia.org/wiki/K-means