Участник:Andrclive/Уравнения мелкой воды
Основные авторы описания: А.В.Чаплыгин
Содержание
- 1 Свойства и структура алгоритмов
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритмов
1.1 Общее описание алгоритма
Уравнения мелкой воды (МВ) представляют собой упрощенную модель полных уравнений Навье-Стокса, описывающих пространственные нестационарные течения. При выводе системы уравнений МВ предполагается, что среда представляет собой достаточно тонкий слой, глубина которого много меньше его продольного размера, поэтому вертикальной составляющей скорости в слое можно пренебречь и полагать, что продольные скорости постоянны по толщине слоя.
Ситуации, когда глубина акватории много меньше горизонтальных размеров, достаточно обычна, поэтому уравнения мелкой воды находят широкое применение. Они используются с учётом кориолисовых сил при моделировании атмосферы и океана. Будем рассматривать вид задачи МВ, который используется при моделировании циркуляции океана в модели INMOM (Institute of Numerical Mathematics Ocean Model).
Уравнения мелкой воды в криволинейной системе координат при предположении [math] \zeta \lt \lt H [/math], где [math]\zeta[/math] - это отклонение уровня, а [math]H[/math] - глубина, имеют вид:
[math] \left\{ \begin{array}{ccc} \frac{\partial u}{\partial t} - lv = -\frac{1}{r_x}( \frac{1}{\rho_0}\frac{\partial p_a}{\partial x} - g\frac{\partial \zeta}{\partial x} ) \\ \\ \frac{\partial v}{\partial t} + lu = -\frac{1}{r_y}( \frac{1}{\rho_0}\frac{\partial p_a}{\partial y} - g\frac{\partial \zeta}{\partial y} ) \\ \\ \frac{\partial \zeta}{\partial t} = \frac{1}{r_x r_y} ( \frac{\partial r_y u H}{\partial x} + \frac{\partial r_x v H}{\partial y} ) \\ \end{array} \right. [/math]
[math] x, y [/math] - широта и долгота, [math] t [/math] - время, [math] u, v [/math] - зональная и меридиональная компоненты скорости, [math] l [/math] - параметр Кориолиса, [math] r_x, r_y [/math] - метрические коэффициенты, [math] p_a [/math] - атмосферное давление на поверхности, [math] g [/math] - ускорение свободного падения, [math] \rho_0 [/math] - средняя плотность жидкости.
К этой задаче также добавляются граничные условия:
[math] (\bar{U}, \bar{n}) = 0 [/math] на границе, где [math] \bar{U} = (u, v) [/math] и [math] \bar{n} [/math] - единичная нормаль к границе.
1.2 Математическое описание алгоритма
Для решения уравнений применяется техника построения разностных аппроксимаций по пространству второго порядка точности (в случае равномерной сетки) на разнесенной "C" - сетке классификации Аракавы. Уравнения требуют совместного решения сразу трех уравнений, записанных с использованием неявной схемы по времени:
[math] \left\{ \begin{array}{ccc} \frac{u^{j+1} - u^j}{\delta t} - lv^{j+1} + ru^{j+1} = -\frac{1}{r_x}( \frac{1}{\rho_0}\frac{\partial p_a}{\partial x} - g\frac{\partial \zeta}{\partial x} ) \\ \\ \frac{v^{j+1} - v^j}{\delta t} + lu^{j+1} + rv^{j+1} = -\frac{1}{r_y}( \frac{1}{\rho_0}\frac{\partial p_a}{\partial y} - g\frac{\partial \zeta}{\partial y} ) \\ \\ \frac{\zeta^{j+1} - \zeta^j}{\delta t} = \frac{1}{r_x r_y} ( \frac{\partial r_y u H}{\partial x} + \frac{\partial r_x v H}{\partial y} ) \\ \end{array} \right. [/math]
Здесь в первые два уравнения дополнительно введены слагаемые, которые можно рассматривать как рэлеевское трение с коэффициентом [math] r [/math] для дополнительного стока импульса. Они необходимы для регуляризации задачи, поскольку система может быть вырожденной.
После дискретизации системы с учетом граничных условий получаем линейную систему [math] Ax = b [/math], которую решаем итерационным методом GMRES.
1.3 Вычислительное ядро алгоритма
Формирование матрицы [math] A [/math] занимает довольно много времени и ресурсов при больших размерностях задачи, но матрица генерируется всего один раз в программе, в начале, затем на каждом шаге по времени генерируется правая часть [math] b [/math] и решается система [math] Ax = b [/math]. В процессе решения системы [math] Ax = b [/math] получается 7-диагональная плохо обусловленная матрица. Решать такую систему на каждом шаге по времени довольно затруднительно, особенно если шагов по времени довольно много, и поэтому основное время алгоритма приходится именно на этот этап.
1.4 Макроструктура алгоритма
1.5 Схема реализации последовательного алгоритма
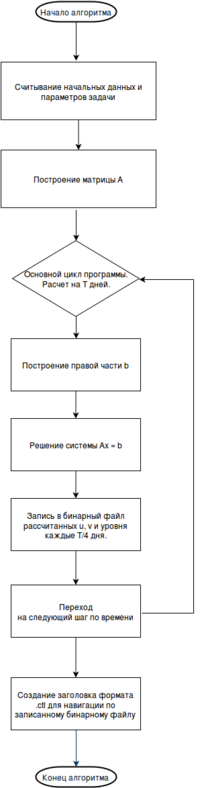
Приведем схему, показывающую структуру последовательного алгоритма.
Систему [math] Ax = b [/math] на каждом шаге по времени решаем методом GMRES с помощью PETSc.
1.6 Последовательная сложность алгоритма
При решении системы [math] Ax = b [/math] методом GMRES, необходимо провести довольно большее количество итераций - это связано со структурой матрицы [math]A[/math], о которой писалось выше. Чтобы на каждом следующем шаге по времени это число итераций уменьшить, можно в методе GMRES использовать начальное приближение не нулевое, а как решение [math]x[/math] с предыдущего шага по времени. Тогда число итераций с каждом шагом по времени будет заметно уменьшаться.
1.7 Информационный граф
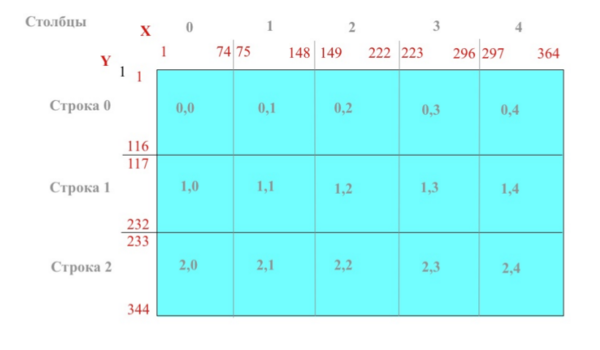
Параллельная реализация алгоритма использует метод двумерной декомпозиции области. При запуске программы из полученного числа процессоров формируется двумерная сетка, которая накладывается на рабочие массивы ([math] u, v, \zeta [/math]) во вертикале и горизонтали, в итоге каждый процессор получает свой блок из общего массива над которым он будет выполнять работу. На рисунке изображен пример разбиения массива по процессорной сетке:
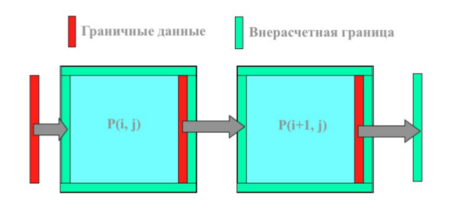
Дополнительные внерасчетные границы добавляются, чтобы производить обмен зависимыми данными между процессорами.
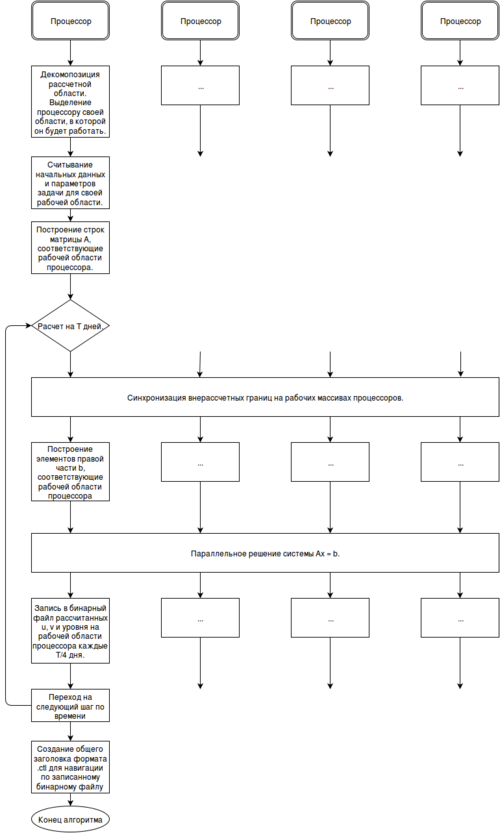
Приведем схему, показывающую структуру работы параллельной версии:
1.8 Ресурс параллелизма алгоритма
При декомпозиции области и решения системы [math] Ax = b [/math] параллельным итерационным методом, вообще говоря, число итераций может увеличиться по сравнению с последовательной версией. Для уменьшения количества итераций на каждом шаге по времени можно решать систему с использованием начального приближения не нулевого, а как решения [math]x[/math] на предыдущем шаге по времени.
1.9 Входные и выходные данные алгоритма
Входные данные алгоритма состоят из:
- Размеров и координат расчетной области.
- Топографии дна (можно просто задать глубину везде постоянной).
- Атмосферного давления на поверхности.
- Средней плотности жидкости.
- Начальных условий скоростей и уровня (обычно задаются просто нулями).
Как писалось выше, матрица [math] A [/math] - разряженная 7-диагональная плохо обусловленная матрица. Формируется и подается на вход решателю в формате CSR (Compressed Sparse Row matrix).
Выходные данные скоростей и уровня записываются в бинарный файл с последующим созданием заголовка .ctl для навигации по нему и работе с ним в программе GrADS.
1.10 Свойства алгоритма
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
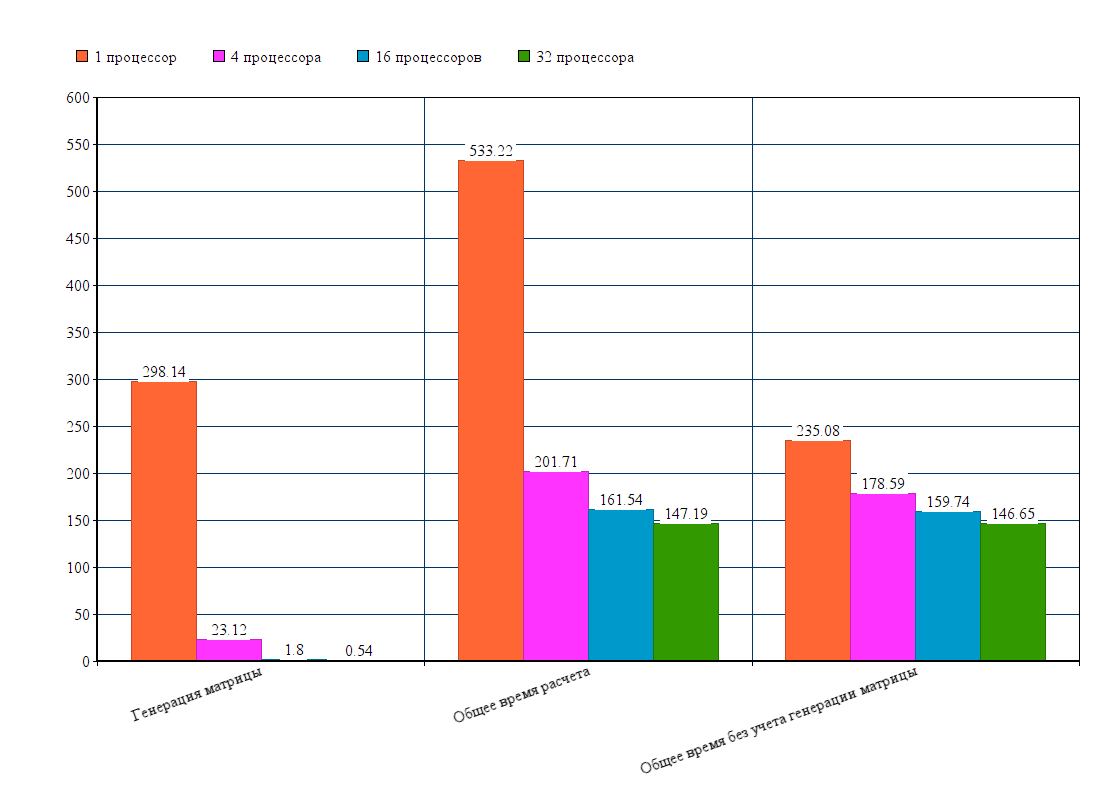
Задача рассчитывалась на сетке (1, 254)X(1, 128), на 5 дней с шагом по времени 1800 секунд (пол часа). Матрица [math] A [/math] на такой сетке имеет размеры 97920 на 97920. Все тесты проводились на суперкомпьютере Ломоносов.
Общее время расчета алгоритма:
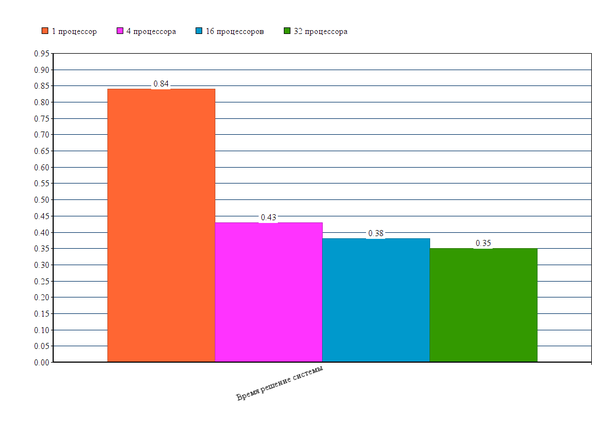
Некоторое среднее время решения системы [math] Ax = b [/math] методом GMRES с помощью пакета PETSc.
Не очень хорошая масштабируемость алгоритма связана именно с параллельным решением системы [math] Ax = b [/math]. Этот этап требует довольно большое количество пересылок между процессорами. Для достижения наилучшей производительности, сам PETSc рекомендует по 10000 неизвестных на один процессор, а лучше по 20000 ([1]).
2.5 Динамические характеристики и эффективность реализации алгоритма
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
3 Литература
- Н.А. Дианский. Моделирование циркуляции океана.
- К.М. Терехов. Параллельная реализация модели общей циркуляции океана // Сборник тезисов лучших дипломных работ 2010. ВМИК МГУ, Москва.
- PETSc [2]