Участник:SenderovichNikita/Алгоритм кластеризации, основанный на построении каркаса

Эта работа прошла предварительную проверку Дата последней правки страницы: 23.11.2016 Данная работа соответствует формальным критериям. Проверено Zhum.

MST-Кластеризация
Последовательный алгоритм
Последовательная сложность	[math]O(N^2\log N)[/math]
Объём входных данных	[math]O(N)[/math]
Объём выходных данных	[math]O(N)[/math]
Параллельный алгоритм
Высота ярусно-параллельной формы	[math]O(\log^2 N)[/math]
Ширина ярусно-параллельной формы	[math]O(N^2)[/math]

Автор статьи: Сендерович Никита Леонидович

Данный документ содержит описание алгоритма кластеризации, основанного на построении минимального остовного дерева (каркаса, остова, кратчайшего незамкнутого пути, минимального покрывающего дерева, англ. Minimum Spanning Tree (MST)) - эвристического графового алгоритма построения разбиения множества объектов на такие непересекающиеся подмножества объектов, что объекты, принадлежащие одному подмножеству, схожи по заданной метрике в большей степени, чем объекты, принадлежащие разным группам.

Как и все алгоритмы кластеризации, данный алгоритм может быть применён для решения задач кластерного анализа, выделения типовых и нетипичных объектов в рассматриваемой выборке объектов. Его достоинствами по сравнению с другими аналогичными алгоритмами машинного обучения являются наглядность, идейная простота, возможность контролировать число кластеров. Главным недостатком является ограниченная применимость: алгоритм лучше всего подходит для выделения кластеров типа сгущений или лент, наличие разреженного фона или узких перемычек между кластерами может приводить к неадекватному с точки зрения аналитика результату. Другим недостатком является высокая вычислительная сложность: на выборках более 100 тыс. объектов без применения параллельных вычислений применить алгоритм невозможно. Рассмотрению соответствующих параллельных алгоритмов и посвящена данная статья.

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Рассматривается выборка [math]X = \{x_i\}, i = 1, 2, \ldots, N[/math], состоящая из [math]N[/math] объектов с заданной симметричной неотрицательной функцией расстояния [math]\rho[/math]. Данную выборку можно рассматривать как связный неориентированный взвешенный граф [math]G[/math], множество вершин которого совпадает со множеством объектов выборки, веса рёбер соответствуют значениям функции расстояния между соответствующими вершинами.

Также должно быть задано искомое число кластеров [math]K[/math].

Рис.1. Ключевая идея алгоритма кластеризации на основе построения остовного дерева, разбиение на 3 кластера

Идея рассматриваемого алгоритма кластеризации очень проста:

• с помощью какого-либо алгоритма на определённом выше графе строится минимальное остовное дерево
• из полученного дерева выбрасывается [math]K - 1[/math] ребро с наибольшими весами, что приводит к появлению в остовном дереве [math]K[/math] компонент связности, каждая из которых объявляется кластером

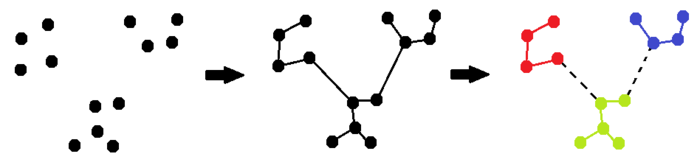
Иллюстрация работы алгоритма приведена на рис. 1. В данном случае рассматриваются 13 объектов на евклидовой плоскости, построено остовное дерево, после чего из него выброшены 2 наиболее длинных ребра и получены три кластера.

Существуют различные модификации описанного алгоритма, связанные с другим алгоритмом конструирования исходного графа или условием выбрасывания рёбер из построенного остовного дерева. Например, число [math]K[/math] может быть полезно определить не изначально, а подобрать, рассматривая отсортированную по убыванию последовательность весов рёбер в остовном дереве: если имеется резкое уменьшение весов, то можно удалить все рёбра до него. Формализацией такого подхода является алгоритм ZEMST. Однако в дальнейшем ограничимся анализом определённого выше простейшего варианта.

1.2 Математическое описание алгоритма

Пусть задан связный неориентированный граф на множестве объектов [math]G = (X, E)[/math] с неотрицательными весами рёбер [math]\rho(e) = \rho(x_i, x_j) \geqslant 0[/math].

Наиболее частый используемый на практике сценарий следующий:

• каждый объект описывается [math]d[/math]-мерным вектором в пространстве
• используется функция расстояния [math]\ell_p[/math]

Например, случай, когда в качестве метрики выбирается евклидова метрика [math]\ell_2[/math] в литературе называется EMST - Euclidean Minimum Spanning Tree.

Хотя в некоторых задачах возможна ситуация, когда данный граф не является полным (по каким-то причинам определены не все расстояния между вершинами), но в описанных типовых случаях граф является полным, содержит [math]\frac{N(N - 1)}{2} = O(N^2)[/math] рёбер.

1.2.1 Обзор алгоритмов поиска минимального остова

Для поиска минимального остовного дерева на практике используется следующие три похожих друг на друга алгоритма и их комбинации: Алгоритм Прима, Алгоритм Крускала и Алгоритм Борувки.

Кратко опишем принцип работы каждого из этих трёх широко используемых алгоритмов поиска минимального остова в предположении работы с полным графом. Все они основаны на стратегии жадного добавления рёбер в остов. Все они предполагают, что изначально множество рёбер в искомом остовном дереве пусто и отличаются тактикой добавления рёбер.

В алгоритме Прима рассматривается текущее остовное дерево [math]T[/math]. Изначально [math]T[/math] состоит из одной вершины, выбранной произвольно. Далее на каждом шаге отыскивается минимальное ребро, ровно один из концов которого принадлежит [math]T[/math], оно добавляется в [math]T[/math] вместе со вторым своим концом. Алгоритм завершается через [math]N - 1[/math] шаг - ровно столько рёбер в дереве на [math]N[/math] вершинах. Последовательная реализация, при которой минимальное ребро на каждом шаге ищется полным перебором рёбер, исходящих из [math]T[/math], имеет сложность [math]O(N^3)[/math] на полном графе. Алгоритм можно ускорить, если поддерживать двоичное дерево поиска по рёбрам, ровно один из концов которых принадлежит [math]T[/math]. Тогда при добавлении очередной вершины в [math]T[/math] необходимо добавить в двоичное дерево не более чем [math]N - 1[/math] новое ребро за [math]O(N \log N)[/math], а выбор минимума осуществляется за [math]O(\log N)[/math]. Поскольку шаг добавления вершины повторяется [math]N[/math] раз, итоговая сложность [math]O(N^2 \log N)[/math].

В алгоритме Крускала остов [math]T[/math] изначально пуст, и в остов на каждом шаге добавляется вместе со своими концами минимальное ребро, имеющееся в графе, не нарушающее свойства ацикличности уже выбранного на предыдущих шагах леса [math]T[/math]. Через [math]N - 1[/math] шаг лес [math]T[/math] гарантированно станет связным деревом. Если искать минимум полным перебором по [math]O(N^2)[/math] рёбрам полного графа, сложность получится [math]O(N^3)[/math]. Если же предварительно отсортировать все рёбра по весу за [math]O(N^2 \log N^2) = O(N^2 \log N)[/math], то дальше все рёбра искомого остова можно будет добавить в процессе одного прохода по этому массиву рёбер в порядке возрастания весов - для каждого ребра проверяем, не нарушает ли оно свойство ацикличности [math]T[/math] и добавляем его в [math]T[/math], если не нарушает. Для того чтобы быстро проверять свойство принадлежности обоих концов ребра одной из компонент [math]T[/math], используется эффективная структура данных - система непересекающихся множеств. Сложность одной такой проверки [math]O(\alpha(N))[/math], где [math]\alpha(N)[/math] - обратная функция Аккермана, значение которой не превосходит 4 для [math]N \leqslant 10^{500}[/math]. Итоговая сложность такого алгоритма равна сложности сортировки и также составляет [math]O(N^2 \log N)[/math].

В алгориме Борувки, как и в алгоритме Крускала, поддерживается лес [math]T[/math]. Изначально лес состоит из [math]N[/math] изолированных вершин графа. На каждом шаге путём перебора всех рёбер графа для каждого дерева в [math]T[/math] ищется минимальное ребро, ровно один конец которого принадлежит этому дереву. После этого все найденные рёбра добавляются в [math]T[/math]. Поскольку после каждой итерации число деревьев в лесе [math]T[/math], исходно равное [math]N[/math], уменьшается не менее чем в 2 раза, таких шагов будет произведено не более [math]\log N[/math], поэтому итоговая сложность алгоритма составляет [math]O(N^2\log N)[/math].

1.2.2 Анализ ресурса параллелизма алгоритмов поиска минимального остова

Итак, каждый из данных алгоритмов имеет сложность [math]O(N^2\log N)[/math], однако с точки зрения параллельной реализации они различаются. Эффективные реализации алгоритмов Прима и Крускала используют структуры данных, рассчитанные на последовательный характер алгоритма. Так, двоичное дерево поиска, содержащее все рёбра, исходящие из построенного на данный момент остова [math]T[/math], трудно приспособить к распределённым архитектурам. А при работе с полным графом с большим числом вершин хранить его становится практически невозможно. В алгоритме Крускала можно распараллелить этап сортировки рёбер, но на последнем шаге алгоритма необходимо последовательно просмотреть отсортированный массив [math]O(N^2)[/math] рёбер, поддерживая СНМ, что сводит на нет параллелизм. Таким образом, для этих двух алгоритмов необходима существенная переработка для получения эффективного параллельного решения .

На этом фоне выгодно выделяется исторически первый алгоритм Борувки. Он был разработан чешским учёным Отакаром Борувкой в 1926 году для решения задачи построения оптимальной электрической сети в Моравии. Он эффективнее всего использует тат факт, что остовные деревья сперва можно найти для отдельных частей графа, после чего объединить полученные деревья. Далее будем рассматривать именно этот метод для построения минимального остовного дерева в алгоритме кластеризации.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро всех алгоритмов поиска каркаса - нахождение минимального из рёбер, не приводящего к возникновению ацикличности графа. Именно для оптимизации этой операции используются эффективные структуры данных и алгоритмы. В дальнейшем будет показано, что для выбранного алгоритма Борувки на этом этапе возможна эффективная параллельная реализация. В случае использования этого алгоритма для поиска минимального остовного дерева вычисление ядра состоит в нахождении для каждого дерева из уже имеющегося остовного леса минимального исходящего из него ребра, т.е. минимального ребра, исходящего из вершин данного дерева вовне.

1.4 Макроструктура алгоритма

Основными элементами алгоритма, которые дальше будут использоваться, являются следующие процедуры:

• вычисление расстояния [math]\rho(x_i, x_j)[/math] между объектами (вершинами полного графа)
• функции для работы с графом - инициализация добавление, удаление ребра
• обход в глубину для выделения компонент связности графа: обход леса производится за [math]O(N)[/math] с помощью функции обновить_компоненты, которая возвращает массив компонента, содержащий номер компоненты связности для каждой вершины
• процедура сравнения рёбер: рёбра сравниваются по весу, а при равенстве весов - по идентификатору ребра. Это важная составная часть алгоритма Борувки, поскольку иначе на этапе добавления рёбер могут возникнуть циклы. Простейшим примером является граф из трёх вершин, все попарные расстояния между которыми равны 1: если по ходу работы для первой окажется ближайшей вторая, для второй третья, а для третьей первая, то в граф будет добавлен цикл.
• сортировка массива рёбер по их весу

1.5 Схема реализации последовательного алгоритма

Определим с помощью псевдокода ряд функций, необходимых для построения искомого результата.

Алгоритм Борувки поиска минимального остовного дерева в полном графе

 1 Вход: Выборка объектов X размера N
 2 Выход: рёбра минимального остовного дерева T
 3 Алгоритм:
 4   T := пустое множество рёбер
 5   компонента := обновить_компоненты(T)
 6   есть_разные_компоненты := 1
 7   Пока (есть_разные_компоненты равно 1):
 8     есть_разные_компоненты = 0
 9     инициализировать массив D кратчайших рёбер, исходящих из компонент, бесконечно длинными рёбрами
10     цикл по всем парам вершин (x, y) из X:
11       если компонента(x) не равно компонента(y):
12         есть разные компоненты := 1
13         d := расстояние(x, y)
14         если (ребро (x, y) < ребро D(компонента(x))):
15             D(компонента(x)) := (x, y)
16         если (ребро (x, y) < ребро D(компонента(y))):
17             D(компонента(y)) := (x, y)
18     цикл по рёбрам E из D:
19        добавить E в множество T
20     компонента := обновить_компоненты(T)
21   вернуть Т

Итоговый алгоритм кластеризации:

1 Вход: Выборка объектов X, число кластеров K
2 Выход: метки кластеров для каждого объекта из X
3 Алгоритм:
4    T := рёбра минимального остовного дерева для набора объектов X
5    E := отсортировать рёбра T по убыванию
6    цикл по первым K рёбрам в E:
7       удалить ребро из T
8    компонента := обновить_компоненты(T)
9    вернуть компонента

1.6 Последовательная сложность алгоритма

В разделе "Обзор алгоритмов поиска минимального остова" уже было показано, что алгоритм Борувки поиска остова имеет сложность [math]O(N^2 \log N)[/math]: поскольку на каждом шаге число компонент уменьшается не менее чем в 2 раза, цикл while выполнится не более [math]\log N[/math] раз. Внутри цикла находятся:

• инициализация массива [math]D[/math] кратчайших рёбер, исходящих из компонент связности, бесконечностями - [math]O(N)[/math]
• перебор по всем рёбрам полного графа и обновление содержимого ячеек массива [math]D[/math] - [math]O(N^2)[/math]
• добавление найденных рёбер из массива [math]D[/math] в граф [math]T[/math] - [math]O(N)[/math]
• обновление компонент связности в графе [math]T[/math] - [math]O(N)[/math]

После поиска остова рёбра остовного дерева сортируются за [math]O(N \log N)[/math] операций, за [math]O(N)[/math] производится выбрасывание рёбер, за [math]O(N)[/math] определяются финальные метки кластеров.

Итоговая сложность [math]O(N^2 \log N)[/math] операций. В ходе работы основными являются операции сравнения и обращения в память. Обратим внимание, что "узким местом" алгоритма является перебор по всем рёбрам для нахождения минимальных рёбер, исходящих из каждой компоненты связности остовного леса [math]T[/math].

1.7 Информационный граф

Приведём информационный граф, оставив за скобками детали реализации последних шагов алгоритма - сортировки и выбрасывания рёбер:

Рис.2. Информационная структура алгоритма кластеризации, основанного на поиске минимального остовного дерева

Кратко опишем шаги схемы. Для вычисления массива [math]D[/math] необходимо обработать некоторые из перебираемых рёбер (конкретные связи зависят от структуры текущего остовного дерева [math]T[/math]), поэтому на этом этапе присутствует нерегулярность по данным; кроме того необходима инициализация массива [math]D[/math]. Поскольку на шаге 2 для каждой компоненты необходимо выбирать минимум из набора рёбер, размер которого не ограничен константой, данная операция взятия минимума имеет, вообще говоря, параллельную сложность не менее чем [math]O(\log N)[/math]. Операции обновления структуры остовного графа независимы, могут быть распараллелены и склеены в шаг 3. Алгоритмы сортировки и поиска компонент связности теоретически имеют высоту ярусно-параллельной формы [math]O(\log N)[/math]. Независимо могут быть выполнены и последние этапы алгоритма, связанные с выбрасыванием рёбер и получением финального ответа, хотя на практике это не так уж важно. Таким образом, поскольку последовательно делается [math]O(\log N)[/math] итераций цикла, на каждой из которых высота ярусно параллельной формы имеет порядок [math]O(\log N)[/math], итоговая высота ярусно-параллельной формы (и, соответственно, параллельная сложность алгоритма) - [math]O(\log^2 N)[/math]. Ширина ярусно-параллельной формы алгоритма - [math]O(N^2)[/math].

Здесь необходимо отметить, что описанный алгоритм для поиска остовного дерева теоретически не является наиболее оптимальным: в статье приводится алгоритм для графа [math]G = (V, E)[/math], имеющий оптимальную параллельную сложность [math]O(\log N)[/math]. Однако, будучи оптимальным в теории, данный алгоритм не практичен - он исходит из числа процессоров порядка [math]O(V + E)[/math] ([math]O(N^2)[/math] в нашем случае полного графа).

1.8 Ресурс параллелизма алгоритма

Как показал анализ сложности узким местом является нахождение минимальных рёбер, исходящих из каждой компоненты связности остовного леса [math]T[/math]. Информационный граф говорит о том, что этот этап можно эффективно распаралелить, так как выбор минимального исходящего ребра для каждой компоненты связности остовного дерева и даже для каждой вершины может исполняться независимо. Процедуры инициализации массива [math]D[/math], добавления найденных рёбер в граф могут быть произведены независимо по элементам. Параллельно может быть проведена и сортировка, и выбрасывание рёбер в конце, хотя это не так принципиально в реальности. Но это позволяет оценить высоту ярусно-параллельной формы и теоретическую параллельную сложность алгоритма.

Операции на ключевом этапе алгоритма достаточно сбалансированы - в полном графе для каждой из вершин необходимо просмотреть всех её соседей, поэтому в случае равномерного по вершинам графа распределения работ, эффективность параллельной реализации будет высокой. В целом, имеет место массовый параллелизм на итерациях вычисления ближайших вершин для текущего набора компонент связности [math]T[/math].

1.9 Входные и выходные данные алгоритма

Входными данными алгоритма является описание выборки из [math]N[/math] объектов. В типовом случае каждый из них описывается [math]d[/math] координатами, однако может описываться каким-то иным способом, позволяющим находить расстояния между объектами. Также на вход передаётся число искомых кластеров [math]K[/math].

Выходом является массив из [math]N[/math] целых чисел от 1 до [math]K[/math] - номера кластеров, найденных алгоритмом кластеризации.

1.10 Свойства алгоритма

Известно, что минимальное остовное дерево определено однозначно, если в графе все рёбра различны. Очень важно ввести операцию сравнения рёбер и добиться, чтобы все рёбра были различны. Пример, когда алгоритм Борувки зацикливается из-за этого, приведён выше.

Распараллеливание описанного алгоритма может принести значительный выигрыш - без него алгоритм фактически невозможно запустить на данных с числом объектов более 100 тысяч. Теоретические возможности распараллеливания на самом сложном этапе - вычислении минимального остовного дерева - были подробно обсуждены выше. Однако на практике может возникнуть ряд трудностей, связанных с эффективным обменом информацией между процессами. Так, всем параллельно работающим процессам необходимо быстро отвечать на вопрос о расположении вершин графа в одной компоненте связности - решения этой проблемы можно добиться, если синхронизировать информацию о найденных оптимальных рёбрах в конце каждой итерации.

Кроме того, важно помнить, что в условиях полного графа каждому узлу необходима и информация обо всех кластеризуемых объектах - чтобы можно было вычислять расстояния между вершинами, не храня все [math]O(N^2)[/math] расстояний.

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

2.4.2 Масштабируемость реализации алгоритма

С помощью технологии OpenMP был реализован параллельный алгоритм построения остовного дерева, основанный на алгоритме Борувки. Был распараллелен основной bottleneck алгоритма - поиск минимального ребра, исходящего из кластеров. В качестве данных для экспериментов использовались сгенерированные случайным образом точки на плоскости.

Эксперимент производился на 16-процессорной машине под управлением операционной системы Linux, характеристики процессора: 2,6GHz Intel E3-12xx (Sandy Bridge), 8 instruction per cycle. Опираясь на эти характеристики, получаем, что пиковая теоретическая производительность одного процессора составляет 20,8 Gflops, а вычислительной системы в целом составляет 332,8 GFlops.

Вычислительная сложность каждой задачи оценивалась сверху по формуле: [math]7N^2\log N[/math], где константу 7 определяет число операций с плавающей точкой, необходимое для вычисления квадрата расстояния между двумя точками на плоскости (для выбора минимального ребра в алгоритме Борувки достаточно знать квадрат его длины).

Перебирались следующие параметры запуска, от которых самым существенным образом зависит время работы программы:

• число процессоров: от 2 до 16 с шагом 2
• число кластеризуемых объектов (точек): от 50 тысяч до 150 тысяч с шагом 10 тысяч

Для получения наиболее устойчивых результатов каждый эксперимент производился 5 раз, после чего время работы усреднялось по запускам.

Ссылка на код реализованного алгоритма и лог эксперимента: https://drive.google.com/open?id=0B4KJzu2I13loaldSbF9XUnJXQ00

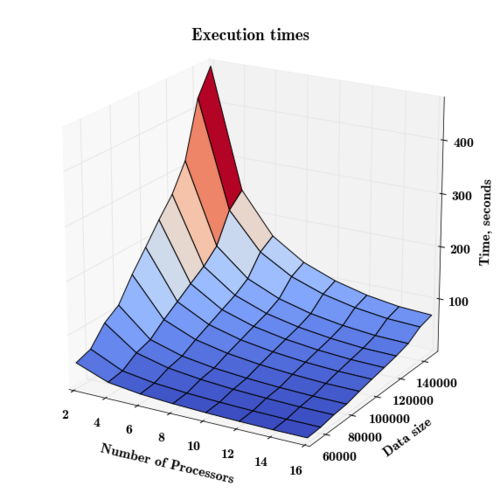
Приведём графики времени работы, производительности и эффективности в зависимости от параметров, демонстрирующие свойства параллельной реализации:

Рис.3. График времени работы программы в зависимости от числа процессов и размера задачи

Видим, что использование параллелизма позволяет существенно сократить временные затраты, однако в связи с необходимостью синхронизации процессов при переходе к очередной итерации алгоритма эффект параллелизма падает с увеличением числа процессоров. К примеру, на самой большой рассматриваемой задаче (150 тыс. точек) по сравнению с использованием 2 процессоров при использовании 4 процессоров время работы снижается примерно в 1.95 раз (с 469 до 240 секунд), а при использовании всех 16 процессоров - только в 6.8 раз вместо идеальных 8 (с 469 до 69 секунд).

Рис.4. График производительности программы в зависимости от числа процессов и размера задачи

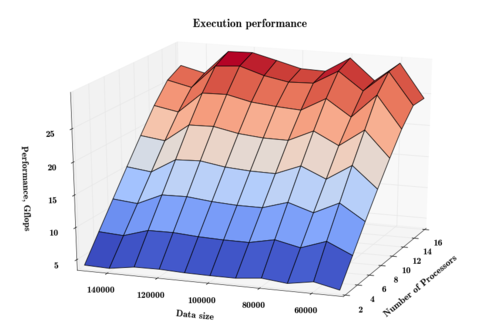
Производительность по числу процессоров напоминает линейную функцию, но при переходе от числа процессоров 14 к 16 видим существенное изменение наклона, которое говорит о том, что этот переход даёт несколько меньший выигрыш по времени по сравнению с предыдущими.

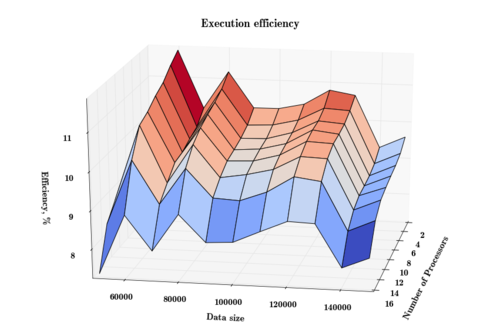
Вывод о понижении эффективности параллелизма с увеличением числа процессоров подтверждает и следующий график:

Рис.5. График эффективности программы в зависимости от числа процессов и размера задачи

Отметим, что в зависимости от количества точек (данных) графики производительности и эффективности ведут себя неустойчиво - это связано с нерегулярностью в алгоритме решения задачи, существенной зависимостью количества вычислений от структуры получающихся по ходу работы кластеров.

Масштабируемость программы описывается следующими вычисленными согласно предложенной методике ключевыми показателями:

• минимальная эффективность - 7,32%, максимальная эффективность - 11,75%. Как видим, в архитектуре с общей памятью удалось достичь весьма высоких показателей эффективности
• оценка масштабируемости по числу процессов: -0.00041 - данная цифра говорит о том, что при повышении числа процессов эффективность медленно падает. Это вызвано ростом накладных расходов на синхронизацию результатов, независимо полученных полученных процессорами.
• оценка масштабируемости по размеру задачи: 0.00002 - данная оценка имеет весьма большую дисперсию из-за наблюдаемых перепадов эффективности при изменении размерности задачи, однако в среднем с ростом задачи эффективность очень медленно растёт. Это подтверждает естественное соображение о том, что для больших задач использование параллелизма прирносит наибольшую пользу.
• оценка масштабируемости по двум направлениям: -0.00002 - при увеличении одновременно вычислительной сложности и числа процессоров имеем очень медленное убывание эффективности.

2.7 Существующие реализации алгоритма

Как правило, в библиотеках реализуют не собственно алгоритм кластеризации с использованием остовного дерева, а только алгоритм остовного дерева, предоставляя пользователю возможность самостоятельно реализовать функции построения графа и обработки результатов работы алгоритма.

Параллельная реализация алгоритма MST:

• C++, MPI: Parallel Boost Graph Library; функции dense_boruvka_minimum_spanning_tree, boruvka_then_merge, boruvka_mixed_merge сочетают алгоритм Борувки и алгоритм Крускала.

Последовательные реализации доступны во многих библиотеках:

• NetworkX MST - реализация в библиотеке для работы с графами на Python
• Алгоритм Прима, Алгоритм Крускала - C++ реализация в boost
• Алгоритм Прима, Алгоритм Крускала - Java реализация в JGraphT