Cholesky decomposition, scalability
Перейти к навигации
Перейти к поиску
Основные авторы описания: А.М.Теплов (раздел 3).
Содержание
1 Ссылки
Исследованная параллельная реализация на языке C.
2 Локальность данных и вычислений
2.1 Локальность реализации алгоритма
2.1.1 Структура обращений в память и качественная оценка локальности
2.1.2 Количественная оценка локальности
3 Масштабируемость алгоритма и его реализации
3.1 Масштабируемость алгоритма
3.2 Масштабируемость реализации алгоритма
Исследование проводилось на суперкомпьютере "Ломоносов"[1] Суперкомпьютерного комплекса Московского университета.
Проведём исследование масштабируемости параллельной реализации разложения Холецкого согласно методике.
Набор и границы значений изменяемых параметров запуска реализации алгоритма:
- число процессоров [4 : 256] с шагом 4;
- размер матрицы [1024 : 5120].
В результате проведённых экспериментов был получен следующий диапазон эффективности реализации алгоритма:
- минимальная эффективность реализации 0,11%;
- максимальная эффективность реализации 2,65%.
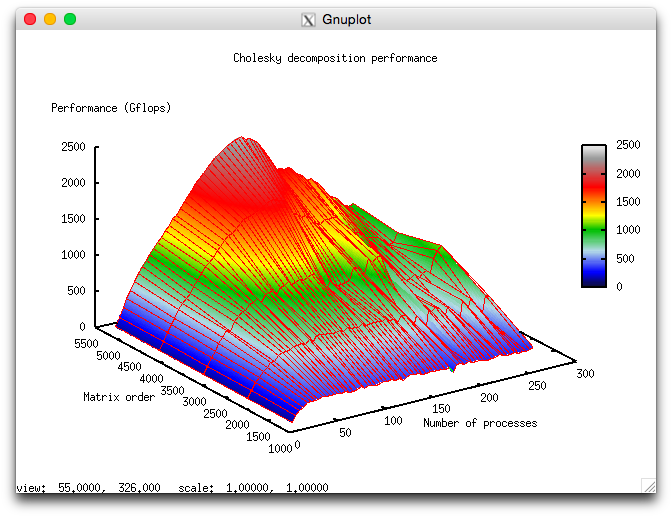
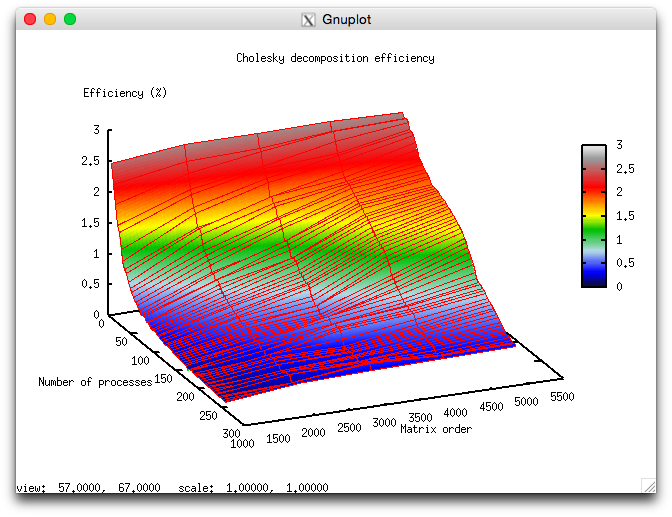
На следующих рисунках приведены графики производительности и эффективности выбранной реализации разложения Холецкого в зависимости от изменяемых параметров запуска.
Построим оценки масштабируемости выбранной реализации разложения Холецкого:
- По числу процессов: -0,000593. При увеличении числа процессов эффективность на рассмотренной области изменений параметров запуска уменьшается, однако в целом уменьшение не очень быстрое. Малая интенсивность изменения объясняется крайне низкой общей эффективностью работы приложения с максимумом в 2,65%, и значение эффективности на рассмотренной области значений быстро доходит до десятых долей процента. Это свидетельствует о том, что на большей части области значений нет интенсивного снижения эффективности. Это объясняется также тем, что с ростом вычислительной сложности падение эффективности становится не таким быстрым. Уменьшение эффективности на рассмотренной области работы параллельной программы объясняется быстрым ростом накладных расходов на организацию параллельного выполнения. С ростом вычислительной сложности задачи эффективность снижается так же быстро, но при больших значениях числа процессов. Это подтверждает предположение о том, что накладные расходы начинают сильно превалировать над вычислениями.
- По размеру задачи: 0,06017. При увеличении размера задачи эффективность возрастает. Эффективность возрастает тем быстрее, чем большее число процессов используется для выполнения. Это подтверждает предположение о том, что размер задачи сильно влияет на эффективность выполнения приложения. Оценка показывает, что с ростом размера задачи эффективность на рассмотренной области значений параметров запуска сильно увеличивается. Также, учитывая разницу максимальной и минимальной эффективности в 2,5%, можно сделать вывод, что рост эффективности при увеличении размера задачи наблюдается на большей части рассмотренной области значений.
- По двум направлениям: 0,000403. При рассмотрении увеличения как вычислительной сложности, так и числа процессов на всей рассмотренной области значений эффективность увеличивается, однако скорость увеличения эффективности небольшая. В совокупности с тем фактом, что разница между максимальной и минимальной эффективностью на рассмотренной области значений параметров небольшая, эффективность с увеличением масштабов возрастает, но медленно и с небольшими перепадами.
4 Динамические характеристики и эффективность реализации алгоритма
5 Результаты прогонов
6 Литература
- ↑ Воеводин Вл., Жуматий С., Соболев С., Антонов А., Брызгалов П., Никитенко Д., Стефанов К., Воеводин Вад. Практика суперкомпьютера «Ломоносов» // Открытые системы, 2012, N 7, С. 36-39.