Householder (reflections) reduction of a matrix to bidiagonal form, SCALAPACK

1 Ссылки

Для проведения экспериментов использовалась реализация Метод Хаусхолдера, представленная в пакете SCALAPACK библиотеки Intel MKL (метод pdgehrd).

3 Масштабируемость алгоритма и его реализации

3.2 Масштабируемость реализации алгоритма

Проведём исследование масштабируемости вширь реализации согласно методике. Исследование проводилось на суперкомпьютере "Ломоносов-2" Суперкомпьютерного комплекса Московского университета.

Набор и границы значений изменяемых параметров запуска реализации алгоритма:

• число процессоров [16:100] с шагом n^2;
• размер матрицы [1000 : 16000] с шагом 1000.

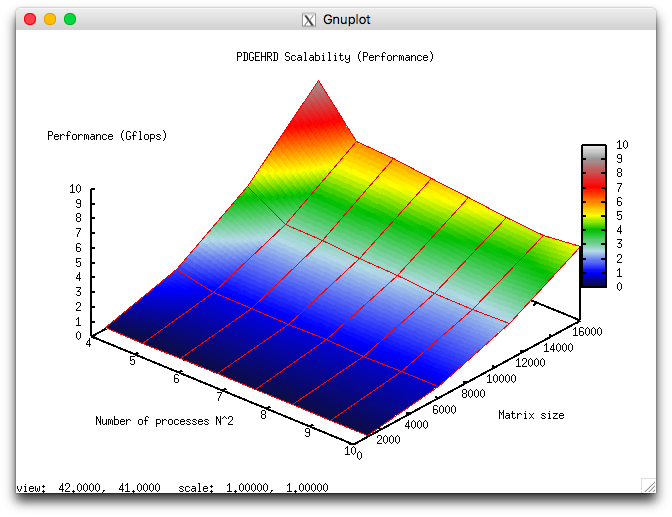
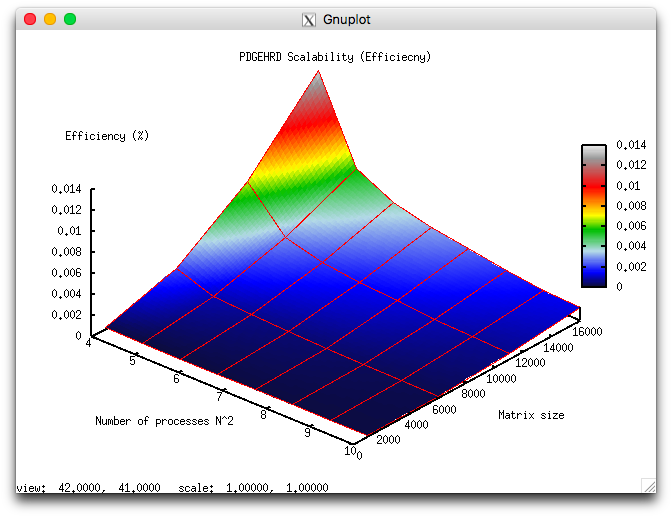
В результате проведённых экспериментов был получен следующий диапазон эффективности реализации алгоритма:

• минимальная эффективность реализации 5.033e-05%;
• максимальная эффективность реализации 0.0135%.

На следующих рисунках приведены графики производительности и эффективности выбранной реализации алгоритма в процедуре PDGEHRD из Scalapack в зависимости от изменяемых параметров запуска.

Рисунок 1. Параллельная реализация метода Хаусхолдера для приведения матриц к двухдиагональному виду. Изменение производительности в зависимости от числа процессоров и размера матрицы.

Рисунок 2. Параллельная реализация метода Хаусхолдера для приведения матриц к двухдиагональному виду. Изменение эффективности в зависимости от числа процессоров и размера матрицы.

4 Динамические характеристики и эффективность реализации алгоритма

Все результаты получены на суперкомпьютере «Ломоносов-2». Использовались процессоры Intel Xeon E5-2697v3, сеть FDR Infiniband а также компилятор Intel с опциями, рекомнедованными Intel MKL Advisor. На рисунках показана эффективность реализации метода Хаусхолдера (отражений) приведения матрицы к двухдиагональной форме для размерности матрицы 16000, запуск проводился на 100 ядрах.

Рисунок 3. График загрузки CPU при выполнении метода Хаусхолдера (отражений) приведения матрицы к двухдиагональной форме

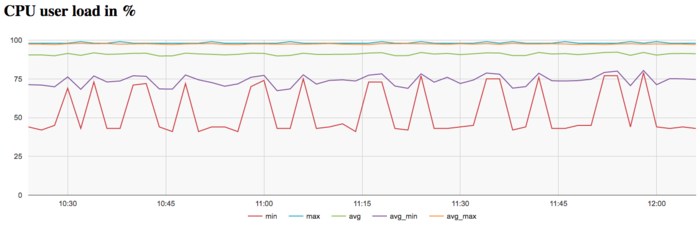
На графике загрузки процессора видно, что почти все время работы программы уровень загрузки составляет около 90%. Это хорошая картина для программ, запущенных c использованием технологии Hyper Threading т.е. всех виртуальных ядер доступных для данной архитектуры.

Рисунок 4. График числа процессов, ожидающих вхождения в стадию счета (Loadavg), при работе метода Хаусхолдера (отражений) приведения матрицы к двухдиагональной форме

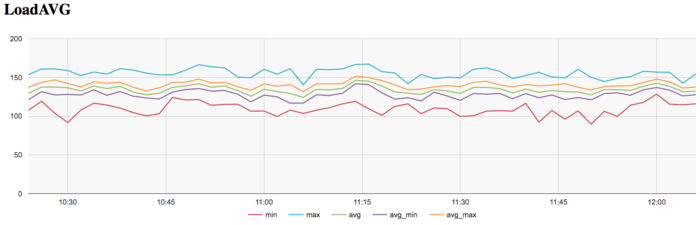
На графике числа процессов, ожидающих вхождения в стадию счета (Loadavg), видно, что на протяжении всей работы программы значение этого параметра постоянно и приблизительно равняется 140. Это свидетельствует о стабильной работе программы на протяжении всего выполнения со 140 нитями на одном узле или около 10 нитей на 1 физическое ядро на каждом узле. Это указывает на статичную загрузку аппаратных ресурсов процессами, однако их число для узла слишком велико, что с одной стороны может указывать на не очень рациональные опции компиляции, который могут приводить к снижению производительности из-за накладных расходов на переключение контекста между нитями.

Рисунок 5. График кэш-промахов L1 в секунду при работе метода Хаусхолдера (отражений) приведения матрицы к двухдиагональной формеy

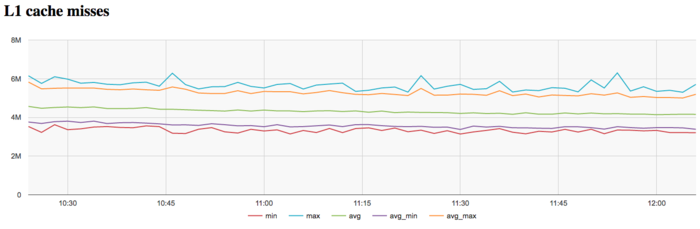
На графике кэш-промахов первого уровня видно, что число промахов достаточно низкое и находится на уровне 4 млн/сек в среднем по всем узлам. Интересен факт снижения числа промахов к концу итерации, хотя снижение и не очень значительное, но вполне заметное.

Рисунок 6. График кэш-промахов L1 в секунду при работе метода Хаусхолдера (отражений) приведения матрицы к двухдиагональной форме

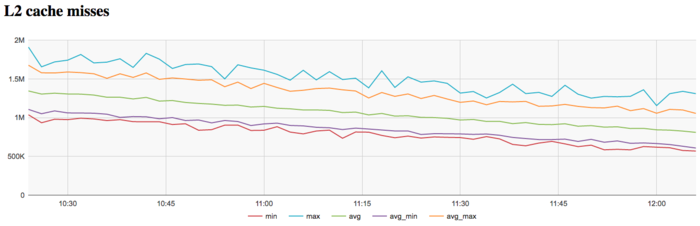
На графике кэш-промахов второго уровня видно, что число промахов достаточно тоже низкое и находится на уровне 1 млн/сек в среднем по всем узлам. На графике промахов второго уровня факт снижения числа промахов к концу итерации проявляется более явно и снижение и более значительное и заметное (с 1.4 млн до 0.8 млн.).

Рисунок 7. График кэш-промахов L3 в секунду при работе метода Хаусхолдера (отражений) приведения матрицы к двухдиагональной форме

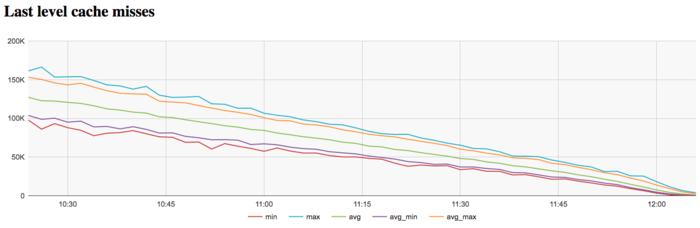
На графике кэш-промахов последнего уровня видно, что число промахов достаточно небольшое и быстро убывает с уровня 127 тыс/сек до 0 в среднем по всем узлам. Это указывает на то, что задача достаточно хорошо укладывается в кэш-память третьего уровня, особенно к концу итерации.

Рисунок 8. График скорости передачи по сети Infiniband в байт/сек при работе метода Хаусхолдера (отражений) приведения матрицы к двухдиагональной форме

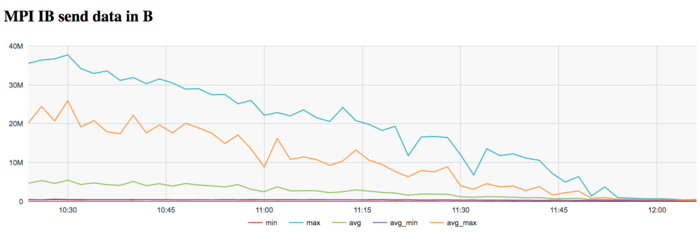
На графике скорости передачи данных по сети Infiniband наблюдается достаточно низкая интенсивность использования коммуникационной сети на каждой итерации. Причем к концу каждой итерации интенсивность передачи данных сильно снижается. Это указывает на бОльшую необходимость в обмене данными между процессами в начале итерации и большую локальность вычислений к концу итерации.

Рисунок 9. График скорости передачи по сети Infiniband в пакетах/сек при работе метода Хаусхолдера (отражений) приведения матрицы к двухдиагональной форме

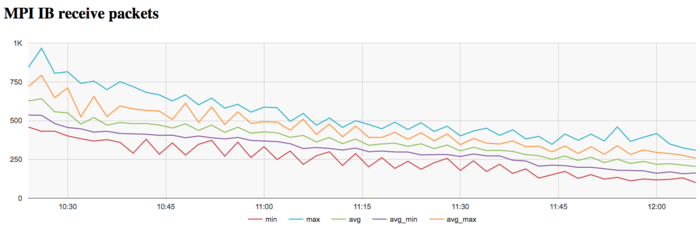
На графике скорости передачи данных в пакетах в секунду наблюдается большая «кучность» показаний максимального минимального и среднего значений в сравнении с графиком скорости передачи в байт/сек. Это говорит о том, что, вероятно, процессы обмениваются сообщениями различной длины, что указывает на неравномерное распределение данных. Также наблюдается рост интенсивности использования сети к концу каждой итерации. Особенно это различие заметно к концу итерации.

В целом, по данным системного мониторинга работы программы можно сделать вывод о том, что программа работала стабильно и эффективно использовала память. Использование памяти и коммуникационной среды не достаточно интенсивное, что может стать указывать на факторы снижения эффективности и увеличении производительности при существенном росте размера задачи. Для существующей в SCALAPACK параллельной реализаций характерно сильное снижение числа кэш-промахов и обменов к концу итерации