Уровень алгоритма

Участник:Potapyurich/Алгоритм концептуальной кластеризации COBWEB: различия между версиями

Материал из Алговики
Перейти к навигации Перейти к поиску
 
(не показано 107 промежуточных версий 5 участников)
Строка 1: Строка 1:
−
'(Здесь про нас и что мы работали вместе и сообща.
+
Авторы: [[Участник:potapyurich|Ю.Ю.Потапов]] (Разделы [[#Математическое описание алгоритма|1.2]], [[#Макроструктура алгоритма|1.4]], [[#Последовательная сложность алгоритма|1.6]], [[#Информационный граф|1.7]], [[#Ресурс параллелизма алгоритма|1.8]], [[#Свойства алгоритма|1.10]], [[#Существующие реализации алгоритма|2.7]]), [[Участник:Skripnikarthur|A.М.Скрипник]] (Разделы [[#Общее описание алгоритма|1.1]], [[#Вычислительное ядро алгоритма|1.3]], [[#Схема реализации последовательного алгоритма|1.5]], [[#Информационный граф|1.7]], [[#Входные и выходные данные алгоритма|1.9]], [[#Существующие реализации алгоритма|2.7]], )
 +
 
 +
<math> test1 math </math>
  
−
А также можно черкнуть про то, где этот алгоритм используется и каковы его преимущества, обзорненько.)'
 
  
 
{{algorithm
 
{{algorithm
 
| name              = Алгоритм концептуальной кластеризации COBWEB  
 
| name              = Алгоритм концептуальной кластеризации COBWEB  
−
| serial_complexity = <math>O(N^2\log N)</math>
+
| serial_complexity = <math> O(|C|*|A|*|V|*|O|)</math>
−
| pf_height        = <math>O(\log N)</math>
+
| input_data        = <math>|A|*|O|</math>
−
| pf_width          = <math>O(N^2)</math>
+
| output_data      = <math>|C|</math>
−
| input_data        = <math>O(N)</math>
 
−
| output_data      = <math>O(N)</math>
 
 
}}
 
}}
  
 
= ЧАСТЬ. Свойства и структура алгоритмов =
 
= ЧАСТЬ. Свойства и структура алгоритмов =
 
== Общее описание алгоритма ==
 
== Общее описание алгоритма ==
−
Задача кластеризации является одной из важнейших задач интеллектуального анализа данных в различных проблемных областях – технических, естественнонаучных, социальных. Кластеризация является примером задачи обучения без учителя и сводится к разбиению исходного множества объектов на подмножества классов таким образом, что элементы одного класса были бы схожи между собой, а элементы различных классов были бы максимально различны.[9]
+
Задача кластеризации является одной из важнейших задач интеллектуального анализа данных в различных проблемных областях – технических, естественнонаучных, социальных. Кластеризация является примером задачи обучения без учителя и сводится к разбиению исходного множества объектов на подмножества классов таким образом, что элементы одного класса были бы схожи между собой, а элементы различных классов были бы максимально различны.
  
−
COBWEB is an incremental system for hierarchical conceptual clustering. COBWEB was invented by Professor Douglas H. Fisher, currently at Vanderbilt University.[10]
+
Алгоритм COBWEB - классический метод инкрементальной концептуальной кластеризации, который был изобретен профессором Дугласом Фишером в 1987 году.
  
−
COBWEB incrementally organizes observations into a classification tree. Each node in a classification tree represents a class (concept) and is labeled by a probabilistic concept that summarizes the attribute-value distributions of objects classified under the node. This classification tree can be used to predict missing attributes or the class of a new object. [7]
+
В отличие от традиционной кластеризации, которая обнаруживает группы схожих объектов на основе меры сходства между ними, концептуальная кластеризация определяет кластеры как группы объектов, относящейся к одному классу или концепту – определённому набору пар "атрибут-значение". Алгоритм COBWEB создаёт иерархическую кластеризацию в виде дерева классификации: каждый узел этого дерева ссылается на концепт и содержит вероятностное описание этого концепта. Узлы, находящейся на определённом уровне дерева классификации, называют срезом. Алгоритм использует для построения дерева классификации эвристическую меру оценки, называемую полезностью категории – прирост ожидаемого числа корректных предположений о значениях атрибутов при знании об их принадлежности к определённой категории относительно ожидаемого числа корректных предположений о значениях атрибутов без этого знания. Чтобы встроить новый объект в дерево классификации, алгоритм COBWEB итеративно проходит всё дерево в поисках «лучшего» узла, к которому отнести этот объект. Выбор узла осуществляется на основе помещения объекта в каждый узел и вычисления полезности категории получившегося среза.
−
 
 
−
<< Сунуть пример с птичками-рыбками из [10] >>
 
−
 
 
−
Подробненькое словесное описание алгоритма. Наверное, с хабра [6] или из оригинала[10]
 
  
 
== Математическое описание алгоритма ==
 
== Математическое описание алгоритма ==
−
Математическое описание входных данных, выходных данных. формулка из [11] ( ну или из [10] повыдёргивать, если запариться. Но они там в итоге всё равно придут к конечной Функции полезности кластеризации )
+
* Обозначим: <math> O = \{O_1 \dots O_n\} </math> - множество распознаваемых объектов, характеризуемых аттрибутами <math> A = \{A_1 \dots A_m\} </math>, которые могут принимать значения <math> V = \{V_{11} \dots V_{mk}\} </math>. Ставится задача кластеризации исходного множеста объектов на классы <math> C = \{C_1 \dots C_l\} </math>  так, чтобы максимизировать функцию полезности кластеризации.
  
−
== Вычислительное ядро алгоритма ==
 
−
В описываемом алгоритме выделяется и описывается [[глоссарий#Вычислительное ядро|''вычислительное ядро'']], т.е. та часть алгоритма, на которую приходится основное время работы алгоритма. Если в алгоритме несколько вычислительных ядер, то отдельно описывается каждое ядро. Описание может быть сделано в достаточно произвольной форме: словесной или с использованием языка математических формул. Вычислительное ядро может полностью совпадать с описываемым алгоритмом.
 
  
−
== Макроструктура алгоритма ==
+
Полезность кластеризации рассматривается как функция CU, определяющая сходство объектов в рамках одного кластера, и их различие по отношению к объектам из других кластеров:
  
−
COBWEB incrementally incorporates objects into a classification tree,
+
<math> CU = \frac{\sum_{C_k \in C} P(C_k) [\sum_{i} \sum_{j} P(A_i = V_{ij} | C_k)^2 - \sum_{i} \sum_{j} P(A_i = V_{ij})^2]}{|C|} </math><br><br>
−
where each node is a probabilistic concept that represents an object class.
+
<math> P(A_i = V_{ij}) = \frac{|\{O_l | O_l \in C, A_i = V_{ij}\}|}{|\{O_l | O_l \in C\}|} </math><br><br>
−
The incorporation of an object is a process of classifying the object by
+
<math> P(A_i = V_{ij} | C_k) = \frac{|\{O_l | O_l \in C_k, A_i = V_{ij}\}|}{|\{O_l | O_l \in C_k\}|} </math><br><br>
−
descending the tree along an appropriate path, updating counts along the
 
−
way, and performing one of several operators at each level. These operators
 
−
include
 
−
• classifying the object with respect to an existing class,
 
−
• creating a new class,
 
−
• combining two classes into a single class, and
 
−
• dividing a class into several classes.
 
  
−
== Схема реализации последовательного алгоритма ==
+
При выполнении алгоритма итерационно строится дерево классификации. Каждая вершина дерева представляет собой класс. Срез дерева представляет возможное разбиение на непересекающииеся классы. Функция полезности CU применяется именно к срезу.<br><br>
−
Здесь описываются все шаги, которые нужно выполнить при последовательной реализации данного алгоритма. В некотором смысле, данный раздел является избыточным, поскольку математическое описание уже содержит всю необходимую информацию. Однако он, несомненно, полезен: схема реализации алгоритма выписывается явно, помогая однозначной интерпретации приводимых далее оценок и свойств.
+
Каждая вершина дерева содержит следующие данные:<br>
 +
<math>P(C_k)</math> - вероятность объекта принадлежать данному классу<br><math>P(A_i = V_{ij} | C_k)</math> - вероятность объекта иметь значение <math>V_{ij}</math> у аттрибута <math>A_i</math> при условии принадлежности к классу <math>C_k</math><br>
 +
<math>\{O_i\}</math> - множество объектов, принадлежащих данному классу.
  
−
Описание может быть выполнено в виде блок-схемы, последовательности математических формул, обращений к описанию других алгоритмов, фрагмента кода на Фортране, Си или другом языке программирования, фрагмента кода на псевдокоде и т.п. Главное - это сделать схему реализации последовательного алгоритма полностью понятной. Совершенно не обязательно все шаги детализировать до элементарных операций, отдельные шаги могут соответствовать макрооперациям, отвечающим другим алгоритмам.
 
  
−
Описание схемы реализации вполне может содержать и словесные пояснения, отражающие какие-либо тонкие нюансы самого алгоритма или его реализации. Уже в данном разделе можно сказать про возможный компромисс между объемом требуемой оперативной памяти и временем работы алгоритма, между используемыми структурами данных и степенью доступного параллелизма. В частности, часто возникает ситуация, когда можно ввести дополнительные временные массивы или же отказаться от использования специальных компактных схем хранения данных, увеличивая степень доступного параллелизма.
+
Алгоритм использует операции четырёх типов:
 +
* Отнесение объекта к существующему классу
 +
* Создание нового класса
 +
* Объединение двух классов в один
 +
* Разбиение одного класса на два
  
−
== Последовательная сложность алгоритма ==
+
Рис.1 показывает операции добавления нового класса и занесения объекта в существующий класс<br>
−
В данном разделе описания свойств алгоритма приводится оценка его [[глоссарий#Последовательная сложность|''последовательной сложности'']], т.е. числа операций, которые нужно выполнить при последовательном исполнении алгоритма (в соответствии с [[#Описание схемы реализации последовательного алгоритма|п.1.5]]). Для разных алгоритмов понятие операции, в терминах которой оценивается его сложность, может существенно различаться. Это могут быть операции для работы с вещественными числами, целыми числами, поразрядные операции, обращения в память, обновления элементов массива, элементарные функции, макрооперации и другие. В LU-разложении преобладают арифметические операции над вещественными числами, а для транспонирования матриц важны лишь обращения к памяти: это и должно найти отражение в описании.
+
Рис.2 показывает операции объединения<br>
 +
Рис.3 показывает разбиения классов
 +
{|align="center"
 +
|-valign="top"
 +
|[[Файл:cobweb_2.jpg|300px|thumb|center|Рис.1 a)Начальное состояние, b)Операция добавления нового класса, c)Операция занесения в существующий класс]]
 +
|[[Файл:cobweb_3.png|300px|thumb|center|Рис.2 Объединение двух классов в один]]
 +
|[[Файл:cobweb_4.png|300px|thumb|center|Рис.3 Разбиение одного класса на два]]
 +
|}
  
−
Если выбор конкретного типа операций для оценки сложности алгоритма не очевиден, то нужно привести обоснование возможных вариантов. В некоторых случаях можно приводить оценку не всего алгоритма, а лишь его вычислительного ядра: в таком случае это нужно отметить, сославшись [[#Общее описание алгоритма|на п.1.1]].
+
== Вычислительное ядро алгоритма ==
  
−
Например, сложность алгоритма суммирования элементов вектора сдваиванием равна <math>n-1</math>. Сложность быстрого преобразования Фурье (базовый алгоритм Кули-Тьюки) для векторов с длиной, равной степени двойки – <math>n\log_2n</math> операций комплексного сложения и <math>(n\log_2n)/2</math> операций комплексного умножения. Сложность базового алгоритма разложения Холецкого (точечный вариант для плотной симметричной и положительно-определенной матрицы) это <math>n</math> вычислений квадратного корня, <math>n(n-1)/2</math> операций деления, по <math>(n^3-n)/6</math> операций умножения и сложения (вычитания).
+
Вычислительное ядро алгоритма представляет собой итерационное вычисление всех параметров модели, так как вероятностное представление кластеров делает очень сложным их обновление, особенно в том случае, когда атрибуты имеют большое число возможных значений.
  
−
== Информационный граф ==
+
== Макроструктура алгоритма ==
−
Это очень важный раздел описания. Именно здесь можно показать (увидеть) как устроена параллельная структура алгоритма, для чего приводится описание и изображение его информационного графа ([[глоссарий#Граф алгоритма|''графа алгоритма'']] [1]). Для рисунков с изображением графа будут составлены рекомендации по их формированию, чтобы все информационные графы, внесенные в энциклопедию, можно было бы воспринимать и интерпретировать одинаково. Дополнительно можно привести полное параметрическое  описание графа в терминах покрывающих функций [1].
 
  
−
Интересных вариантов для отражения информационной структуры алгоритмов много. Для каких-то алгоритмов нужно показать максимально подробную структуру, а иногда важнее макроструктура. Много информации несут разного рода проекции информационного графа, выделяя его регулярные составляющие и одновременно скрывая несущественные детали. Иногда оказывается полезным показать последовательность в изменении графа при изменении значений внешних переменных  (например, размеров матриц): мы часто ожидаем "подобное" изменение информационного графа, но это изменение не всегда очевидно на практике. 
+
COBWEB поэлементно добавляет объекты в дерево классификации, где каждая вершина - это вероятностный концепт, который представляет класс. Добавление объекта - это процесс классификации этого объекта, спускаясь по дереву вдоль соответствующего пути, обновляя вероятностные характеристики классов на пути и выполняя одну из следующих операций на каждом уровне:
 +
* Отнесение объекта к существующему классу
 +
* Создание нового класса
 +
* Объединение двух классов в один
 +
* Разбиение одного класса на два
  
−
В целом, задача изображения графа алгоритма весьма нетривиальна. Начнем с того, что это потенциально бесконечный граф, число вершин и дуг которого определяется значениями внешних переменных, а они могут быть весьма и весьма велики. В такой ситуации, как правило, спасают упомянутые выше соображения подобия, делающие графы для разных значений внешних переменных "похожими": почти всегда достаточно привести лишь один граф небольшого размера, добавив, что графы для остальных значений будут устроены "точно также". На практике, увы, не всегда все так просто, и здесь нужно быть аккуратным.
+
== Схема реализации последовательного алгоритма ==
  
−
Далее, граф алгоритма - это потенциально многомерный объект. Наиболее естественная система координат для размещения вершин и дуг информационного графа опирается на структуру вложенности циклов в реализации алгоритма. Если глубина вложенности циклов не превышает трех, то и граф размещается в привычном трехмерном пространстве, однако для более сложных циклических конструкций с глубиной вложенности 4 и больше необходимы специальные методы представления и изображения графов.
+
# Используя первый объект Object, создаем корень дерева Root
 +
# COBWEB(Node, Object):
 +
## Если Node является листом дерева:
 +
### Cоздать два дочерних узла L1 и L2 для узла Node
 +
### Задать для узла L1 те же вероятности, что и для узла Node
 +
### Инициализировать вероятности для узла L2 соответствующими значениями объекта Object;
 +
### Добавить Object к Node, обновив вероятности для узла Node
 +
## Если Node не является листом:
 +
### Добавить Object к Node, обновив вероятности для узла Node
 +
### Для каждого дочернего узла <math>C</math> узла Node вычислить полезность категории при отнесении экземпляра Object к категории <math>C</math><br>пусть <math>S_1</math> - значение полезности для наилучшей классификации <math>C_1</math><br>пусть <math>S_2</math> - значение для второй наилучшей классификации <math>C_2</math><br>пусть <math>S_3</math> - значение полезности для отнесения экземпляра к новой категории<br>пусть <math>S_4</math> - значение для слияния <math>C_1</math> и <math>C_2</math> в одну категорию<br>пусть <math>S_5</math> - значение для разделения <math>C_1</math> (замены дочерними категориями)
 +
### Если <math>S_1</math> - максимальное значение, то отнести объект к <math>C_1</math>: COBWEB(<math>C_1</math>, Object)<br>Если <math>S_3</math> - максимальное значение, то инициализировать вероятности для новой категории <math>C_m</math> значениями Object<br>Если <math>S_4</math> - максимальное значение, то пусть <math>C_m</math> - результат слияния <math>C_1</math> и <math>C_2</math>: COBWEB(<math>C_m</math>, Object)<br>Если <math>S_5</math> - максимальное значение, то разделить <math>C_1</math> и для новой категории <math>C_m</math>: COBWEB(<math>C_m</math>, Object)
  
−
В данном разделе AlgoWiki могут использоваться многие интересные возможности, которые еще подлежат обсуждению: возможность повернуть граф при его отображении на экране компьютера для выбора наиболее удобного угла обзора, разметка вершин по типу соответствующим им операций, отражение [[глоссарий#Ярусно-параллельная форма графа алгоритма|''ярусно-параллельной формы графа'']] и другие. Но в любом случае нужно не забывать главную задачу данного раздела - показать информационную структуру алгоритма так, чтобы стали понятны все его ключевые особенности, особенности параллельной структуры, особенности множеств дуг, участки регулярности и, напротив, участки с недерминированной структурой, зависящей от входных данных.
+
== Последовательная сложность алгоритма ==
  
−
На рис.1 показана информационная структура алгоритма умножения матриц, на рис.2 - информационная структура одного из вариантов алгоритма решения систем линейных алгебраических уравнений с блочно-двухдиагональной матрицей.
+
Так как структура получаемого дерева зависит от входных данных, то сложность всего алгоритма оценить невозможно. Дерево может получиться либо хорошо сбалансированным, либо совсем разбалансированным. Это будет значительно влиять на общее количество итераций запуска рекурсивной функции.
  
−
[[file:Fig1.svg|thumb|center|300px|Рис.1. Информационная структура алгоритма умножения матриц]]
 
−
[[file:Fig2.svg|thumb|center|300px|Рис.2. Информационная структура одного из вариантов алгоритма решения систем линейных алгебраических уравнений с блочно-двухдиагональной матрицей]]
 
  
−
== Ресурс параллелизма алгоритма ==
+
Сложность вычисления <math> CU = \frac{\sum_{C_k \in C} P(C_k) [\sum_{i} \sum_{j} P(A_i = V_{ij} | C_k)^2 - \sum_{i} \sum_{j} P(A_i = V_{ij})^2]}{|C|} </math> - это <math> O(|C|*|A|*|V|*|O|)</math>, где<br>
−
Здесь приводится оценка [[глоссарий#Параллельная сложность|''параллельной сложности'']] алгоритма: числа шагов, за которое можно выполнить данный алгоритм в предположении доступности неограниченного числа необходимых процессоров (функциональных устройств, вычислительных узлов, ядер и т.п.). Параллельная сложность алгоритма понимается как высота канонической ярусно-параллельной формы [1]. Необходимо указать, в терминах каких операций дается оценка. Необходимо описать сбалансированность параллельных шагов по числу и типу операций, что определяется шириной ярусов канонической ярусно-параллельной формы и составом операций на ярусах.
 
  
−
Параллелизм в алгоритме часто имеет естественную иерархическую структуру. Этот факт очень полезен на практике, и его необходимо отразить в описании. Как правило, подобная иерархическая структура параллелизма хорошо отражается в последовательной реализации алгоритма через циклический профиль результирующей программы (конечно же, с учетом графа вызовов), поэтому циклический профиль ([[#Описание схемы реализации последовательного алгоритма|п.1.5]]) вполне  может быть использован и для отражения ресурса параллелизма.
+
*<math>|C|</math> - количество классов в срезе
 +
*<math>|A|</math> - количество аттрибутов объекта
 +
*<math>|V|</math> - количество возможных значений
 +
*<math>|O|</math> - количество объектов.
  
−
Для описания ресурса параллелизма алгоритма (ресурса параллелизма информационного графа) необходимо указать ключевые параллельные ветви в терминах [[глоссарий#Конечный параллелизм|''конечного'']] и [[глоссарий#Массовый параллелизм|''массового'']] параллелизма. Далеко не всегда ресурс параллелизма выражается просто, например, через [[глоссарий#Кооодинатный параллелизм|''координатный параллелизм'']] или, что то же самое, через независимость итераций некоторых циклов (да-да-да, циклы - это понятие, возникающее лишь на этапе реализации, но здесь все так связано… В данном случае, координатный параллелизм означает, что информационно независимые вершины лежат на гиперплоскостях, перпендикулярных одной из координатных осей). С этой точки зрения, не менее важен и ресурс [[глоссарий#Скошенный параллелизм|''скошенного параллелизма'']]. В отличие от координатного параллелизма, скошенный параллелизм намного сложнее использовать на практике, но знать о нем необходимо, поскольку иногда других вариантов и не остается: нужно оценить потенциал алгоритма, и лишь после этого, взвесив все альтернативы, принимать решение о конкретной параллельной реализации. Хорошей иллюстрацией может служить алгоритм, структура которого показана на рис.2: координатного параллелизма нет, но есть параллелизм скошенный, использование которого снижает сложность алгоритма с <math>n\times m</math> в последовательном случае до <math>(n+m-1)</math> в параллельном варианте.
+
== Информационный граф ==
−
 
+
На данном информационном графе изображен алгоритм выбора нужного действия при добавлении нового объекта в дерево классификации. А именно функция COBWEB, которая во время выполнения программы вызывается рекурсивно.
−
Рассмотрим алгоритмы, последовательная сложность которых уже оценивалась в [[#Последовательная сложность алгоритма|п.1.6]]. Параллельная сложность алгоритма суммирования элементов вектора сдваиванием равна <math>\log_2n</math>, причем число операций на каждом ярусе убывает с <math>n/2</math> до <math>1</math>. Параллельная сложность быстрого преобразования Фурье (базовый алгоритм Кули-Тьюки) для векторов с длиной, равной степени двойки - <math>\log_2n</math>. Параллельная сложность базового алгоритма разложения Холецкого (точечный вариант для плотной симметричной и положительно-определенной матрицы) это <math>n</math> шагов для вычислений квадратного корня, <math>(n-1)</math> шагов для операций деления и <math>(n-1)</math> шагов для операций умножения и сложения.
 
  
−
== Входные и выходные данные алгоритма ==
+
Входными данными являются текущий объект, который надо добавить, а также один из узлов дерева. На первой итерации это корень дерева.
−
В данном разделе необходимо описать объем, структуру, особенности и свойства входных и выходных данных алгоритма: векторы, матрицы, скаляры, множества, плотные или разреженные структуры данных, их объем. Полезны предположения относительно диапазона значений или структуры, например, диагональное преобладание в структуре входных матриц, соотношение между размером матриц по отдельным размерностям, большое число матриц очень малой размерности, близость каких-то значений к машинному нулю, характер разреженности матриц и другие.
 
  
−
== Свойства алгоритма ==
+
*Красные узлы графа - вычисление функции полезности CU после добавления объекта в один из узлов-потомков
−
Описываются прочие свойства алгоритма, на которые имеет смысл обратить внимание на этапе реализации. Как и ранее, никакой привязки к конкретной программно-аппаратной платформе не предполагается, однако вопросы реализации в проекте AlgoWiki всегда превалируют, и необходимость обсуждения каких-либо свойств алгоритмов определяется именно этим.
+
*Оранжевый - вычисление функции полезности CU после создания нового класса и добавления объекта в него
 +
*Фиолетовый - вычисление двух максимальных значений для CU
 +
*Желтый - вычисление функции полезности CU после объединения двух классов с максимальными функциями полезности
 +
*Коричневый - вычисление функции полезности CU после разбиения класса с максимальной функцией полезности
 +
*Голубой - выбрать действие, после которого функция полезности оказалась максимальной и вызвать рекурсивно функцию COBWEB от соответствующего узла и текущего объекта
  
−
Весьма полезным является ''соотношение последовательной и параллельной сложности'' алгоритма. Оба понятия мы рассматривали ранее, но здесь делается акцент на том выигрыше, который теоретически может дать параллельная реализация алгоритма. Не менее важно описать и те сложности, которые могут возникнуть в процессе получения параллельной версии алгоритма.
+
[[file:COBWEB_5.png|thumb|center|500px|Рис.4 Граф алгоритма COBWEB]]
  
−
[[глоссарий#Вычислительная мощность|''Вычислительная мощность'']] алгоритма равна отношению числа операций к суммарному объему входных и выходных данных. Она показывает, сколько операций приходится на единицу переданных данных. Несмотря на простоту данного понятия, это значение исключительно полезно на практике: чем выше  вычислительная мощность, тем меньше накладных расходов вызывает перемещение данных для их обработки, например, на сопроцессоре, ускорителе или другом узле кластера. Например, вычислительная мощность скалярного произведения двух векторов равна всего лишь <math>1</math>, а вычислительная мощность алгоритма умножения двух квадратных матриц равна <math>2n/3</math>.
+
== Ресурс параллелизма алгоритма ==
 +
Сложность одной итерации параллельного алгоритма будет определяться количеством вычислений функции полезности CU, которые невозможно выполнить параллельно.
  
−
Вопрос первостепенной важности на последующем этапе реализации - это [[глоссарий#Устойчивость|''устойчивость'']] алгоритма. Все, что касается различных сторон этого понятия, в частности, оценки устойчивости, должно быть описано в данном разделе.
+
Как видно на информационном графе, самая длинная ветвь алгоритма включает два вычисления функции CU (вычисление CU для одного из потомков и вычисление CU для объединения или разделения классов).<br>
 +
При этом параллельная ветвь, которая вычисляет только одну операцию CU для добавления нового класса, явно окажется несбалансированной с остальными ветками. Параллелизм, достигаемый при вычислении CU для всех предков узла является динамическим и зависит от структуры получаемого графа, то есть от входных данных - объектов.
  
−
''Сбалансированность'' вычислительного процесса можно рассматривать с разных сторон. Здесь и сбалансированность типов операций, в частности, арифметических операций между собой (сложение, умножение, деление) или же арифметических операций по отношению к операциям обращения к памяти (чтение/запись). Здесь и сбалансированность операций между параллельными ветвями алгоритма. С одной стороны, балансировка нагрузки является необходимым условием эффективной реализации алгоритма. Вместе с этим, это очень непростая задача, и в описании должно быть отмечено явно, насколько алгоритм обладает этой особенностью. Если обеспечение сбалансированности не очевидно, желательно описать возможные пути решения этой задачи.
+
Также, большой ресурс параллелизма заключается в самой операции <math> CU = \frac{\sum_{C_k \in C} P(C_k) [\sum_{i} \sum_{j} P(A_i = V_{ij} | C_k)^2 - \sum_{i} \sum_{j} P(A_i = V_{ij})^2]}{|C|} </math>, так как вычисление слагаемых суммы может происходить массово параллельно для всех возможных значений <math>A_i</math> и <math>V_{ij}</math> всех объектов <math>O_k \in C</math>
  
−
На практике важна [[глоссарий#Детерминированность|''детерминированность алгоритмов'']], под которой будем понимать постоянство структуры вычислительного процесса. С этой точки зрения, классическое умножение плотных матриц является детерминированным алгоритмом, поскольку его структура при фиксированном размере матриц никак не зависит от элементов входных матриц. Умножение разреженных матриц, когда матрица хранятся в одном из специальных форматов, свойством детерминированности уже не обладает: его свойства, например, степень локальности данных зависит от структуры разреженности входных матриц. Итерационный алгоритм с выходом по точности также не является детерминированным: число итераций, а значит и число операций, меняется в зависимости от входных данных. В этом же ряду стоит использование датчиков случайных чисел, меняющих вычислительный процесс для различных запусков программы. Причина выделения свойства детерминированности понятна: работать с детерминированным алгоритмом проще, поскольку один раз найденная структура и будет определять качество его реализации. Если детерминированность нарушается, то это должно быть здесь описано вместе с описанием того, как недетерминированность влияет на структуру вычислительного процесса.
+
== Входные и выходные данные алгоритма ==
  
−
Серьезной причиной недетерминированности работы параллельных программ является изменение порядка выполнения ассоциативных операций. Типичный пример - это использование глобальных MPI-операций на множестве параллельных процессов, например, суммирование элементов распределенного массива. Система времени исполнения MPI сама выбирает порядок выполнения операций, предполагая выполнение свойства ассоциативности, из-за чего ошибки округления меняются от запуска программы к запуску, внося изменения в конечный результат ее работы. Это очень серьезная проблема, которая сегодня встречается часто на системах с массовым параллелизмом и определяет отсутствие повторяемости результатов работы параллельных программ. Данная особенность характерна для [[#ЧАСТЬ. Программная реализация алгоритмов|второй части AlgoWiki]], посвященной реализации алгоритмов, но вопрос очень важный, и соответствующие соображения, по возможности, должны быть отмечены и здесь.
+
Так как основные операции выполняются над числами, интерпретирующими вероятности, то алгоритм оперирует данными примерно одного порядка точности.
  
−
Заметим, что, в некоторых случаях, недетерминированность в структуре алгоритмов можно "убрать" введением соответствующих макроопераций, после чего структура становится не только детерминированной, но и более понятной для восприятия. Подобное действие также следует отразить в данном разделе.
+
== Свойства алгоритма ==
  
−
[[глоссарий#Степень исхода|''Степень исхода вершины информационного графа'']] показывает, в скольких операциях ее результат будет использоваться в качестве аргумента. Если степень исхода вершины велика, то на этапе реализации алгоритма нужно позаботиться об эффективном доступе к результату ее работы. В этом смысле, особый интерес представляют рассылки данных, когда результат выполнения одной операции используется во многих других вершинах графа, причем число таких вершин растет с увеличением значения внешних переменных.
 
  
−
''"Длинные" дуги в информационном графе'' [1] говорят о потенциальных сложностях с размещением данных в иерархии памяти компьютера на этапе выполнения программы. С одной стороны, длина дуги зависит от выбора конкретной системы координат, в которой расположены вершины графа, а потому в другой системе координат они попросту могут исчезнуть (но не появится ли одновременно других длинных дуг?). А с другой стороны, вне зависимости от системы координат их присутствие может быть сигналом о необходимости длительного хранения данных на определенном уровне иерархии, что накладывает дополнительные ограничения на эффективность реализации алгоритма. Одной из причин возникновения длинных дуг являются рассылки скалярных величин по всем итерациям какого-либо цикла: в таком виде длинные дуги не вызывают каких-либо серьезных проблем на практике.
+
В узлах дерева хранится вероятностное распределение для всех возможных значений всех атрибутов объектов. Это сужает область применимости данного алгоритма. Для эффективного выполнения алгоритма, все объекты должны иметь атрибуты с небольшим набором возможных значений.
−
 
 
−
Для проектирования специализированных процессоров или реализации алгоритма на ПЛИС представляют интерес ''компактные укладки информационного графа'' [1], которые также имеет смысл привести в данном разделе.
 
  
 
= ЧАСТЬ. Программная реализация алгоритма =
 
= ЧАСТЬ. Программная реализация алгоритма =
−
Вторая часть описания алгоритмов в рамках AlgoWiki рассматривает все составные части процесса их реализации. Рассматривается как последовательная реализация алгоритма, так и параллельная. Описывается взаимосвязь свойств программ, реализующих алгоритм, и особенностей архитектуры компьютера, на которой они выполняются. Исследуется работа с памятью, локальность данных и вычислений, описывается масштабируемость и эффективность параллельных программ, производительность компьютеров, достигаемая на данной программе. Обсуждаются особенности реализации для разных классов архитектур компьютеров, приводятся ссылки на реализации в существующих библиотеках.
 
  
 
== Особенности реализации последовательного алгоритма ==
 
== Особенности реализации последовательного алгоритма ==
−
Здесь описываются особенности и варианты реализации алгоритма в виде последовательной программы, которые влияют на [[глоссарий#Эффективность реализации|''эффективность ее выполнения'']]. В частности, в данном разделе имеет смысл ''сказать о существовании блочных вариантов реализации алгоритма'', дополнительно описав потенциальные преимущества или недостатки, сопровождающие такую реализацию. Важный вопрос - это ''возможные варианты организации работы с данными'', варианты структур данных, наборов временных массивов и другие подобные вопросы. Для различных вариантов реализации следует оценить доступный ресурс параллелизма и объем требуемой памяти.
 
−
 
−
Важным нюансом является ''описание необходимой разрядности выполнения операций алгоритма'' (точности). На практике часто нет никакой необходимости выполнять все арифметические операции над вещественными числами с двойной точностью, т.к. это не влияет ни на устойчивость алгоритма, ни на точность получаемого результата. В таком случае, если значительную часть операций можно выполнять над типом float, и лишь в некоторых фрагментах необходим переход к типу double, это обязательно нужно отметить. Это прямое указание не только на правильную реализацию с точки зрения устойчивости по отношению к ошибкам округления, но и на более эффективную.
 
−
 
−
Опираясь на информацию из [[#Описание ресурса параллелизма алгоритма|п.1.8]] (описание ресурса параллелизма алгоритма), при описании последовательной версии стоит сказать про возможности [[глоссарий#Эквивалентное преобразование|''эквивалентного преобразования программ'']], реализующих данных алгоритм. В дальнейшем, это даст возможность простого использования доступного параллелизма или же просто покажет, как использовать присущий алгоритму параллелизм на практике. Например, параллелизм на уровне итераций самого внутреннего цикла обычно используется для векторизации. Однако, в некоторых случаях этот параллелизм можно поднять "вверх" по структуре вложенности объемлющих циклов, что делает возможной и эффективную реализацию данного алгоритма на многоядерных SMP-компьютерах.
 
−
 
−
С этой же точки зрения, в данном разделе весьма полезны соображения по реализации алгоритма на различных параллельных вычислительных платформах. Высокопроизводительные кластеры, многоядерные узлы, возможности для векторизации или использования ускорителей - особенности этих архитектур не только опираются на разные свойства алгоритмов, но и по-разному должны быть выражены в программах, что также желательно описать в данном разделе.
 
  
 
== [[Локальность данных и вычислений]] ==
 
== [[Локальность данных и вычислений]] ==
−
Вопросы локальности данных и вычислений не часто изучаются на практике, но именно локальность определяет эффективность выполнения программ на современных вычислительных платформах [2, 3]. В данном разделе приводятся оценки степени [[глоссарий#Локальность использования данных|''локальности данных'']] и [[глоссарий#Локальность вычислений|вычислений]] в программе, причем рассматривается как [[глоссарий#Временная локальность|''временна́я'']], так и [[глоссарий#Пространственная локальность|''пространственная'']] локальность. Отмечаются позитивные и негативные факты, связанные с локальностью, какие ситуации и при каких условиях могут возникать. Исследуется, как меняется локальность при переходе от последовательной реализации к параллельной. Выделяются ключевые шаблоны взаимодействия программы, реализующей описываемый алгоритм, с памятью. Отмечается возможная взаимосвязь между используемыми конструкциями языков программирования и степенью локальности, которыми обладают результирующие программы.
 
−
 
−
Отдельно приводятся профили взаимодействия с памятью для вычислительных ядер и ключевых фрагментов. Если из-за большого числа обращений по общему профилю сложно понять реальную специфику взаимодействия программ с памятью, то проводится последовательная детализация и приводится серия профилей более мелкого масштаба.
 
−
 
−
На рис.3 и рис.4 показаны профили обращения в память для программ, реализующих разложение Холецкого и быстрое преобразование Фурье, по которым хорошо видна разница свойств локальности у данных алгоритмов.
 
−
 
−
[[file:Cholesky_locality1.jpg|thumb|center|700px|Рис.3 Реализация метода Холецкого. Общий профиль обращений в память]]
 
−
[[file:fft 1.PNG|thumb|center|700px|Рис.4 Нерекурсивная реализация БПФ для степеней двойки. Общий профиль обращений в память]]
 
  
 
== Возможные способы и особенности параллельной реализации алгоритма ==
 
== Возможные способы и особенности параллельной реализации алгоритма ==
−
Раздел довольно обширный, в котором должны быть описаны основные факты и положения, формирующие параллельную программу. К их числу можно отнести:
 
−
* представленный иерархически ресурс параллелизма, опирающийся на структуру циклических конструкций и на граф вызовов программы;
 
−
* комбинацию (иерархию) массового параллелизма и параллелизма конечного;
 
−
* возможные способы распределения операций между процессами/нитями;
 
−
* возможные способы распределения данных;
 
−
* оценку количества операций, объёма и числа пересылок данных (как общего числа, так и в пересчёте на каждый параллельный процесс);
 
−
 
−
и другие.
 
−
 
−
В этом же разделе должны быть даны рекомендации или сделаны комментарии относительно реализации алгоритма с помощью различных технологий параллельного программирования: MPI, OpenMP, CUDA или использования директив векторизации.
 
  
 
== Масштабируемость алгоритма и его реализации ==
 
== Масштабируемость алгоритма и его реализации ==
−
Задача данного раздела - показать пределы [[глоссарий#Масштабируемость|''масштабируемости'']] алгоритма на различных платформах. Очень важный раздел. Нужно выделить, описать и оценить влияние точек барьерной синхронизации, глобальных операций, операций сборки/разборки данных, привести оценки или провести исследование [[глоссарий#Сильная масштабируемость|''сильной'']] и [[глоссарий#Слабая масштабируемость|''слабой'']] масштабируемости алгоритма и его реализаций.
 
−
 
−
Масштабируемость алгоритма определяет свойства самого алгоритма безотносительно конкретных особенностей используемого компьютера. Она показывает, насколько параллельные свойства алгоритма позволяют использовать возможности растущего числа процессорных элементов. Масштабируемость параллельных программ определяется как относительно конкретного компьютера, так и относительно используемой технологии программирования, и в этом случае она показывает, насколько может вырасти реальная производительность данного компьютера на данной программе, записанной с помощью данной технологии программирования, при использовании бóльших вычислительных ресурсов (ядер, процессоров, вычислительных узлов).
 
−
 
−
Ключевой момент данного раздела заключается в том, чтобы показать ''реальные параметры масштабируемости программы'' для данного алгоритма на различных вычислительных платформах в зависимости от числа процессоров и размера задачи  [4]. При этом важно подобрать такое соотношение между числом процессоров и размером задачи, чтобы отразить все характерные точки в поведении параллельной программы, в частности, достижение максимальной производительности, а также тонкие эффекты, возникающие, например, из-за блочной структуры алгоритма или иерархии памяти.
 
−
 
−
На рис.5. показана масштабируемость классического алгоритма умножения плотных матриц в зависимости от числа процессоров и размера задачи. На графике хорошо видны области с большей производительностью, отвечающие уровням кэш-памяти.
 
−
[[file:Масштабируемость перемножения матриц производительность.png|thumb|center|700px|Рис.5 Масштабируемость классического алгоритма умножения плотных матриц в зависимости от числа процессоров и размера задачи]]
 
  
 
== Динамические характеристики и эффективность реализации алгоритма ==
 
== Динамические характеристики и эффективность реализации алгоритма ==
−
Это объемный раздел AlgoWiki, поскольку оценка эффективности реализации алгоритма требует комплексного подхода [5], предполагающего аккуратный анализ всех этапов от архитектуры компьютера до самого алгоритма. Основная задача данного раздела заключается в том, чтобы оценить степень эффективности параллельных программ, реализующих данный алгоритм на различных платформах, в зависимости от числа процессоров и размера задачи. Эффективность в данном разделе понимается широко: это и [[глоссарий#Эффективность распараллеливания|''эффективность распараллеливания'']] программы, это и [[глоссарий#Эффективность реализации|''эффективность реализации'']] программ по отношению к пиковым показателям работы вычислительных систем.
 
−
 
−
Помимо собственно показателей эффективности, нужно описать и все основные причины, из-за которых эффективность работы параллельной программы на конкретной вычислительной платформе не удается сделать выше. Это не самая простая задача, поскольку на данный момент нет общепринятой методики и соответствующего инструментария, с помощью которых подобный анализ можно было бы провести. Требуется оценить и описать эффективность работы с памятью (особенности профиля взаимодействия программы с памятью), эффективность использования заложенного в алгоритм ресурса параллелизма, эффективность использования коммуникационной сети (особенности коммуникационного профиля), эффективность операций ввода/вывода и т.п. Иногда достаточно интегральных характеристик по работе программы, в некоторых случаях полезно показать данные мониторинга нижнего уровня, например, по загрузке процессора, кэш-промахам, интенсивности использования сети Infiniband и т.п. Хорошее представление о работе параллельной MPI-программы дают данные трассировки, полученные, например, с помощью системы Scalasca.
 
  
 
== Выводы для классов архитектур ==
 
== Выводы для классов архитектур ==
−
В данный раздел должны быть включены рекомендации по реализации алгоритма для разных классов архитектур. Если архитектура какого-либо компьютера или платформы обладает специфическими особенностями, влияющими на эффективность реализации, то это здесь нужно отметить.
 
−
 
−
На практике это сделать можно по-разному: либо все свести в один текущий раздел, либо же соответствующие факты сразу включать в предшествующие разделы, где они обсуждаются и необходимы по смыслу. В некоторых случаях, имеет смысл делать отдельные варианты всей [[#ЧАСТЬ. Программная реализация алгоритмов|части II]] AlgoWiki применительно к отдельным классам архитектур, оставляя общей машинно-независимую [[#ЧАСТЬ. Свойства и структура алгоритмов|часть I]]. В любом случае, важно указать и позитивные, и негативные факты по отношению к конкретным классам. Можно говорить о возможных вариантах оптимизации или даже о "трюках" в написании программ, ориентированных на целевые классы архитектур.
 
  
 
== Существующие реализации алгоритма ==
 
== Существующие реализации алгоритма ==
−
Для многих пар алгоритм+компьютер уже созданы хорошие реализации, которыми можно и нужно пользоваться на практике. Данный раздел предназначен для того, чтобы дать ссылки на основные существующие последовательные и параллельные реализации алгоритма, доступные для использования уже сейчас. Указывается, является ли реализация коммерческой или свободной, под какой лицензией распространяется, приводится местоположение дистрибутива и имеющихся описаний. Если есть информация об особенностях, достоинствах и/или недостатках различных реализаций, то это также нужно здесь указать. Хорошими примерами реализации многих алгоритмов являются MKL, ScaLAPACK, PETSc, FFTW, ATLAS, Magma и другие подобные библиотеки.
 
  
−
= Литература =
+
Существуют следующие реализации алгоритма COBWEB:
−
[1] Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. - СПб.: БХВ-Петербург, 2002. - 608 с.
+
* [https://github.com/cmaclell/concept_formation/ concept_formation] библиотека реализации алгоритмов COBWEB и COBWEB/3 для языка Python.
 +
* [http://www.cs.waikato.ac.nz/~ml/weka Weka] библиотека и инструмент для анализа данных на языке Java.
 +
* [http://java-ml.sourceforge.net/ Java-ML] библиотека машинного обучения на языке Java.
  
−
[2] Воеводин В.В., Воеводин Вад.В. Спасительная локальность суперкомпьютеров //Открытые системы. - 2013. - № 9. - С. 12-15.
+
Так как существуют алгоритмы кластеризации, обладающие лучшими свойствами, алгоритм COBWEB практически не применяется и параллельных реализаций этого алгоритма нет.
  
−
[3] Воеводин Вад.В., Швец П. Метод покрытий для оценки локальности использования данных в программах // Вестник УГАТУ. — 2014. — Т. 18, № 1(62). — С. 224–229.
+
= Литература =
−
 
 
−
[4] Антонов А.С., Теплов А.М. О практической сложности понятия масштабируемости параллельных программ// Высокопроизводительные параллельные вычисления на кластерных системах (HPC 2014): Материалы XIV Международной конференции -Пермь: Издательство ПНИПУ, 2014. С. 20-27.
 
−
 
 
−
[5] Никитенко Д.А. Комплексный анализ производительности суперкомпьютерных систем, основанный на данных системного мониторинга // Вычислительные методы и программирование. 2014. 15. 85–97.
 
−
 
 
−
[6] Обзор алгоритмов кластеризации числовых пространств данных: https://habrahabr.ru/post/164417/
 
  
−
[7] Wiki: https://en.wikipedia.org/wiki/Cobweb_(clustering)
+
[1] Fisher D. Knowledge Acquisition Via Incremental Conceptual Clustering, 1987. – P. 142–153. - http://link.springer.com/article/10.1007/BF00114265
  
−
[8] Java implementation: http://weka.sourceforge.net/doc.dev/weka/clusterers/Cobweb.html
+
[2] Методы и средства анализа данных - Алгоритм Cobweb: http://bourabai.ru/tpoi/analysis6.htm#.D0.90.D0.BB.D0.B3.D0.BE.D1.80.D0.B8.D1.82.D0.BC_Cobweb
  
−
[9] МОДЕЛЬ И МЕТОД КОНЦЕПТУАЛЬНОЙ КЛАСТЕРИЗАЦИИ ОБЪЕКТОВ, ХАРАКТЕРИЗУЕМЫХ НЕЧЕТКИМИ ПАРАМЕТРАМИ // Фундаментальные исследования. – 2014. – № 9 (часть 5) – С. 993-997 - http://www.fundamental-research.ru/ru/article/view?id=35003
+
[3] МОДЕЛЬ И МЕТОД КОНЦЕПТУАЛЬНОЙ КЛАСТЕРИЗАЦИИ ОБЪЕКТОВ, ХАРАКТЕРИЗУЕМЫХ НЕЧЕТКИМИ ПАРАМЕТРАМИ // Фундаментальные исследования. – 2014. – № 9 (часть 5) – С. 993-997 - http://www.fundamental-research.ru/ru/article/view?id=35003
  
−
[10] Fisher D. Knowledge Acquisition Via Incremental Conceptual Clustering, 1987. – P. 142–153. - http://link.springer.com/article/10.1007/BF00114265
+
[4] Обзор алгоритмов кластеризации числовых пространств данных: https://habrahabr.ru/post/164417/
  
−
[11] Методы и средства анализа данных - Алгоритм Cobweb: http://bourabai.ru/tpoi/analysis6.htm#.D0.90.D0.BB.D0.B3.D0.BE.D1.80.D0.B8.D1.82.D0.BC_Cobweb
+
[5] Wiki: https://en.wikipedia.org/wiki/Cobweb_(clustering)
  
 
[[en:Description of algorithm properties and structure]]
 
[[en:Description of algorithm properties and structure]]

Текущая версия на 01:50, 24 января 2017

Авторы: Ю.Ю.Потапов (Разделы 1.2, 1.4, 1.6, 1.7, 1.8, 1.10, 2.7), A.М.Скрипник (Разделы 1.1, 1.3, 1.5, 1.7, 1.9, 2.7, )

[math] test1 math [/math]



Алгоритм концептуальной кластеризации COBWEB
Последовательный алгоритм
Последовательная сложность [math] O(|C|*|A|*|V|*|O|)[/math]
Объём входных данных [math]|A|*|O|[/math]
Объём выходных данных [math]|C|[/math]


1 ЧАСТЬ. Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Задача кластеризации является одной из важнейших задач интеллектуального анализа данных в различных проблемных областях – технических, естественнонаучных, социальных. Кластеризация является примером задачи обучения без учителя и сводится к разбиению исходного множества объектов на подмножества классов таким образом, что элементы одного класса были бы схожи между собой, а элементы различных классов были бы максимально различны.

Алгоритм COBWEB - классический метод инкрементальной концептуальной кластеризации, который был изобретен профессором Дугласом Фишером в 1987 году.

В отличие от традиционной кластеризации, которая обнаруживает группы схожих объектов на основе меры сходства между ними, концептуальная кластеризация определяет кластеры как группы объектов, относящейся к одному классу или концепту – определённому набору пар "атрибут-значение". Алгоритм COBWEB создаёт иерархическую кластеризацию в виде дерева классификации: каждый узел этого дерева ссылается на концепт и содержит вероятностное описание этого концепта. Узлы, находящейся на определённом уровне дерева классификации, называют срезом. Алгоритм использует для построения дерева классификации эвристическую меру оценки, называемую полезностью категории – прирост ожидаемого числа корректных предположений о значениях атрибутов при знании об их принадлежности к определённой категории относительно ожидаемого числа корректных предположений о значениях атрибутов без этого знания. Чтобы встроить новый объект в дерево классификации, алгоритм COBWEB итеративно проходит всё дерево в поисках «лучшего» узла, к которому отнести этот объект. Выбор узла осуществляется на основе помещения объекта в каждый узел и вычисления полезности категории получившегося среза.

1.2 Математическое описание алгоритма

  • Обозначим: [math] O = \{O_1 \dots O_n\} [/math] - множество распознаваемых объектов, характеризуемых аттрибутами [math] A = \{A_1 \dots A_m\} [/math], которые могут принимать значения [math] V = \{V_{11} \dots V_{mk}\} [/math]. Ставится задача кластеризации исходного множеста объектов на классы [math] C = \{C_1 \dots C_l\} [/math] так, чтобы максимизировать функцию полезности кластеризации.


Полезность кластеризации рассматривается как функция CU, определяющая сходство объектов в рамках одного кластера, и их различие по отношению к объектам из других кластеров:

[math] CU = \frac{\sum_{C_k \in C} P(C_k) [\sum_{i} \sum_{j} P(A_i = V_{ij} | C_k)^2 - \sum_{i} \sum_{j} P(A_i = V_{ij})^2]}{|C|} [/math]

[math] P(A_i = V_{ij}) = \frac{|\{O_l | O_l \in C, A_i = V_{ij}\}|}{|\{O_l | O_l \in C\}|} [/math]

[math] P(A_i = V_{ij} | C_k) = \frac{|\{O_l | O_l \in C_k, A_i = V_{ij}\}|}{|\{O_l | O_l \in C_k\}|} [/math]

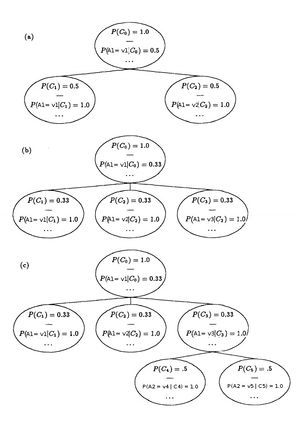
При выполнении алгоритма итерационно строится дерево классификации. Каждая вершина дерева представляет собой класс. Срез дерева представляет возможное разбиение на непересекающииеся классы. Функция полезности CU применяется именно к срезу.

Каждая вершина дерева содержит следующие данные:
[math]P(C_k)[/math] - вероятность объекта принадлежать данному классу
[math]P(A_i = V_{ij} | C_k)[/math] - вероятность объекта иметь значение [math]V_{ij}[/math] у аттрибута [math]A_i[/math] при условии принадлежности к классу [math]C_k[/math]
[math]\{O_i\}[/math] - множество объектов, принадлежащих данному классу.


Алгоритм использует операции четырёх типов:

  • Отнесение объекта к существующему классу
  • Создание нового класса
  • Объединение двух классов в один
  • Разбиение одного класса на два

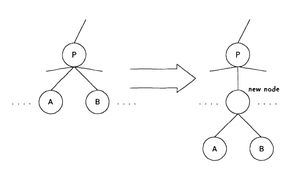
Рис.1 показывает операции добавления нового класса и занесения объекта в существующий класс
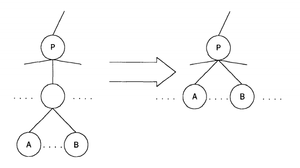
Рис.2 показывает операции объединения
Рис.3 показывает разбиения классов

Рис.1 a)Начальное состояние, b)Операция добавления нового класса, c)Операция занесения в существующий класс
Рис.2 Объединение двух классов в один
Рис.3 Разбиение одного класса на два

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма представляет собой итерационное вычисление всех параметров модели, так как вероятностное представление кластеров делает очень сложным их обновление, особенно в том случае, когда атрибуты имеют большое число возможных значений.

1.4 Макроструктура алгоритма

COBWEB поэлементно добавляет объекты в дерево классификации, где каждая вершина - это вероятностный концепт, который представляет класс. Добавление объекта - это процесс классификации этого объекта, спускаясь по дереву вдоль соответствующего пути, обновляя вероятностные характеристики классов на пути и выполняя одну из следующих операций на каждом уровне:

  • Отнесение объекта к существующему классу
  • Создание нового класса
  • Объединение двух классов в один
  • Разбиение одного класса на два

1.5 Схема реализации последовательного алгоритма

  1. Используя первый объект Object, создаем корень дерева Root
  2. COBWEB(Node, Object):
    1. Если Node является листом дерева:
      1. Cоздать два дочерних узла L1 и L2 для узла Node
      2. Задать для узла L1 те же вероятности, что и для узла Node
      3. Инициализировать вероятности для узла L2 соответствующими значениями объекта Object;
      4. Добавить Object к Node, обновив вероятности для узла Node
    2. Если Node не является листом:
      1. Добавить Object к Node, обновив вероятности для узла Node
      2. Для каждого дочернего узла [math]C[/math] узла Node вычислить полезность категории при отнесении экземпляра Object к категории [math]C[/math]
        пусть [math]S_1[/math] - значение полезности для наилучшей классификации [math]C_1[/math]
        пусть [math]S_2[/math] - значение для второй наилучшей классификации [math]C_2[/math]
        пусть [math]S_3[/math] - значение полезности для отнесения экземпляра к новой категории
        пусть [math]S_4[/math] - значение для слияния [math]C_1[/math] и [math]C_2[/math] в одну категорию
        пусть [math]S_5[/math] - значение для разделения [math]C_1[/math] (замены дочерними категориями)
      3. Если [math]S_1[/math] - максимальное значение, то отнести объект к [math]C_1[/math]: COBWEB([math]C_1[/math], Object)
        Если [math]S_3[/math] - максимальное значение, то инициализировать вероятности для новой категории [math]C_m[/math] значениями Object
        Если [math]S_4[/math] - максимальное значение, то пусть [math]C_m[/math] - результат слияния [math]C_1[/math] и [math]C_2[/math]: COBWEB([math]C_m[/math], Object)
        Если [math]S_5[/math] - максимальное значение, то разделить [math]C_1[/math] и для новой категории [math]C_m[/math]: COBWEB([math]C_m[/math], Object)

1.6 Последовательная сложность алгоритма

Так как структура получаемого дерева зависит от входных данных, то сложность всего алгоритма оценить невозможно. Дерево может получиться либо хорошо сбалансированным, либо совсем разбалансированным. Это будет значительно влиять на общее количество итераций запуска рекурсивной функции.


Сложность вычисления [math] CU = \frac{\sum_{C_k \in C} P(C_k) [\sum_{i} \sum_{j} P(A_i = V_{ij} | C_k)^2 - \sum_{i} \sum_{j} P(A_i = V_{ij})^2]}{|C|} [/math] - это [math] O(|C|*|A|*|V|*|O|)[/math], где

  • [math]|C|[/math] - количество классов в срезе
  • [math]|A|[/math] - количество аттрибутов объекта
  • [math]|V|[/math] - количество возможных значений
  • [math]|O|[/math] - количество объектов.

1.7 Информационный граф

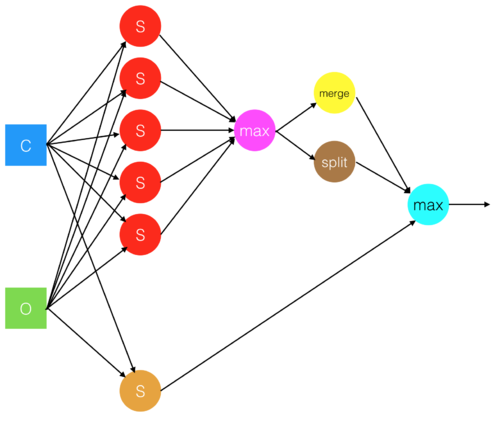
На данном информационном графе изображен алгоритм выбора нужного действия при добавлении нового объекта в дерево классификации. А именно функция COBWEB, которая во время выполнения программы вызывается рекурсивно.

Входными данными являются текущий объект, который надо добавить, а также один из узлов дерева. На первой итерации это корень дерева.

  • Красные узлы графа - вычисление функции полезности CU после добавления объекта в один из узлов-потомков
  • Оранжевый - вычисление функции полезности CU после создания нового класса и добавления объекта в него
  • Фиолетовый - вычисление двух максимальных значений для CU
  • Желтый - вычисление функции полезности CU после объединения двух классов с максимальными функциями полезности
  • Коричневый - вычисление функции полезности CU после разбиения класса с максимальной функцией полезности
  • Голубой - выбрать действие, после которого функция полезности оказалась максимальной и вызвать рекурсивно функцию COBWEB от соответствующего узла и текущего объекта
Рис.4 Граф алгоритма COBWEB

1.8 Ресурс параллелизма алгоритма

Сложность одной итерации параллельного алгоритма будет определяться количеством вычислений функции полезности CU, которые невозможно выполнить параллельно.

Как видно на информационном графе, самая длинная ветвь алгоритма включает два вычисления функции CU (вычисление CU для одного из потомков и вычисление CU для объединения или разделения классов).
При этом параллельная ветвь, которая вычисляет только одну операцию CU для добавления нового класса, явно окажется несбалансированной с остальными ветками. Параллелизм, достигаемый при вычислении CU для всех предков узла является динамическим и зависит от структуры получаемого графа, то есть от входных данных - объектов.

Также, большой ресурс параллелизма заключается в самой операции [math] CU = \frac{\sum_{C_k \in C} P(C_k) [\sum_{i} \sum_{j} P(A_i = V_{ij} | C_k)^2 - \sum_{i} \sum_{j} P(A_i = V_{ij})^2]}{|C|} [/math], так как вычисление слагаемых суммы может происходить массово параллельно для всех возможных значений [math]A_i[/math] и [math]V_{ij}[/math] всех объектов [math]O_k \in C[/math]

1.9 Входные и выходные данные алгоритма

Так как основные операции выполняются над числами, интерпретирующими вероятности, то алгоритм оперирует данными примерно одного порядка точности.

1.10 Свойства алгоритма

В узлах дерева хранится вероятностное распределение для всех возможных значений всех атрибутов объектов. Это сужает область применимости данного алгоритма. Для эффективного выполнения алгоритма, все объекты должны иметь атрибуты с небольшим набором возможных значений.

2 ЧАСТЬ. Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

2.2 Локальность данных и вычислений

2.3 Возможные способы и особенности параллельной реализации алгоритма

2.4 Масштабируемость алгоритма и его реализации

2.5 Динамические характеристики и эффективность реализации алгоритма

2.6 Выводы для классов архитектур

2.7 Существующие реализации алгоритма

Существуют следующие реализации алгоритма COBWEB:

  • concept_formation библиотека реализации алгоритмов COBWEB и COBWEB/3 для языка Python.
  • Weka библиотека и инструмент для анализа данных на языке Java.
  • Java-ML библиотека машинного обучения на языке Java.

Так как существуют алгоритмы кластеризации, обладающие лучшими свойствами, алгоритм COBWEB практически не применяется и параллельных реализаций этого алгоритма нет.

3 Литература

[1] Fisher D. Knowledge Acquisition Via Incremental Conceptual Clustering, 1987. – P. 142–153. - http://link.springer.com/article/10.1007/BF00114265

[2] Методы и средства анализа данных - Алгоритм Cobweb: http://bourabai.ru/tpoi/analysis6.htm#.D0.90.D0.BB.D0.B3.D0.BE.D1.80.D0.B8.D1.82.D0.BC_Cobweb

[3] МОДЕЛЬ И МЕТОД КОНЦЕПТУАЛЬНОЙ КЛАСТЕРИЗАЦИИ ОБЪЕКТОВ, ХАРАКТЕРИЗУЕМЫХ НЕЧЕТКИМИ ПАРАМЕТРАМИ // Фундаментальные исследования. – 2014. – № 9 (часть 5) – С. 993-997 - http://www.fundamental-research.ru/ru/article/view?id=35003

[4] Обзор алгоритмов кластеризации числовых пространств данных: https://habrahabr.ru/post/164417/

[5] Wiki: https://en.wikipedia.org/wiki/Cobweb_(clustering)

Источник — https://algowiki-project.org/w/ru/index.php?title=Участник:Potapyurich/Алгоритм_концептуальной_кластеризации_COBWEB&oldid=21692