Участник:Amirida/Метод «разделяй и властвуй» вычисления собственных значений и векторов симметричной трехдиагональной матрицы

Метод «разделяй и властвуй» вычисления собственных значений и векторов симметричной трехдиагональной матрицы.

Авторы:

Изотова И.А. (619 группа) пункты 1.1, 1.2, 1.5, 1.7, 1.9

Ульянов Г.В. (619 группа) пункты 1.3, 1.4, 1.6, 1.8, 1.10

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

«Разделяй и властвуй» - метод вычисления собственных значений и векторов симметричной трехдиагональной матрицы. В настоящее время это один из самых быстрых методов при вычислении собственных значений и векторов симметричной трехдиагональной матрицы порядка [math]n \gt 25[/math] (точное значение этого порогового порядка зависит от компьютера.) Однако алгоритм не гарантирует высокой относительной точности для малых собственных значений.Его численно устойчивая реализация весьма не тривиальна. Хотя впервые метод был предложен еще в 1981 г., "правильный" способ его реализации был найден лишь в 1992 г. Этот способ воплощен LAPACK-программами ssyevd (для плотных матриц) и sstevd (для трехдиагональных матриц). В них стратегия "разделяй-и-влавствуй" используется для матриц порядка, большего чем 25. Для матриц меньшего порядка (или если нужны только собственные значения) происходит автоматический переход к QR-итерации. Однако, из-за высокой сложности, алгоритм пока не вошел в состав ALGLIB.

В наихудшем случае алгоритм «разделяй-и-властвуй» требует [math] O(n^{3})[/math] операций, но константа, на практике оказывается весьма малой. На большой выборке случайных тестовых матриц в среднем затрачивается лишь [math] O(n^{2.3})[/math] операций с плавающей точкой, а для некоторых специальных распределений собственных значений — [math] O(n^{2})[/math] (подробнее в разделе 1.6 Последовательная сложность алгоритма).

1.2 Математическое описание алгоритма

Разделяй

Пусть матрицы [math]T, T_{1}[/math], [math]T_{2}[/math] имеют размерность [math]n \times n[/math], [math]m \times m[/math], [math](n - m) \times (n - m)[/math].

Запишем матрицу [math]T[/math] в следующем виде:

[math] T = \begin{bmatrix} a_{1} & b_{1}&&&&& \\ b_{1} & \ddots & \ddots \\ & \ddots & a_{m-1} & b_{m-1} \\ && b_{m-1} & a_{m} & b_{m} \\ &&& b_{m} & a_{m+1} & b_{m+1} \\ &&&& b_{m+1} & \ddots \\ &&&&&& \ddots & b_{n-1} \\ &&&&&& b_{n-1} & a_{n} \\ \end{bmatrix} = \begin{bmatrix} a_{1} & b_{1} &&&&& \\ b_{1} & \ddots & \ddots \\ & \ddots & a_{m-1} & b_{m-1} \\ && b_{m-1} & a_{m} - b_{m} \\ &&&& a_{m+1} - b_{m} & b_{m+1} \\ &&&& b_{m+1} & \ddots \\ &&&&&& \ddots & b_{n-1} \\ &&&&&& b_{n-1} & a_{n} \\ \end{bmatrix} + [/math]

[math] + \begin{bmatrix} b_{m} & b_{m} \\ b_{m} & b_{m} \\ \end{bmatrix} = \begin{bmatrix} T_{1} & 0 \\ 0 & T_{2} \end{bmatrix} + b_{m} * \begin{bmatrix} 0 \\ \vdots \\ 0 \\ 1 \\ 1 \\ 0 \\ \vdots \\ 0 \end{bmatrix} \begin{bmatrix} 0 , \ldots , 0 , 1 , 1 , 0 \ldots , 0 \end{bmatrix} \equiv \begin{bmatrix} T_{1} & 0 \\ 0 & T_{2}\end{bmatrix} + b_{m}vv^{T} [/math]

Предположим, что нам известны спектральные разложения матриц [math]\hat{T}_{1}[/math] и [math]\hat{T}_{2}[/math], т.е.: [math]\hat{T}_{1} = Q_{1} D_{1} Q_{1}^{T}[/math] и [math]\hat{T}_{2} = Q_{2} D_{2} Q_{2}^{T}[/math].

Властвуй

Установим связь между собственными значениями матрицы [math]T[/math] и собственными значениями матриц [math]T_{1}[/math] и [math]T_{2}[/math]:

[math] T = \begin{bmatrix} T_{1} & 0 \\ 0 & T_{2}\end{bmatrix} + b_{m}vv^{T} = \begin{bmatrix} Q_{1} \Lambda_{1} Q_{1}^{T} & 0 \\ 0 & Q_{2} L_{2} Q_{2}^{T}\end{bmatrix} + b_{m}vv^{T} = \begin{bmatrix} Q_{1} & 0 \\ 0 & Q_{2}\end{bmatrix}(\begin{bmatrix} \Lambda_{1} & \\ & \Lambda_{2}\end{bmatrix} + b_{m}vv^{T})\begin{bmatrix} Q_{1}^{T} & 0 \\ 0 & Q_{2}^{T}\end{bmatrix} [/math],

где [math] u = \begin{bmatrix} Q_{1}^{T} & 0 \\ 0 & Q_{2}^{T}\end{bmatrix}v [/math] - матрица, в первой строке которой находятся элементы последнего столбца матрицы [math] Q_{1}^{T}[/math], а во второй - элементы первого столбца матрицы [math] Q_{2}^{T}[/math], так как [math]v = \begin{bmatrix} 0 , \ldots , 0 , 1 , 1 , 0 \ldots , 0 \end{bmatrix}^T[/math]. Следовательно, [math]T[/math] имеет такие же собственные значения, что и подобная ей матрица [math]D + \rho uu^{T}[/math], где [math]D = \begin{bmatrix} L_{1} & 0 \\ 0 & L_{2}\end{bmatrix}[/math] - диагональная матрица, [math]\rho = b_{m}[/math] - число, а [math]u[/math] - вектор. В дальнейшем предполагаем, не ограничивая общности, что диагональные элементы [math]d_{1}, \ldots, d_{n}[/math] матрицы [math]D[/math] упорядочены по не возрастанию: [math]d_{n} \lt = \ldots \lt =d_{1}[/math].

Для того, чтобы найти собственные значения матрицы [math]D + \rho uu^{T}[/math], потребуется вычислить её характеристический многочлен, считая пока матрицу [math]D - \lambda I[/math] невырожденной. Тогда получаем [math]det(D + \rho uu^{T} - \lambda I) = det((D - \lambda I)(I + \rho (D- \lambda I)^{-1} uu^{T}))[/math].

Так как [math]D - \lambda I[/math] невырожденная, [math]det(I + \rho (D - \lambda I)^{-1}uu^{T}) = 0[/math] тогда и только тогда, когда [math]\lambda[/math] - является собственным значением. Можем заметить, что матрица [math]I + \rho (D - \lambda I)^{-1}uu^{T}[/math] получается из единичной путём добавления матрицы ранга 1. Определитель такой матрицы не сложно вычислить.

 Лемма 1. Справедливо равенство [math]det(I + xy^{T}) = 1 + y^{T}x[/math], где [math]x[/math] и [math]y[/math] - векторы.

Следовательно, получаем [math]det(I + \rho (D - \lambda I)^{-1}uu^{T}) = 1 + \rho u^{T}(D - \lambda I)^{-1}u[/math] [math] = 1 + \rho \sum_{i=1, n} \frac{u_{i}^{2}} {d_{i}-\lambda} \equiv f(\lambda)[/math] ,

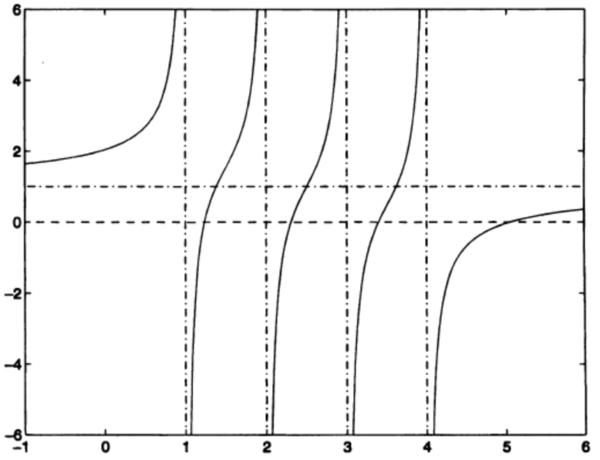
т.е. собственные значения матрицы [math]T[/math] являются корнями так называемого векового уравнения [math]f(\lambda) = 0[/math]. Если все числа [math]d_{i}[/math] различны между собой и все [math]u_{i} \lt \gt 0[/math] (случай общего положения), то [math]f(\lambda)[/math] имеет график типа, который показан на рис.1(где [math]n = 4[/math] и [math]\rho \gt 0[/math]).

Рис. 1. График функции [math] f(\lambda) = 1 + \frac{0.5}{1 - \lambda} + \frac{0.5}{2 - \lambda} + \frac{0.5}{3 - \lambda} + \frac{0.5}{4 - \lambda}[/math]

По Рис.1 можно заметить, что прямая [math]y = 1[/math] является горизонтальной асимптотой для данного графика, а прямые [math]\lambda = d_{i}[/math] есть вертикальные асимптоты. Так как [math]f^{'}(\lambda) = \rho \sum_{i=1, n} \frac{u_{i}^{2}} {(d_{i}-\lambda)^{2}}\gt 0 [/math], функция возрастает всюду, кроме точек [math]\lambda = d_{i}[/math]. Из этого следует, что корни функции разделяются числами [math]d_{i}[/math] и ещё один корень находится справа от точки [math]d_{1}[/math] (на рис. 1 [math]d_{1} = 4[/math]). (При [math]\rho\lt 0[/math] функция [math]f(\lambda)[/math] всюду убывает и соответствующий корень будет находиться слева от точки [math]d_{n}[/math]). Для функции [math]f(\lambda)[/math], которая является монотонной и гладкой на каждом из интервалов [math](d_{i+1},d_{i})[/math], можно найти вариант метода Ньютона, который будет быстро и монотонно сходиться к каждому из корней, при условии, что начальная точка взята в [math](d_{i+1},d_{i})[/math]. Нам достаточно знать тот факт, что на практике метод сходится к каждому собственному значению за строго ограниченное число шагов. Поскольку вычисление [math]f(\lambda)[/math] и [math]f^{'}(\lambda)[/math] стоит [math]O(n)[/math] флопов, для вычисления одного собственного значения достаточно [math]O(n)[/math] флопов, следовательно для вычисления всех [math]n[/math] собственных значений матрицы [math]D + \rho uu^{T}[/math] потребуется [math]O(n^{2})[/math] флопов. Для собственных векторов матрицы [math]D + \rho uu^{T}[/math] мы легко можем получить явные выражения.

 Лемма 2. Если [math]\alpha[/math] - собственное значение матрицы [math]D + \rho uu^{T}[/math], то соответствующий вектор равен [math](D - \alpha I)^{-1}u[/math]. Поскольку матрица [math]D - \alpha I[/math] диагональная, для вычисления такого вектора достаточно [math]O(n)[/math] флопов.

Доказательство:

[math](D + \rho uu^{T})[(D - \alpha I)^{-1}u] = (D - \alpha I + \alpha I + \rho uu^{T})(D - \alpha I)^{-1}u = u + \alpha (D - \alpha I)^{-1}u + u[\rho u^{T}(D - \alpha I)^{-1}u]= [/math]

[math] = u + \alpha(D - \alpha I)^{-1}u - u = \alpha [(D - \alpha I)^{-1}u][/math],

поскольку

[math] \rho u^{T}(D - \alpha I)^{-1}u + 1 = f(\alpha) = 0 [/math].

Что и требовалось доказать.

Получается, что для вычисления по этой простой формуле всех [math]n[/math] собственных векторов потребуется [math]O(n^{2})[/math] флопов. К сожалению, данная формула не обеспечивает нам численной устойчивости, так как для двух очень близких значений [math]\alpha_{i}[/math] может давать неортогональные приближенные собственные векторы [math]u_{i}[/math]. Учёным потребовалось целое десятилетие для того, чтобы найти устойчивую альтернативу исходному описанию алгоритма. Подробнее детали будут обсуждаться ниже в данном разделе.

1.3 Вычислительное ядро алгоритма

Вычислительным ядром последовательной схемы решения будет являться вычисление матрицы [math]Q[/math] собственных векторов при помощи умножения матрицы [math]Q = \begin{bmatrix} Q_{1} & 0 \\ 0 & Q_{2}\end{bmatrix}[/math] на матрицу [math]Q^{'}[/math]. Эта операция имеет сложность [math]cn^{3}[/math] о чём будет говориться ниже, в разделе 1.6 Последовательная сложность алгоритма .

Данной операции предшествует вычисление собственных значений и векторов матрицы [math] D + \rho uu^{T}[/math].

1.4 Макроструктура алгоритма

Дефляция

До сих пор полагалось, что все [math]d_{i}[/math] различны и все [math]u_{i}[/math] отличны от нуля. Если это не так, вековое уравнение [math]f(\lambda)=0[/math] имеет [math]k[/math] вертикальных асимптот, где [math]k\lt n[/math], а потому [math]k[/math] корней. Однако оказывается, что остальные [math]n - k[/math] собственных значений могут быть определены без каких-либо усилий: если [math]d_{i}=d_{i+1}[/math] или [math]u_{i}=0[/math], то легко показать, что [math]d_{i}[/math] является собственным значением и для матрицы [math]D + \rho uu^{T}[/math]. В такой ситуации мы говорим о дефляции. На практике выбирается некоторое пороговое значение и дефляция для числа [math]d_{i}[/math] регистрируется, если в смысле этого порога [math]d_{i}[/math] достаточно близко к [math]d_{i+1}[/math] либо [math]u_{i}[/math] достаточно мало.

Основной выигрыш от использования дефляции состоит не в том, что убыстряется решение векового уравнения - этот этап в любом случае стоит лишь [math]O(n^{2})[/math] операций. Выигрыш заключается в ускорении матричного умножения на последнем шаге алгоритма. Действительно, если [math]u_{i}=0[/math], то соответствующий собственный вектор есть i-й столбец [math]e_{i}[/math] единичной матрицы. Это означает, что [math]e_{i}[/math] является i-м столбцом в матрице [math]Q_{'}[/math], поэтому при формировании матрицы [math]Q[/math] посредством левого умножения [math]Q_{1}[/math] на [math]Q_{2}[/math] вычисление i-го столбца не требует никаких затрат. Аналогичное упрощение имеет место в случае [math]d_{i} = d_{i+1}[/math]. При дефляции многих собственных значений устраняется большая часть работы, связанной с матричным умножением.

Метод Ньютона

Далее пойдет речь о решении векового уравнения, которое является одной из основных частей алгоритма.

Предположим, что некоторое [math]u_{i}[/math], хотя и мало, все же недостаточно мало для того, чтобы была зарегистрирована дефляция. В этом случае применение метода Ньютона к решению векового уравнения встречается с затруднениями. Вспомним, что пересчет приближённого решения [math]u_{j}[/math] уравнения [math]f(\lambda) = 0[/math] в методе Ньютона основан на следующих положениях:

1. Вблизи точки [math]\lambda = \lambda_{j}[/math] функция [math]f(\lambda)[/math] аппроксимируется линейной функцией [math]l(\lambda)[/math]; график есть прямая линия, касающаяся графика функции [math]f(\lambda)[/math] при [math]\lambda = \lambda_{j}[/math].

2. В качестве [math]\lambda_{j+1}[/math] берётся нуль этого линейного приближения, т.е. [math]l(\lambda_{j+1})=0[/math].

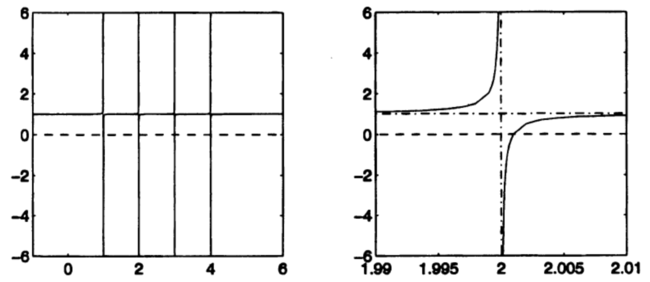
Функция, показанная на рис.1, не доставляет видимых трудностей методу Ньютона, поскольку вблизи каждого своего нуля [math]f(\lambda)[/math] достаточно хорошо аппроксимируется линейными функциями. Однако рассмотрим график функции на рис. 2. Она получена из функции на рис. 1 заменой значения .5 для [math]u_{i}^{2}[/math] на .001. Это новое значение недостаточно мало для того, чтобы вызвать дефляцию. График функции в левой части рис.2 визуально не отличим от её вертикальных и горизонтальных асимптот, поэтому в правой части укрупненно воспроизведён фрагмент графика, прилегающий к вертикальной асимптоте [math]\lambda = 2[/math]. Видно, что график слишком быстро "выполняет поворот" и для большей части значений [math]\lambda[/math] почти горизонтален. Поэтому, применяя метод Ньютона почти к любому начальному приближению [math]\lambda_{0}[/math], мы получаем линейное приближение [math]l(\lambda)[/math] с почти горизонтальным графиком и малым положительным угловым коэффициентом. В результате [math]\lambda_{1}[/math] является отрицательным числом, огромным по абсолютной величине, которое совершенно бесполезно в качестве приближения к истинному корню.

Рис. 2. График функции [math] f(\lambda) = 1 + \frac{10^{-3}}{1 - \lambda} + \frac{10^{-3}}{2 - \lambda} + \frac{10^{-3}}{3 - \lambda} + \frac{10^{-3}}{4 - \lambda}[/math]

Чтобы найти выход из этого положения, можно модифицировать метод Ньютона следующим образом: раз [math]f(\lambda)[/math] нельзя хорошо приблизить линейной функцией [math]l(\lambda)[/math], попробуем взять в качестве приближения какую-нибудь другую простую функцию [math]h(\lambda)[/math]. Нет ничего особого именно в прямых линиях: для метода Ньютона вместо [math]l(\lambda)[/math] можно взять любое приближение [math]h(\lambda)[/math], значения и нули которого легко вычисляются. Функция [math]f(\lambda)[/math] имеет полюсы в точках [math]d_{i}[/math] и [math]d_{i+1}[/math], которые определяют её поведение в соответствующих окрестностях. Поэтому при поиске корня в интервале [math](d_{i+1}, d_{i})[/math] естественно выбрать функцию [math]h(\lambda)[/math], также имеющую эти полюсы, т.е. функцию вида [math]h(\lambda)= \frac{c_{1}}{d_{i}-\lambda} + \frac{c_{2}}{d_{i+1}-\lambda} + c_{3}[/math]

Константы [math]c_{1},c_{2}[/math] и [math]c_{3}[/math] обеспечивающие, что [math]h(\lambda)[/math] есть приближение к [math]f(\lambda)[/math], можно выбрать несколькими способами. Отметим, что если [math]c_{1},c_{2}[/math] и [math]c_{3}[/math] уже известны, то уравнение [math]h(\lambda)=0[/math] легко решается относительно [math]\lambda[/math], поскольку сводится к эквивалентному квадратному уравнению [math]c_{1}(d_{i+1}-\lambda)+c_{2}(d_{i}-\lambda)+c_{3}(d_{i}-\lambda)(d_{i+1}-\lambda)=0[/math]

Пусть [math]\lambda_{j}[/math] - приближённое значение корня. определим [math]c_{1},c_{2}[/math] и [math]c_{3}[/math] так, чтобы [math]\frac{c_{1}}{d_{i}-\lambda} + \frac{c_{2}}{d_{i+1}-\lambda} + c_{3} = h(\lambda) \approx f(\lambda) = 1 + \rho \sum_{k=1, n} \frac{u_{k}^{2}} {d_{k}-\lambda} [/math] для [math]\lambda[/math] в окрестности [math]\lambda_{j}[/math]. Заметим, что [math]f(\lambda) = 1 + \rho \sum_{k=1, i} \frac{u_{k}^{2}} {d_{k}-\lambda} + \rho \sum_{k=i+1, n} \frac{u_{k}^{2}} {d_{k}-\lambda} \equiv 1 + \psi_{1}(\lambda) + \psi_{2}(\lambda)[/math].

Если [math]\lambda \in (d_{i+1},d_{i})[/math], то [math]\psi_{1}(\lambda)[/math] есть сумма положительных слагаемых, а [math]\psi_{2}(\lambda)[/math] - сумма отрицательных. Поэтому и [math]\psi_{1}(\lambda)[/math], и [math]\psi_{2}(\lambda)[/math] могут быть вычислены с высокой точностью; однако при их сложении вполне вероятно взаимное уничтожение верных разрядов и потеря относительной точности в сумме. Возьмем числа [math]c_{1}[/math] и [math]\hat{c_{1}}[/math], такие, что функция [math]h_{1}(\lambda) \equiv \hat{c_{1}} + \frac{c_{1}}{d_{i}-\lambda}[/math] удовлетворяет условиям [math]h_{1}(\lambda_{j}) = \psi_{1}(\lambda_{j})[/math] и [math]h_{1}^{'}(\lambda_{j})=\psi_{1}^{'}(\lambda_{j})[/math] (*)

Это означает, что гипербола, являющаяся графиком функции [math]h_{1}(\lambda)[/math], касается графика функции [math]\psi_{i}(\lambda)[/math] при [math]\lambda = \lambda_{j}[/math]. Два условия в (*) - это обычные условия метода Ньютона, за исключением того, что вместо прямой в качестве приближения используется гипербола. Легко проверить, что [math]c_{1}=\psi_{1}^{'}(\lambda_{j})(d_{i} - \lambda_{j})^{2}[/math] и [math]\hat{c_{1}}=\psi_{1}(\lambda_{j}) - \psi_{1}^{'}(\lambda_{j})(d_{i} - \lambda_{j})[/math].

Подобным же образом выбираем [math]c_{2}[/math] и [math]\hat{c_{2}}[/math] так, чтобы функция [math]h_{2}(\lambda) \equiv \hat{c_{2}} + \frac{c_{2}}{d_{i+1}-\lambda}[/math] удовлетворяла условиям [math]h_{2}(\lambda_{j}) = \psi_{2}(\lambda_{j})[/math] и [math]h_{2}^{'}(\lambda_{j})=\psi_{2}^{'}(\lambda_{j})[/math]

Наконец, полагаем [math]h(\lambda) = 1 + h_{1}(\lambda) + h_{2}(\lambda) = (1 + \hat{c_{1}} + \hat{c_{2}} + \frac{c_{1}}{d_{i}-\lambda} + \frac{c_{2}}{d_{i+1}-\lambda} \equiv c_{3} + \frac{c_{1}}{d_{i}-\lambda} + \frac{c_{2}}{d_{i+1}-\lambda}[/math].

Как только из векового уравнения найдены собственные значения [math]\alpha_{i}[/math] матрицы [math]D + \rho uu^{T}[/math], можно вычислить собственные векторы, пользуясь просто формулой [math](D - \alpha_{i})^{-1}u[/math] и из Леммы 2.К сожалению, вычисления по этой формуле могут быть неустойчивы. Так будет, в частности, когда собственные значения [math]\alpha_{i}[/math], [math]\alpha_{i+1}[/math] очень близки. Интуитивно проблема состоит в том, что выражения [math](D - \alpha_{i})^{-1}u[/math] и [math](D - \alpha_{i+1})^{-1}u[/math] "очень похожи", в то время как требуется получить ортогональные собственные векторы. Более точно, если [math]\alpha_{i}[/math] и [math]\alpha_{i+1}[/math] очень близки, оба близки к находящемуся между ними числу [math]d_{i}[/math]. Поэтому имеет место заметная потеря верных знаков при вычислении [math]d_{i} - \alpha_{i+1}[/math] или [math]\alpha_{i+1} - d_{i}[/math], либо при решении векового уравнения методом Ньютона. В любом из этих случаев [math]d_{i} - \alpha_{i}[/math] и [math]\alpha_{i+1} - d_{i}[/math] могут содержать большие относительные ошибки, вследствие чего вычисленные собственные векторы [math](D - \alpha_{i})^{-1}u[/math] и [math](D - \alpha_{i+1})^{-1}u[/math] и очень неточны, и далеки от ортогональности.

1.5 Схема реализации последовательного алгоритма

Рассмотри реализацию метода "разделяй и властвуй" в виде алгоритма:

proc dc_eig [math](T, Q, \Lambda) ... [/math] по входной матрице [math]T[/math] вычисляются выходные матрицы [math]Q[/math] и [math]\Lambda[/math], такие, что [math]T = Q\Lambda Q^{T}[/math]
    if матрица [math]T[/math] имеет размерность [math]1 \times 1[/math], then
        присвоить выходным параметрам значения [math]Q = 1, \Lambda = T[/math]
    else
        [math]T[/math] в виде [math] T = \begin{bmatrix} T_{1} & 0 \\ 0 & T_{2}\end{bmatrix} + b_{m}vv^{T} [/math]
        call dc_eig[math](T_{1},Q_{1},\Lambda_{1})[/math]
        call dc_eig[math](T_{2},Q_{2},\Lambda_{2})[/math]
        [math]D+\rho uu^{T}[/math] по [math] \Lambda_{1},\Lambda_{2}, Q_{1}, Q_{2}[/math]
        Найти матрицу собственных значений [math]\Lambda[/math]
        Найти матрицу собственных векторов [math]Q^{'}[/math] для матрицы [math]D+\rho uu^{T}[/math]
        Построить матрицу собственных векторов [math]Q[/math] для матрицы [math]T[/math] : [math] Q = \begin{bmatrix} Q_{1} & 0 \\ 0 & 
Q_{2}\end{bmatrix}* Q^{'} [/math]
        Присвоить выходным параметрам значения [math]Q[/math] и [math]\Lambda[/math]
 endif

1.6 Последовательная сложность алгоритма

Пусть [math]t(n)[/math] - число флопов при обработке матрицы размера [math]n \times n[/math] процедурой dc_eig. Тогда

[math]t(n) = 2t(n/2)[/math] два рекурсивных обращения к dc_eig[math](T_{i},Q_{i},\Lambda_{i})[/math]

[math]+O(n^{2})[/math] вычисление собственных значений матрицы [math]D+\rho uu^{T}[/math]

[math]+O(n^{2})[/math] вычисление собственных векторов матрицы [math]D+\rho uu^{T}[/math]

[math]+c*n^{3}[/math] вычисление матрицы [math]Q = \begin{bmatrix} Q_{1} & 0 \\ 0 & Q_{2}\end{bmatrix}*Q^{'}[/math]

Если [math] Q_{1}, Q_{2}[/math] и [math]Q^{'}[/math] рассматриваются как плотные матрицы и используется стандартный алгоритм матричного умножения, то константа [math] c [/math] в последней строке равна 1. Таким образом, именно это умножение составляет наиболее трудоёмкую часть алгоритма в целом. Игнорируя члены порядка [math]n^{2}[/math], получаем [math]t(n) = 2t(n/2) + cn^{3}[/math]. Решая это разностное уравнение, находим [math] t \approx c\frac{4}{3}n^{3} [/math]

На практике обычно [math]c\lt \lt 1[/math] ( так как матрица [math]Q^{'}[/math] весьма разрежена вследствие дефляциии).

1.7 Информационный граф

Рис. 3. Структура алгоритма "Разделяй и властвуй"

1.8 Ресурс параллелизма алгоритма

Параллелизм достигается за счёт вызова рекурсивных функций dc_eig, вычисляющих собственные значения и собственные вектора матриц [math]T_1[/math] и [math]T_2[/math]. Рекурсивное разделение матрицы приводит к возможности построения структуры в виде двоичного дерева, в каждой вершине которого происходит вычисение функции dc_eig. Таким образом высота алгоритма с использованием распараллеливания, где вычисления для каждого листа дерева в такой структуре происходят независимо, составляет [math]log_2(n)[/math].

1.9 Входные и выходные данные алгоритма

Входные данные: Матрица [math]T[/math] размерностью [math]n \times n[/math]:

[math] T = \begin{bmatrix} a_{1} & b_{1}&&&&& \\ b_{1} & \ddots & \ddots \\ & \ddots & a_{m-1} & b_{m-1} \\ && b_{m-1} & a_{m} & b_{m} \\ &&& b_{m} & a_{m+1} & b_{m+1} \\ &&&& b_{m+1} & \ddots \\ &&&&&& \ddots & b_{n-1} \\ &&&&&& b_{n-1} & a_{n} \\ \end{bmatrix} [/math]

Выходные данные: Собственные значения [math]\alpha_{i}[/math] (всего [math]n[/math]) и собственные векторы [math]\lambda_{i}[/math] (всего [math]n^2[/math]).

1.10 Свойства алгоритма

Возможно ускорение алгоритма посредством метода FMM.

3 Литература

[1] Джеймс Деммель. Вычислительная линейная алгебра. Теория и приложения. изд. Мир, 1/1/2001. — С. 228 - 236.

[2] Divide-and-conquer eigenvalue algorithm [1]

[3] Gr´egoire Pichon, Azzam Haidar, Mathieu Faverge, Jakub Kurzak. Divide and Conquer Symmetric Tridiagonal Eigensolver for Multicore Architectures. 2015. — С. 1 - 11.

[4] C.F. Borges, W.B. Gragg, A parallel divide-and-conquer method for the generalized real symmetric definite tridiagonal eigenproblem, in: L. Reichel, A. Ruttan, R.S. Varga (Eds.), Numerical Linear Algebra, Proc. Conf. in Numerical Linear Algebra and Scientific Computation, Kent, OH, de Gruyter, Berlin, 1993. — С. 11–29

[5] L. Elsner, A. Fasse, E. Langmann. A divide-and-conquer method for the tridiagonal generalized eigenvalue problem. Journal of Computational and Applied Mathematics. 1997. — С. 141 - 148.