Участник:Илья Егоров/Алгоритм k-средних

Алгоритм k-средних (k-means)
Последовательный алгоритм
Последовательная сложность	[math]O(n*k*d)[/math]
Объём входных данных	[math]n*d[/math]
Объём выходных данных	[math]n[/math]

Страница создана группой "Илья Егоров — Евгений Богомазов".

Оба автора в равной мере участвовали в написании, обсуждении и оформлении содержимого статьи. Допустимо считать вклад каждого равным 50%.

1 ЧАСТЬ. Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Алгоритм кластеризации k-средних впервые был предложен в 1950-х годах математиками Гуго Штейнгаузом и Стюартом Ллойдом независимо друг от друга. Наибольшую популярность он получил после работы Маккуина.

Алгоритм позволяет при заданном числе [math]k[/math] построить [math]k[/math] кластеров, расположенных на максимальном расстоянии друг от друга. Таким образом, наибольшей точности результат выполнения алгоритма достигает при полной осведомленности Пользователя о характере кластеризуемых объектов и, как следствие, при обладании максимально корректной информацией о числе кластеров.

В общем случае выбор числа [math]k[/math] может базироваться на любых значимых факторах, в том числе на результатах предшествующих исследований, теоретических соображениях или интуиции.

1.2 Математическое описание алгоритма

Исходные данные:

• Совокупность n d-мерных векторов [math] X = \{x_1 \dots x_n\} , [/math] где [math] x_i = \{x_{i1} \dots x_{id}\} [/math]
• Предполагаемое количество кластеров k

Выходные данные:

• Разбиение X на множество [math] S = \{S_1 \dots S_k \}, \bigcup S_i = X, S_i \cap S_j = \emptyset, i \neq j [/math]
• k центров кластеров [math] \Mu = \{\mu_1 \dots \mu_k \} [/math], где [math] \mu_i = \{\mu_{i1} \dots \mu_{id} \} [/math] такие, что

[math] \begin{cases}\tilde{\mu_i} = \underset{y}{argmin } \sum_{x \in S_i} ||x-y||^2_E \\ \Mu = \underset{\tilde{\Mu}}{argmin } \sum_{i \in k} \sum_{x \in S_i} ||x-\tilde{\mu_i}||^2_E \end{cases} [/math]

Алгоритм:

1) [math] \mu_{i} = random [/math]

2) [math] S_i = \{x \in S~|~\underset{j}{argmin } ||x-\mu_j||_E = i\} i = 1 \dots k [/math]

3) [math] \tilde{\mu_{i}} = E_{x \in S_i}(x) [/math]

4) Если для [math] \forall i: \mu_i = \tilde{\mu_i} [/math] то алгоритм завершен, иначе [math] \mu_i = \tilde{\mu_i} [/math] и перейти на пункт 2)

1.3 Вычислительное ядро алгоритма

Вычислительным ядром алгоритма является второй этап, а точнее нахождение матрицы расстояний между [math]X[/math] и [math]\Mu[/math]. Для d-мерного вектора [math]a:[/math]

[math]||a||=\sqrt{\sum_{i=1\dots d} a_i^2}[/math], поэтому заполнение одной ячейки такой матрицы потребует [math]d[/math] операций умножения, [math]d-1[/math] операций сложения и одну операция вычисления квадратного корня. Но так как эти расстояния используются только для сравнения, а sqrt является монотонно возрастающей функцией, то ее можно не вычислять. Поэтому нахождения матрицы расстояний потребует всего [math]n*k*d[/math] операций умножений и [math]n*k*(d-1)[/math] операций сложений.

1.4 Макроструктура алгоритма

В алгоритме можно выделить следующие макрооперации:

• Вычисление расстояния между векторами,
• Суммирование векторов,
• Поиск минимума в векторе,
• Сравнение векторов,
• Деление вектора на скаляр.

1) На шаге инициализации центроидов в общем случае (случайный выбор элементов) макроопераций не производится. Но так как правило определения количества кластеров k неоднозначно, то для некоторых вариантов макрооперации могут понадобиться. К примеру, существует класс стратегий поиска k, которые базируются на определении центра масс всех объектов, и для которых будут дополнительно выполняться макрооперации "Суммирование векторов" и "Деление вектора на скаляр".

2a) При составлении матрицы расстояний k [math] \cdot [/math] n раз производится макрооперация "Вычисление расстояния между векторами".

2b) При нахождение вектора распределения объектов по кластерам n раз производится макрооперация "Поиск минимума в векторе".

3) При пересчете центроидов n - k раз производится макрооперация "Суммирование векторов" и k раз - "Деление вектора на скаляр".

4) Для проверки критерия останова требуется k раз произвести макрооперацию "Сравнение векторов" для сопоставления обновленных значений центроидов с уже имеющимися.

1.5 Схема реализации последовательного алгоритма

Последовательность шагов алгоритма следующая:

   1) Инициализация центроидов [math]\Mu[/math], [math] iter = 1 [/math], задание максимального количество итераций [math]maxiter[/math]
       
   2a) Нахождение матрицы расстояний [math]dist:[/math]
   
       [math]dist_{ij} = \sum_{l = 1\dots d} (x_{il}-\mu_{jl})^2[/math]
       
   2b) Нахождение вектора распределения объектов по кластерам [math]index: [/math]
   
       [math]index_{i} =   \underset{j}{argmin }~dist_{ij} [/math]
   
   3) Пересчет центроидов [math]\tilde{\Mu}:[/math]
   
       [math]\tilde{\mu_{ij}} = \sum_{l \in S_i} \dfrac{x_{lj}}{|S_i|} [/math], где [math]S_i = \{l~|~l \in 1\dots n, index_l = i\}  [/math]
   
   4) Проверка критерия останова:
   
       Если [math] \exists i: \tilde{\mu_i} \neq \mu_i[/math], [math] iter \lt  maxiter [/math],
   
       то [math] inc(iter), \Mu=\tilde{\Mu},[/math] GOTO 2.а.

1.6 Последовательная сложность алгоритма

   1) Сложность инициализации в общем случае зависит от применяемого метода генерации/получения случайных чисел, но ей можно пренебречь
   
   2a) Вычисление матрицы расстояний требует [math] n*k*d [/math] операций умножения и [math] n*k*(d-1) [/math] операций сложения
   
   2b) Нахождение вектора распределения требует [math] n*(k-1) [/math] операций сравнения
   
   3) Для вычисления [math] \tilde{\Mu} [/math] требуется [math] (n - k + 1) * d [/math] операций сложения и [math] k * d [/math] операций деления
   
   4) Для критерия останова требуется [math] n*d [/math] сравнений

Итого: так как максимальное количество итераций задается в алгоритме заранее и не зависит от входных данных, то количество итераций ограничено константой. Тогда сложность алгоритма:

• [math] O(n*k*d)[/math] операций сложения/вычитания
• [math] O(n*k*d)[/math] операций умножения, [math] O(k*d) [/math] операций деления

1.7 Информационный граф

Рассмотрим вычислительные этапы алгоритма k-means. Это распределение объектов по кластерам и перерасчет центроидов.

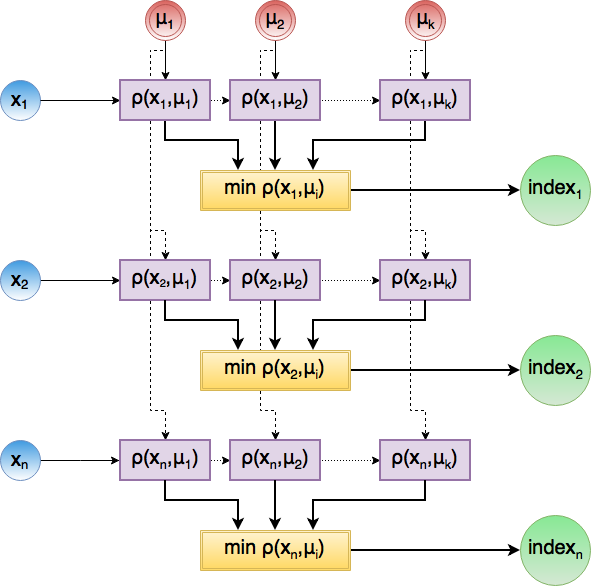
Распределение объектов по кластерам состоит из нахождения матрицы расстояний между [math]X[/math] и [math]\Mu[/math] (этапа 2a)) и нахождения индекса минимального элемента в каждой строке (этап 2b)). Ниже приведен информационный граф данного этапа.

Нахождение вектора индексов распределения по кластерам

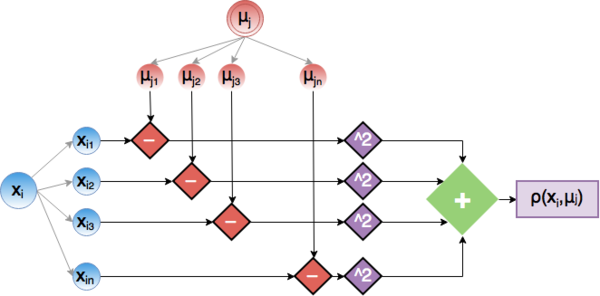
Рассмотрим этап вычисления ячейки [math] dist_{ij} [/math] матрицы более подробно. Он представляет из себя скалярное произведение d-мерных векторов [math] x_i [/math] и [math] \mu_j [/math]. Ниже приведена граф для данной операции.

Операция вычисления расстояния

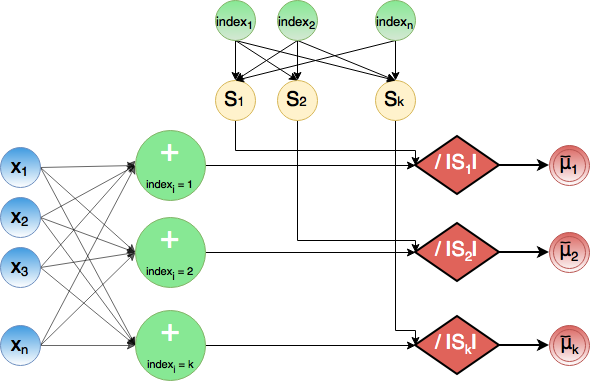
На этапе 3) происходит суммирование всех [math] x_l [/math] с одинаковым значением индекса в промежуточные суммы. Одновременно происходит подсчет количество элементов с фиксированным индексом. Затем происходит деление промежуточных сумм на соответствующее количество элементов в новом кластере, благодаря чему удается получить обновленные центроиды [math] \tilde{\mu}[/math]

Обновление центроидов

1.8 Ресурс параллелизма алгоритма

Для получения общей картины достаточно определить, в том числе и с помощью информационного графа, каким ресурсом параллелизма обладает каждый из этапов алгоритма:

2a) Нахождение каждой ячейки матрицы [math] dist [/math] может происходить полностью независимо, так как они находятся на одном ярусе. При рассмотрении операции вычисления значения конкретной ячейки [math] dist_{ij} [/math] можно заметить, что все операции умножения также независимы между собой, поэтому понадобится всего одно умножение. Конечный результат получается в результате суммирования всех слагаемых и достигается параллельно за [math] \log(d) [/math] бинарных операций сложения при помощи стандартного метода reduction.

2b) Нахождение вектора распределений заключается в нахождении минимального элемента в каждой строке матрицы [math] dist [/math]. При использовании reduction эту операцию можно выполнить за [math] \log(k) [/math] бинарных операций сравнения.

3) В случае, если существует методология быстрого разделения n объектов на k множеств при помощи вектора индексации (косвенной адресации), все [math] \tilde{S_i} [/math] могут быть обработаны параллельно. В рамках каждого отдельного [math] \tilde{S_i} [/math] можно проводить распараллеливание дальше, так как [math] x_{lj} [/math] также не зависят друг от друга. Таким образом, вычисление всех слагаемых для всех [math] \tilde{\mu_{ij}} [/math] может быть выполнено за одно параллельное деление, а нахождение суммы всех этих слагаемых для каждого [math] \tilde{\mu_{ij}} [/math] может быть выполнено за [math] O(log(n)) [/math] в худшем случае (при вхождении почти всех объектов в один кластер).

Если же такой методологии не существует, то узким местом становится процесс распределения на множества согласно вектору [math]index[/math], который можно выполнить за [math] n [/math] операций косвенных адресаций.

4) Все сравнения для критерия останова также независимы между собой и могут быть выполнены за одну операцию сравнения, а финальный результат может быть получен за одну операцию сложения при работе над общей памятью (к примеру, прибавление единицы при несовпадении в общую память и сравнение ее с 0 по завершению) или за [math]\log(k*d)[/math] сложений иначе.

Так как количество итераций ограничено константой, то на сложность оно не влияет. В итоге, параллельная сложность алгоритма k-means такова:

• [math] O(\log(n*d)) [/math] операций сложения
• [math] O(\log(k)) [/math] операций сравнения
• [math] O(1) [/math] операций умножения и деления

1.9 Входные и выходные данные алгоритма

Входные данные: Количество кластеров k, n кластеризуемых элементов

Дополнительные ограничения:

• k — положительное число, т. е. k > 0.
• Для кластеризуемых элементов определена метрика (расстояние между объектами)

Объём входных данных: n [math]\cdot[/math] d + 1 (кластеризуемые объекты в виде векторов и число k)

Выходные данные: Массив, в который записаны принадлежности каждого элемента кластеру (допустим вывод в другой эквивалентной более удобной структуре).

Объём выходных данных: Размер массива равен 2 [math]\cdot[/math] n.

1.10 Свойства алгоритма

Вычислительная мощность

Число действий: [math]n\cdot k\cdot d[/math] умножений

Объем входных данных: [math]n \cdot d + 1[/math]

Вычислительная мощность [math] = \dfrac{n \cdot k \cdot d}{n\cdot d + 1} = k[/math] операций на единицу переданных данных за одну итерацию.

Ограничения алгоритма

Алгоритм эффективно работает только на небольших объемах данных.

Преимущества алгоритма

• Простота использования
• Быстрота использования
• Понятность и прозрачность описания
• Обладает вычислительной устойчивостью
• Предрасположенность к распараллеливанию
• Достаточно популярный, поэтому имеет множество реализаций и вариаций

Недостатки алгоритма

• Нет проверки корректности выбора числа кластеров
• Алгоритм чувствителен к количеству кластеров
• Алгоритм чувствителен к выбору начальных элементов в качестве центроидов
• Алгоритм крайне чувствителен к выбросам по данным
• Медленная работа на больших объемах данных

2 ЧАСТЬ. Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

2.4.2 Масштабируемость реализации

Проведём исследование масштабируемости параллельной реализации алгоритма k-средних. Исследование проводилось на суперкомпьютере "Ломоносов" Суперкомпьютерного комплекса Московского университета.

Набор и границы значений изменяемых параметров запуска реализации алгоритма:

• число процессоров [1 : 16] с увеличением в 2 раза;
• размер данных [100000 : 1600000] с увеличением в 2 раза.

В результате проведённых экспериментов были получены следующие данные:

• Максимальная эффективность в точке достигается при переходе от 1 потока на 8 при минимальном размере данных, она равна [math]87,5%[/math].
• Усредненная максимальная эффективность достигается при переходе с одного потока на два. Среднее время вычислений на всех рассмотренных потока снижается с 16,33 до 11.87 секунд, поэтому формально эффективность [math]= 16.33 / 11.87 / 2 \approx 68,4\%[/math]
• Минимальная эффективность в точке достигается при переходе от 1 потока на 16 при размере данных 800000, она равна [math]11,1\%[/math].
• Усредненная минимальная эффективность наблюдается при переходе с одного на максимальное рассматриваемое в эксперименте число потоков, равное 16. Время вычисления изменяется с 16,33 до 7,6 секунд, поэтому формально эффективность [math] = 16.33 / 7.6 / 16 \approx 14,9\%[/math]

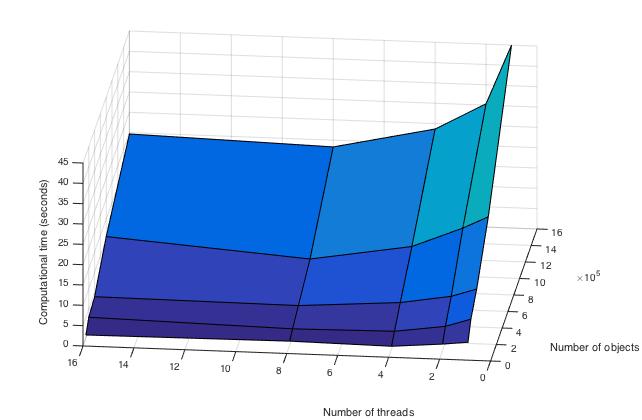
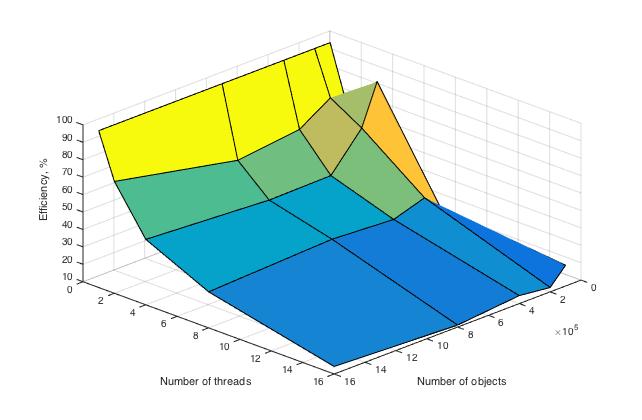
Ниже приведены графики зависимости вычислительного времени алгоритма и его эффективности от изменяемых параметров запуска -- размера данных и числа процессоров:

Параллельная реализация алгоритма k-средних. Изменение вычислительного времени алгоритма в зависимости от числа процессоров и размера исходных данных.

Параллельная реализация алгоритма k-средних. Изменение эффективности алгоритма в зависимости от числа процессоров и размера исходных данных.

Оценка масштабируемости:

По числу процессов - при увеличении числа процессов эффективность уменьшается на всей области рассматриваемых значений, причем темп убывания замедляется с ростом числа процессов.

По размеру задачи - при увеличении размера задачи эффективность вычислений вначале кратковременно возрастает, но затем начинает относительно равномерно убывать на всей рассматриваемой области.

По двум направлениям - при увеличении как размера данных, так и числа процессов по всей рассмотренной области значений эффективность продолжает убывать.

2.7 Существующие реализации алгоритма

2.7.1 Бесплатный доступ

Десктопные программы

• Weka
• Orange

Фреймворки для языков

• Python:
  • scikit-learn
  • SciPy
• C++:
  • MLPACK
  • OpenCV
  • Octave
• C#:
  • Accord.NET
• Java:
  • ELKI
  • Mahout
• Lua
  • Torch

Языки R и Julia содержат алгоритм k-means в базовой реализации.

2.7.2 Платный доступ/лицензия

Существует целый перечень мощных статистических и математических пакетов для разных ОС:

• MATLAB
• Mathematica
• Stata
• SAS
• SAP HANA
• RapidMiner
• ...

3 Литература

[1] Нейский И.М. Классификация и сравнение методов кластеризации http://it-claim.ru/Persons/Neyskiy/Article2_Neiskiy.pdf

[2] https://ru.wikipedia.org/wiki/K-means