Алгоритм Дейкстры: различия между версиями
| [непроверенная версия] | [выверенная версия] |
Ikramov (обсуждение | вклад) |
ASA (обсуждение | вклад) |
||
| Строка 1: | Строка 1: | ||
| + | {{level-a}} | ||
Основные авторы описания: [[Участник:Daryin|А.Н.Дарьин]], [[Участник:VadimVV|Вад.В.Воеводин]] ([[#Описание локальности данных и вычислений|раздел 2.2]]) | Основные авторы описания: [[Участник:Daryin|А.Н.Дарьин]], [[Участник:VadimVV|Вад.В.Воеводин]] ([[#Описание локальности данных и вычислений|раздел 2.2]]) | ||
Версия 17:10, 6 марта 2018
Основные авторы описания: А.Н.Дарьин, Вад.В.Воеводин (раздел 2.2)
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 2.1 Особенности реализации последовательного алгоритма
- 2.2 Локальность данных и вычислений
- 2.3 Возможные способы и особенности параллельной реализации алгоритма
- 2.4 Масштабируемость алгоритма и его реализации
- 2.5 Динамические характеристики и эффективность реализации алгоритма
- 2.6 Выводы для классов архитектур
- 2.7 Существующие реализации алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Алгоритм Дейкстры[1] предназначен для решения задачи поиска кратчайшего пути на графе. Для заданного ориентированного взвешенного графа с неотрицательными весами алгоритм находит кратчайшие расстояния от выделенной вершины-источника до всех остальных вершин графа. Алгоритм Дейкстры (с использованием фибоначчиевой кучи[2]) выполняется за время [math]O(m + n \ln n)[/math] и является асимптотически быстрейшим из известных последовательных алгоритмов для данного класса задач.
1.2 Математическое описание алгоритма
Пусть задан граф [math]G = (V, E)[/math] с весами рёбер [math]f(e)[/math] и выделенной вершиной-источником [math]u[/math]. Обозначим через [math]d(v)[/math] кратчайшее расстояние от источника [math]u[/math] до вершины [math]v[/math].
Пусть уже вычислены все расстояния, не превосходящие некоторого числа [math]r[/math], то есть расстояния до вершин из множества [math]V_r = \{ v \in V \mid d(v) \le r \}[/math]. Пусть
- [math] (v, w) \in \arg\min \{ d(v) + f(e) \mid v \in V, e = (v, w) \in E \}. [/math]
Тогда [math]d(w) = d(v) + f(e)[/math], и [math]v[/math] лежит на кратчайшем пути от [math]u[/math] к [math]w[/math].
Величины [math]d^+(w) = d(v) + f(e)[/math], где [math]v \in V_r[/math], [math]e = (v, w) \in E[/math], называются предполагаемыми расстояниями и являются оценкой сверху для настоящих расстояний: [math]d(w) \le d^+(w)[/math].
Алгоритм Дейкстры на каждом шаге находит вершину с наименьшим предполагаемым расстоянием, помечает её как посещённую и обновляет предполагаемые расстояния для всех концов рёбер, исходящих из неё.
1.3 Вычислительное ядро алгоритма
Основные вычисления связаны с операциями над очередью с приоритетом:
- извлечение минимального элемента (
delete_min); - уменьшение приоритета элемента (
decrease_key).
1.4 Макроструктура алгоритма
Псевдокод алгоритма:
Входные данные:
граф с вершинами V, рёбрами E с весами f(e);
вершина-источник u.
Выходные данные: расстояния d(v) до каждой вершины v ∈ V от вершины u.
Q := new priority queue
for each v ∈ V:
if v = u then d(v) := 0 else d(v) := ∞
Q.insert(v, d(v))
while Q ≠ ∅:
v := Q.delete_min()
for each e = (v, w) ∈ E:
if d(w) > d(v) + f(e):
d(w) := d(v) + f(e)
Q.decrease_key(w, d(w))
1.5 Схема реализации последовательного алгоритма
Конкретная реализация алгоритма Дейкстры определяется выбором используемого алгоритма очереди с приоритетом. В простейшем случае это может быть массив или список, поиск минимума в котором требует просмотра всех вершин. Более эффективным является использование кучи; наилучшую известную оценку сложности имеет вариант с использованием фибоначчиевой кучи[2].
Возможен вариант реализации, когда вершины добавляются в очередь не на этапе инициализации, а в момент первого посещения.
1.6 Последовательная сложность алгоритма
Последовательная сложность алгоритма равна [math]O(C_1 m + C_2n)[/math], где
- [math]C_1[/math] – количество операций уменьшения расстояния до вершины;
- [math]C_2[/math] – количество операций вычисления минимума.
Оригинальный алгоритм Дейкстры использовал в качестве внутренней структуры данных списки, для которых [math]C_1 = O(1)[/math], [math]C_2 = O(n)[/math], так что общая сложность составляла [math]O(n^2)[/math].
При использовании фибоначчиевой кучи[2] время вычисления минимума сокращается до [math]C_2 = O(\ln n)[/math], так что общая сложность равна [math]O(m + n \ln n)[/math], что является асимптотически наилучшим известным результатом для данного класса задач.
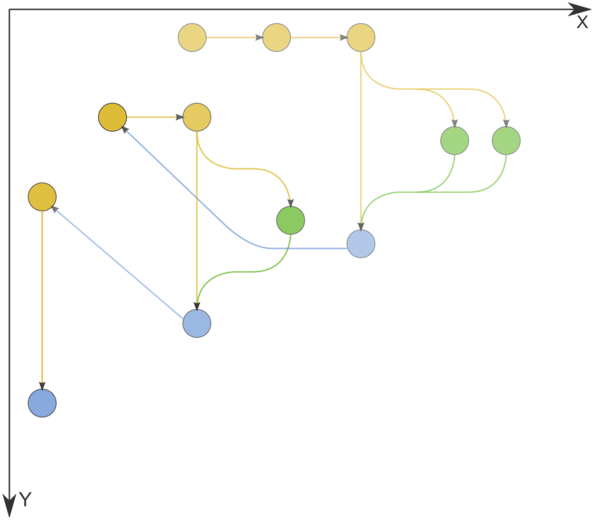
1.7 Информационный граф
Приводится граф алгоритма для базовой реализации алгоритма Дейкстры на списках или массивах.
1.8 Ресурс параллелизма алгоритма
Алгоритм Дейкстры допускает эффективную параллелизацию[3], среднее время работы [math]O(n^{1/3}\ln n)[/math] с объёмом вычислений [math]O(n \ln n + m)[/math].
Алгоритм Δ-шагания может рассматриваться как параллельная версия алгоритма Дейкстры.
1.9 Входные и выходные данные алгоритма
Входные данные: взвешенный граф [math](V, E, W)[/math] ([math]n[/math] вершин [math]v_i[/math] и [math]m[/math] рёбер [math]e_j = (v^{(1)}_{j}, v^{(2)}_{j})[/math] с весами [math]f_j[/math]), вершина-источник [math]u[/math].
Объём входных данных: [math]O(m + n)[/math].
Выходные данные (возможные варианты):
- для каждой вершины [math]v[/math] исходного графа – последнее ребро [math]e^*_v = (w, v)[/math], лежащее на кратчайшем пути от вершины [math]u[/math] к [math]v[/math], или соответствующая вершина [math]w[/math];
- для каждой вершины [math]v[/math] исходного графа – суммарный вес [math]f^*(v)[/math] кратчайшего пути от вершины [math]u[/math] к [math]v[/math].
Объём выходных данных: [math]O(n)[/math].
1.10 Свойства алгоритма
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
2.2 Локальность данных и вычислений
2.2.1 Локальность реализации алгоритма
2.2.1.1 Структура обращений в память и качественная оценка локальности
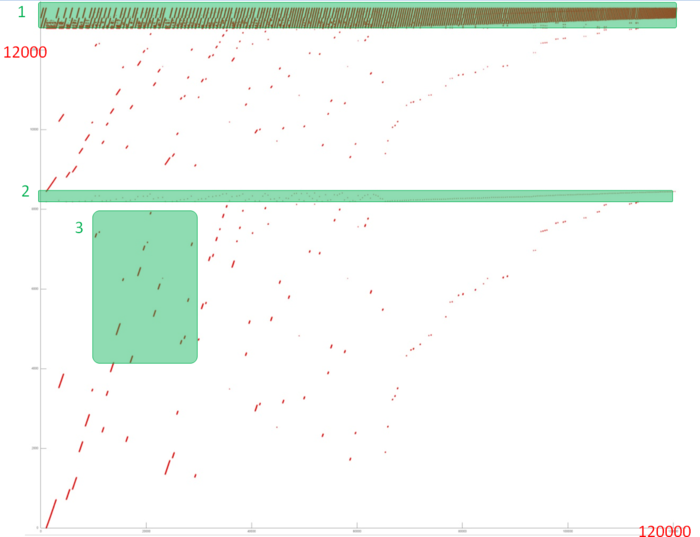
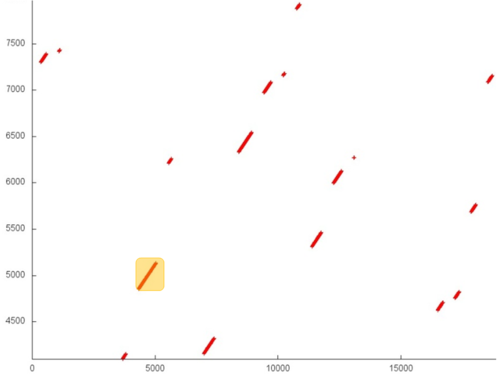
На рис. 1 представлен профиль обращений в память для реализации алгоритма Дейкстры. Первое, что бросается в глаза, – большая разрозненность обращений. В частности, значительные области выше и ниже фрагмента 2 остаются пустыми, при этом сами обращения объединены лишь в небольшие группы. Это говорит о низкой эффективности, поскольку: а) повторные обращения практически отсутствуют либо происходят через значительный промежуток времени; б) расстояния между идущими подряд обращениями может быть очень большим.
Однако при ближайшем рассмотрении может оказаться, что такие участки обладают высокой локальностью и состоят из значительного числа обращений. Более того, на общем профиле есть несколько областей (фрагменты 1 и 2), в которых обращения хорошо локализованы. Необходимо исследовать отдельные участки более подробно.
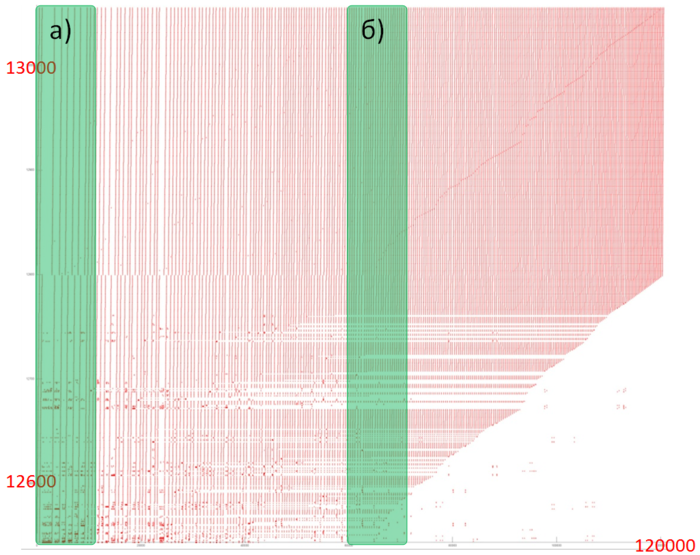
Перейдем к изучению фрагмента 1 (рис. 2), в рамках которого выполняются обращения к двум небольшим массивам. Можно увидеть, что здесь задействованы только примерно 500 элементов, при этом к ним выполняется около 100 тысяч обращений. Весь профиль составляет около 120 тысяч обращений, поэтому получается, что подавляющая их часть выполняется именно к этим элементам.
Поскольку число элементов невелико, локальность в данном случае заведомо будет достаточно высокой, независимо от структуры самого фрагмента. Однако на рис. 3, где представлены два участка из фрагмента 1, можно увидеть, что фрагмент в основном состоит из последовательных переборов, при этом данные зачастую задействованы повторно через не очень большие промежутки. Все это позволяет говорить, что данный фрагмент обладает высокой как пространственной, так и временной локальностью.
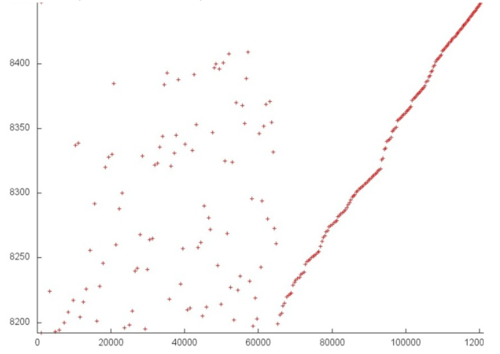
Рассмотрим теперь более подробно фрагмент 2 (рис. 4), в рамках которого выполняются обращения к еще служебному массиву. Здесь профиль состоит из двух этапов. На первом заметен достаточно хаотичный разброс обращений, напоминающий случайный доступ. На втором обращения образуют подобие последовательного перебора. В целом такой профиль характеризуется очень низкой временной локальностью (повторные обращения практически или полностью отсутствуют) и достаточно низкой пространственной локальностью (из-за случайного доступа на первом этапе).
Заметим, что при этом число задействованных элементов здесь больше, чем во фрагменте 1, однако число обращений гораздо меньше.
Далее остаются для рассмотрения два массива (область между фрагментами 1 и 2 и область ниже фрагмента 2). Характер обращений к этим массивам во многом похож, поэтому достаточно изучить более подробно только один из них.
Фрагмент 3 рассмотрен на рис. 5. Этот участок отражаeт достаточно большую область, что не позволяет проанализировать профиль вплоть до отдельных обращений, однако здесь этого и не требуется. Из данного фрагмента видно, что основу профиля составляют участки с последовательным (или с небольшим шагом) перебором, состоящие из небольшого числа элементов – выделенный желтым самый большой участок фрагмента состоит всего из пары сотен обращений. При этом между разными участками расстояние может быть существенным. Все это говорит об очень низкой локальности (как пространственной, так и временной) в случае двух рассматриваемых массивов.
В целом, несмотря на положительный вклад массивов из фрагмента 1, локальность общего профиля должна быть достаточно низкой, вследствие неэффективного использования данных в остальной части профиля.
2.2.1.2 Количественная оценка локальности
Основной фрагмент реализации, на основе которого были получены количественные оценки, приведен здесь (функция Kernel). Условия запуска описаны здесь.
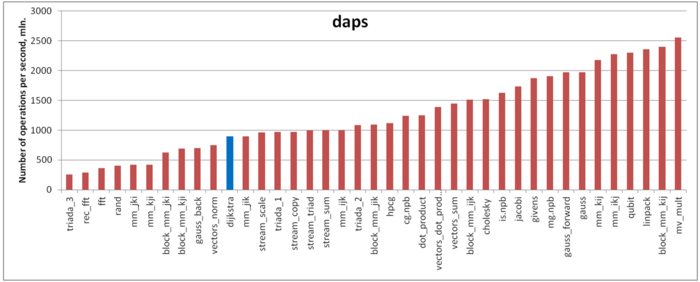
Первая оценка выполняется на основе характеристики daps, которая оценивает число выполненных обращений (чтений и записей) в память в секунду. Данная характеристика является аналогом оценки flops применительно к работе с памятью и является в большей степени оценкой производительности взаимодействия с памятью, чем оценкой локальности. Однако она служит хорошим источником информации, в том числе для сравнения с результатами по следующей характеристике cvg.
На рисунке 6 приведены значения daps для реализаций распространенных алгоритмов, отсортированные по возрастанию (чем больше daps, тем в общем случае выше производительность). Можно увидеть, что производительность работы с памятью достаточно низка. Это неудивительно, поскольку реализации алгоритмов над графами почти всегда обладают низкой эффективностью вследствие нерегулярности доступа к данным, что мы и увидели при анализе профиля обращений.
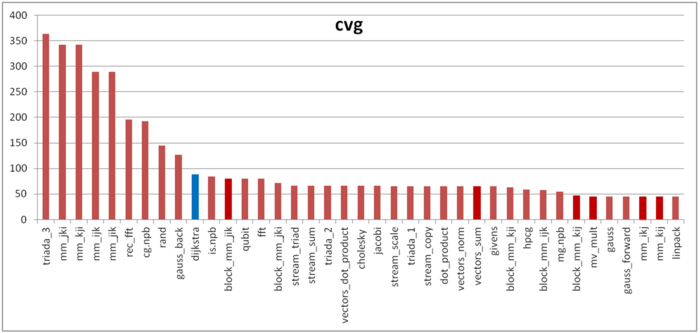
Вторая характеристика – cvg – предназначена для получения более машинно-независимой оценки локальности. Она определяет, насколько часто в программе необходимо подтягивать данные в кэш-память. Соответственно, чем меньше значение cvg, тем реже это нужно делать, тем лучше локальность.
На рисунке 7 приведены значения cvg для того же набора реализаций, отсортированные по убыванию (чем меньше cvg, тем в общем случае выше локальность). Можно увидеть, что в данном случае значение cvg хорошо коррелирует с оценкой производительности и отражает низкую локальность, что соответствует выводам, сделанным при качественной оценке локальности.
2.3 Возможные способы и особенности параллельной реализации алгоритма
2.4 Масштабируемость алгоритма и его реализации
2.4.1 Масштабируемость алгоритма
2.4.2 Масштабируемость реализации алгоритма
Проведём исследование масштабируемости параллельной реализации алгоритма согласно методике. Исследование проводилось на суперкомпьютере "Ломоносов"[4] Суперкомпьютерного комплекса Московского университета. Набор и границы значений изменяемых параметров запуска реализации алгоритма:
- число процессоров [4, 8 : 128] со значениями квадрата целого числа;
- размер графа [16000:64000] с шагом 16000.
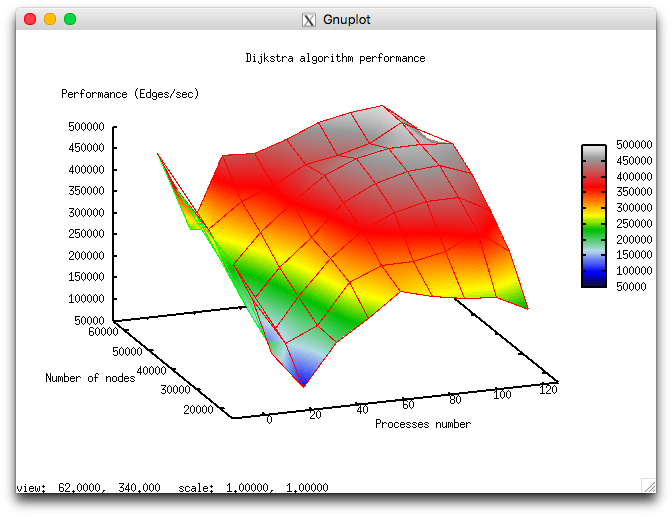
На следующем рисунке приведен график производительности выбранной реализации алгоритма в зависимости от изменяемых параметров запуска.
В силу особенностей параллельной реализации алгоритма производительность в целом достаточно низкая и с ростом числа процессов увеличивается медленно, а при приближении к числу процессов 128 начинает уменьшаться. Это объясняется использованием коллективных операций на каждой итерации алгоритма и тем, что затраты на коммуникационные обмены существенно возрастают с ростом числа использованных процессов. Вычисления на каждом процессе проходят достаточно быстро и потому декомпозиция графа слабо компенсирует эффект от затрат на коммуникационные обмены.
Исследованная параллельная реализация на языке C
2.5 Динамические характеристики и эффективность реализации алгоритма
Для проведения экспериментов использовалась реализация алгоритма Дейкстры. Все результаты получены на суперкомпьютере "Ломоносов". Использовались процессоры Intel Xeon X5570 с пиковой производительностью в 94 Гфлопс, а также компилятор intel 13.1.0. На рисунках показана эффективность реализации алгоритма Дейкстры на 32 процессах.
На графике загрузки процессора видно, что почти все время работы программы уровень загрузки составляет около 50%. Это указывает на равномерную загруженность вычислениями процессоров, при использовании 8 процессов на вычислительный узел и без использования Hyper Threading.
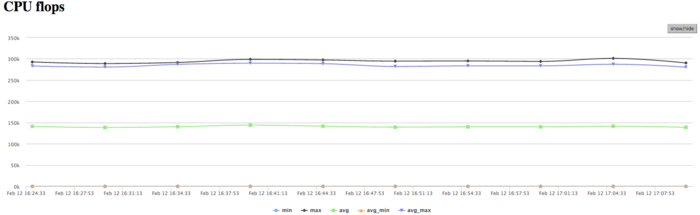
На Рисунке 10 показан график количества операций с плавающей точкой в секунду. На графике видна общая очень низкая производительность вычислений около 250 Kфлопс в пике и около 150 Кфлопс в среднем по всем узлам. Это указывает то, что в программе почти все вычисления производятся с целыми числами.
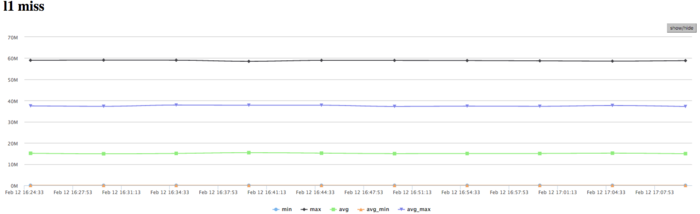
На графике кэш-промахов первого уровня видно, что число промахов очень большое для нескольких ядер и находится на уровне 15 млн/сек (в пике до 60 млн/сек), что указывает на интенсивные вычисления в части процессов. В среднем по всем узлам значения значительно ниже (около 9 млн/сек). Это указывает на неравномерное распределение вычислений.
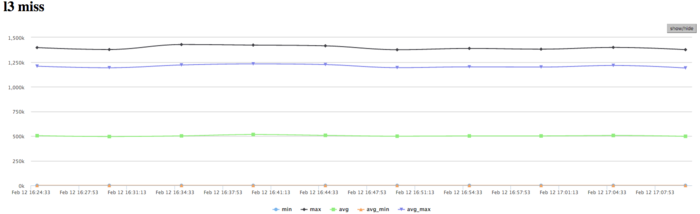
На графике кэш-промахов третьего уровня видно, что число промахов очень невелико и находится на уровне 1,2 млн/сек, однако в среднем по всем узлам значения около 0,5 млн/сек. Соотношение кэш промахов L1|L3 для процессов с высокой производительностью доходит до 60, однако в среднем около 30. Это указывает на очень хорошую локальность вычислений как у части процессов, так и для всех в среднем, и это является признаком высокой производительности.
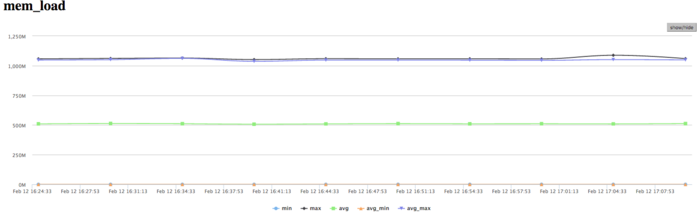
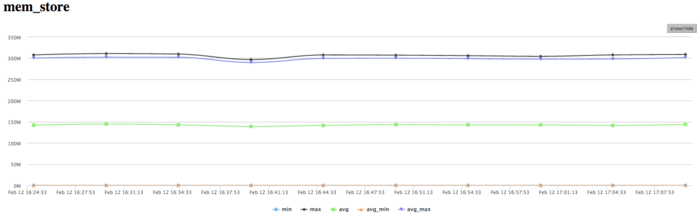
На графике обращений в память видна достаточно типичная картина для таких приложений. Активность чтения достаточно низкая, что в совокупности с низкими значениями кэш-промахов L3 указывает на хорошую локальность. Хорошая локальность приложения также указывает на то, что значение около 1 млн/сек для задачи является результатом высокой производительности вычислений, хотя и присутствует неравномерность между процессами.
На графике записей в память видна похожая картина неравномерности вычислений, при которой одновременно активно выполняют запись только несколько процессов. Это коррелирует с другими графиками выполнения. Стоит отметить достаточно низкое число обращений на запись в память. Это указывает на хорошую организацию вычислений и достаточно эффективную работу с памятью.
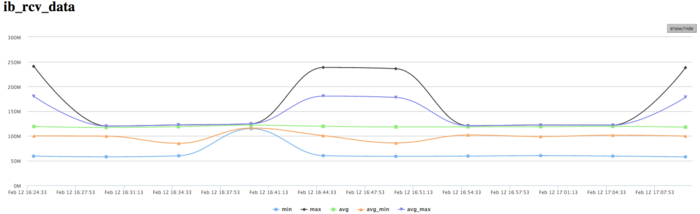
На графике скорости передачи данных по сети Infiniband наблюдается достаточно высокая скорость передачи данных в байтах в секунду. Это говорит о том, что процессы между собой обмениваются интенсивно и вероятно достаточно малыми порциями данных, потому как производительность вычислений высока. Стоит отметить, что скорость передачи отличается между процессами, что указывает на дисбаланс вычислений.
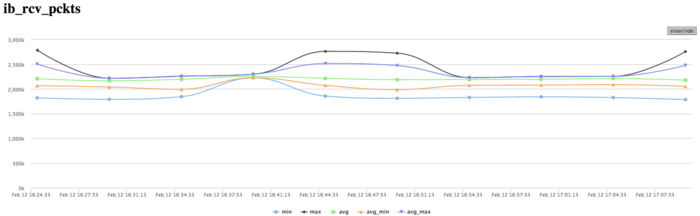
На графике скорости передачи данных в пакетах в секунду наблюдается крайне высокая интенсивность передачи данных. Это говорит о том, что, вероятно, процессы обмениваются не очень существенными объемами данных, но очень интенсивно. Используются коллективные операции на каждом шаге с небольшими порциями данных, что объясняет такую картину. Также наблюдается меньший дизбаланс между процессами, чем наблюдаемый в графиках использования памяти, вычислений и передачи данных в байтах/сек. Это указывает на то, что процессы обмениваются по алгоритму одинаковым числом пакетов, однако получают разные объемы данных и ведут неравномерные вычисления.
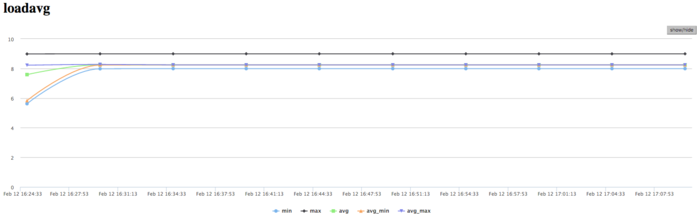
На графике числа процессов, ожидающих вхождения в стадию счета (Loadavg), видно, что на протяжении всей работы программы значение этого параметра постоянно и приблизительно равняется 8. Это свидетельствует о стабильной работе программы с загруженными вычислениями всеми узлами. Это указывает на очень рациональную и статичную загрузку аппаратных ресурсов процессами. И показывает достаточно хорошую эффективность выполняемой реализации. В целом, по данным системного мониторинга работы программы можно сделать вывод о том, что программа работала достаточно эффективно, и стабильно. Использование памяти очень интенсивное, а использование коммуникационной среды крайне интенсивное, при этом объемы передаваемых данных не являются высокими. Это указывает на требовательность к латентности коммуникационной среды алгоритмической части программы. Низкая эффективность связана, судя по всему, с достаточно высоким объемом пересылок на каждом процессе и с интенсивными обменами сообщениями.
2.6 Выводы для классов архитектур
2.7 Существующие реализации алгоритма
- C++: Boost Graph Library (функции
dijkstra_shortest_paths,dijkstra_shortest_paths_no_color_map), сложность [math]O(m + n \ln n)[/math]. - C++, MPI: Parallel Boost Graph Library:
- функция
eager_dijkstra_shortest_paths– непосредственная реализация алгоритма Дейкстры; - функция
crauser_et_al_shortest_paths– реализация алгоритма Дейкстры в виде алгоритма из статьи Краузера и др.[5]
- функция
- Python: NetworkX (функция
single_source_dijkstra). - Python/C++: NetworKit (класс
networkit.graph.Dijkstra).
3 Литература
- ↑ Dijkstra, E W. “A Note on Two Problems in Connexion with Graphs.” Numerische Mathematik 1, no. 1 (December 1959): 269–71. doi:10.1007/BF01386390.
- ↑ 2,0 2,1 2,2 Fredman, Michael L, and Robert Endre Tarjan. “Fibonacci Heaps and Their Uses in Improved Network Optimization Algorithms.” Journal of the ACM 34, no. 3 (July 1987): 596–615. doi:10.1145/28869.28874.
- ↑ Crauser, A, K Mehlhorn, U Meyer, and P Sanders. “A Parallelization of Dijkstra's Shortest Path Algorithm,” Proceedings of Mathematical Foundations of Computer Science / Lecture Notes in Computer Science, 1450:722–31, Berlin, Heidelberg: Springer, 1998. doi:10.1007/BFb0055823.
- ↑ Воеводин Вл., Жуматий С., Соболев С., Антонов А., Брызгалов П., Никитенко Д., Стефанов К., Воеводин Вад. Практика суперкомпьютера «Ломоносов» // Открытые системы, 2012, N 7, С. 36-39.
- ↑ Crauser, A, K Mehlhorn, U Meyer, and P Sanders. “A Parallelization of Dijkstra's Shortest Path Algorithm,” Proceedings of Mathematical Foundations of Computer Science / Lecture Notes in Computer Science, 1450:722–31, Berlin, Heidelberg: Springer, 1998. doi:10.1007/BFb0055823.