Участник:Amirida/Метод «разделяй и властвуй» вычисления собственных значений и векторов симметричной трехдиагональной матрицы

Метод «разделяй и властвуй» вычисления собственных значений и векторов симметричной трехдиагональной матрицы.

Авторы:

Изотова И.А. (619 группа) пункты 1.1, 1.2, 1.5, 1.7, 1.9

Ульянов Г.В. (619 группа) пункты 1.3, 1.4, 1.6, 1.8, 1.10

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

«Разделяй и властвуй» - метод вычисления собственных значений и векторов симметричной трехдиагональной матрицы. В настоящее время это один из самых быстрых методов при вычислении собственных значений и векторов симметричной трехдиагональной матрицы порядка [math]n \gt 25[/math] (точное значение этого порогового порядка зависит от компьютера.) Его численно устойчивая реализация весьма не тривиальна. Хотя впервые метод был предложен еще в 1981 г., "правильный" способ его реализации был найден лишь в 1992 г. Этот способ воплощен LAPACK-программами ssyevd (для плотных матриц) и sstevd (для трехдиагональных матриц). В них стратегия "разделяй-и-влавствуй" используется для матриц порядка, большего чем 25. Для матриц меньшего порядка (или если нужны только собственные значения) происходит автоматический переход к QR-итерации. Однако, из-за высокой сложности, алгоритм пока не вошел в состав ALGLIB.

В наихудшем случае алгоритм «разделяй-и-властвуй» требует [math] O(n^{3})[/math] операций, но константа, на практике оказывается весьма малой. На большой выборке случайных тестовых матриц в среднем затрачивается лишь [math] O(n^{2.3})[/math] операций с плавающей точкой, а для некоторых специальных распределений собственных значений — [math] O(n^{2})[/math] (подробнее в разделе 1.6 Последовательная сложность алгоритма).

1.2 Математическое описание алгоритма

Разделяй

Пусть матрицы [math]T, T_{1}[/math], [math]T_{2}[/math] имеют размерность [math]n \times n[/math], [math]m \times m[/math], [math](n - m) \times (n - m)[/math].

Запишем матрицу [math]T[/math] в следующем виде:

[math] T = \begin{bmatrix} a_{1} & b_{1}&&&&& \\ b_{1} & \ddots & \ddots \\ & \ddots & a_{m-1} & b_{m-1} \\ && b_{m-1} & a_{m} & b_{m} \\ &&& b_{m} & a_{m+1} & b_{m+1} \\ &&&& b_{m+1} & \ddots \\ &&&&&& \ddots & b_{n-1} \\ &&&&&& b_{n-1} & a_{n} \\ \end{bmatrix} = \begin{bmatrix} a_{1} & b_{1} &&&&& \\ b_{1} & \ddots & \ddots \\ & \ddots & a_{m-1} & b_{m-1} \\ && b_{m-1} & a_{m} - b_{m} \\ &&&& a_{m+1} - b_{m} & b_{m+1} \\ &&&& b_{m+1} & \ddots \\ &&&&&& \ddots & b_{n-1} \\ &&&&&& b_{n-1} & a_{n} \\ \end{bmatrix} + [/math]

[math] + \begin{bmatrix} b_{m} & b_{m} \\ b_{m} & b_{m} \\ \end{bmatrix} = \begin{bmatrix} T_{1} & 0 \\ 0 & T_{2} \end{bmatrix} + b_{m} * \begin{bmatrix} 0 \\ \vdots \\ 0 \\ 1 \\ 1 \\ 0 \\ \vdots \\ 0 \end{bmatrix} \begin{bmatrix} 0 , \ldots , 0 , 1 , 1 , 0 \ldots , 0 \end{bmatrix} \equiv \begin{bmatrix} T_{1} & 0 \\ 0 & T_{2}\end{bmatrix} + b_{m}vv^{T} [/math]

Предположим, что нам известны спектральные разложения матриц [math]\hat{T}_{1}[/math] и [math]\hat{T}_{2}[/math], т.е.: [math]\hat{T}_{1} = Q_{1} D_{1} Q_{1}^{T}[/math] и [math]\hat{T}_{2} = Q_{2} D_{2} Q_{2}^{T}[/math].

Властвуй

Установим связь между собственными значениями матрицы [math]T[/math] и собственными значениями матриц [math]T_{1}[/math] и [math]T_{2}[/math]:

[math] T = \begin{bmatrix} T_{1} & 0 \\ 0 & T_{2}\end{bmatrix} + b_{m}vv^{T} = \begin{bmatrix} Q_{1} \Lambda_{1} Q_{1}^{T} & 0 \\ 0 & Q_{2} L_{2} Q_{2}^{T}\end{bmatrix} + b_{m}vv^{T} = \begin{bmatrix} Q_{1} & 0 \\ 0 & Q_{2}\end{bmatrix}(\begin{bmatrix} \Lambda_{1} & \\ & \Lambda_{2}\end{bmatrix} + b_{m}vv^{T})\begin{bmatrix} Q_{1}^{T} & 0 \\ 0 & Q_{2}^{T}\end{bmatrix} [/math],

где [math] u = \begin{bmatrix} Q_{1}^{T} & 0 \\ 0 & Q_{2}^{T}\end{bmatrix}v [/math] - матрица, в первой строке которой находятся элементы последнего столбца матрицы [math] Q_{1}^{T}[/math], а во второй - элементы первого столбца матрицы [math] Q_{2}^{T}[/math], так как [math]v = \begin{bmatrix} 0 , \ldots , 0 , 1 , 1 , 0 \ldots , 0 \end{bmatrix}^T[/math]. Следовательно, [math]T[/math] имеет такие же собственные значения, что и подобная ей матрица [math]D + \rho uu^{T}[/math], где [math]D = \begin{bmatrix} L_{1} & 0 \\ 0 & L_{2}\end{bmatrix}[/math] - диагональная матрица, [math]\rho = b_{m}[/math] - число, а [math]u[/math] - вектор. В дальнейшем предполагаем, не ограничивая общности, что диагональные элементы [math]d_{1}, \ldots, d_{n}[/math] матрицы [math]D[/math] упорядочены по не возрастанию: [math]d_{n} \lt = \ldots \lt =d_{1}[/math].

Для того, чтобы найти собственные значения матрицы [math]D + \rho uu^{T}[/math], потребуется вычислить её характеристический многочлен, считая пока матрицу [math]D - \lambda I[/math] невырожденной. Тогда получаем [math]det(D + \rho uu^{T} - \lambda I) = det((D - \lambda I)(I + \rho (D- \lambda I)^{-1} uu^{T}))[/math].

Так как [math]D - \lambda I[/math] невырожденная, [math]det(I + \rho (D - \lambda I)^{-1}uu^{T}) = 0[/math] тогда и только тогда, когда [math]\lambda[/math] - является собственным значением. Можем заметить, что матрица [math]I + \rho (D - \lambda I)^{-1}uu^{T}[/math] получается из единичной путём добавления матрицы ранга 1. Определитель такой матрицы не сложно вычислить.

 Лемма 1. Справедливо равенство [math]det(I + xy^{T}) = 1 + y^{T}x[/math], где [math]x[/math] и [math]y[/math] - векторы.

Следовательно, получаем [math]det(I + \rho (D - \lambda I)^{-1}uu^{T}) = 1 + \rho u^{T}(D - \lambda I)^{-1}u[/math] [math] = 1 + \rho \sum_{i=1, n} \frac{u_{i}^{2}} {d_{i}-\lambda} \equiv f(\lambda)[/math] ,

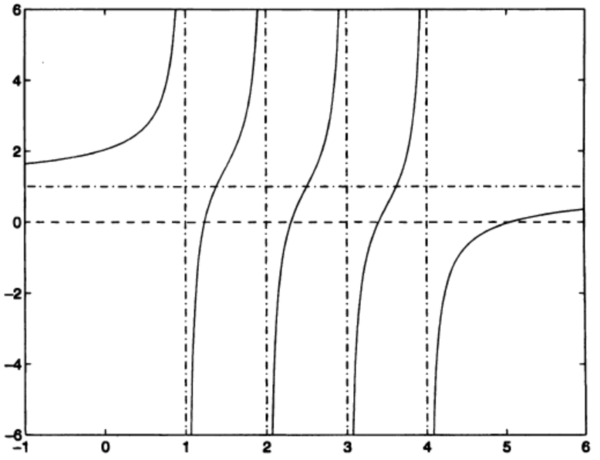
т.е. собственные значения матрицы [math]T[/math] являются корнями так называемого векового уравнения [math]f(\lambda) = 0[/math]. Если все числа [math]d_{i}[/math] различны между собой и все [math]u_{i} \lt \gt 0[/math] (случай общего положения), то [math]f(\lambda)[/math] имеет график типа, который показан на рис.1(где [math]n = 4[/math] и [math]\rho \gt 0[/math]).

Рис. 1. График функции [math] f(\lambda) = 1 + \frac{0.5}{1 - \lambda} + \frac{0.5}{2 - \lambda} + \frac{0.5}{3 - \lambda} + \frac{0.5}{4 - \lambda}[/math]

По Рис.1 можно заметить, что прямая [math]y = 1[/math] является горизонтальной асимптотой для данного графика, а прямые [math]\lambda = d_{i}[/math] есть вертикальные асимптоты. Так как [math]f^{'}(\lambda) = \rho \sum_{i=1, n} \frac{u_{i}^{2}} {(d_{i}-\lambda)^{2}}\gt 0 [/math], функция возрастает всюду, кроме точек [math]\lambda = d_{i}[/math]. Из этого следует, что корни функции разделяются числами [math]d_{i}[/math] и ещё один корень находится справа от точки [math]d_{1}[/math] (на рис. 1 [math]d_{1} = 4[/math]). (При [math]\rho\lt 0[/math] функция [math]f(\lambda)[/math] всюду убывает и соответствующий корень будет находиться слева от точки [math]d_{n}[/math]). Для функции [math]f(\lambda)[/math], которая является монотонной и гладкой на каждом из интервалов [math](d_{i+1},d_{i})[/math], можно найти вариант метода Ньютона, который будет быстро и монотонно сходиться к каждому из корней, при условии, что начальная точка взята в [math](d_{i+1},d_{i})[/math]. Нам достаточно знать тот факт, что на практике метод сходится к каждому собственному значению за строго ограниченное число шагов. Поскольку вычисление [math]f(\lambda)[/math] и [math]f^{'}(\lambda)[/math] стоит [math]O(n)[/math] флопов, для вычисления одного собственного значения достаточно [math]O(n)[/math] флопов, следовательно для вычисления всех [math]n[/math] собственных значений матрицы [math]D + \rho uu^{T}[/math] потребуется [math]O(n^{2})[/math] флопов. Для собственных векторов матрицы [math]D + \rho uu^{T}[/math] мы легко можем получить явные выражения.

 Лемма 2. Если [math]\alpha[/math] - собственное значение матрицы [math]D + \rho uu^{T}[/math], то соответствующий вектор равен [math](D - \alpha I)^{-1}u[/math]. Поскольку матрица [math]D - \alpha I[/math] диагональная, для вычисления такого вектора достаточно [math]O(n)[/math] флопов.

Доказательство:

[math](D + \rho uu^{T})[(D - \alpha I)^{-1}u] = (D - \alpha I + \alpha I + \rho uu^{T})(D - \alpha I)^{-1}u = u + \alpha (D - \alpha I)^{-1}u + u[\rho u^{T}(D - \alpha I)^{-1}u]= [/math]

[math] = u + \alpha(D - \alpha I)^{-1}u - u = \alpha [(D - \alpha I)^{-1}u][/math],

поскольку

[math] \rho u^{T}(D - \alpha I)^{-1}u + 1 = f(\alpha) = 0 [/math].

Что и требовалось доказать.

Получается, что для вычисления по этой простой формуле всех [math]n[/math] собственных векторов потребуется [math]O(n^{2})[/math] флопов. К сожалению, данная формула не обеспечивает нам численной устойчивости, так как для двух очень близких значений [math]\alpha_{i}[/math] может давать неортогональные приближенные собственные векторы [math]u_{i}[/math]. Учёным потребовалось целое десятилетие для того, чтобы найти устойчивую альтернативу исходному описанию алгоритма. Подробнее детали будут обсуждаться ниже в данном разделе.

1.3 Вычислительное ядро алгоритма

Вычислительным ядром последовательной схемы решения будет являться вычисление матрицы [math]Q[/math] собственных векторов при помощи умножения матрицы [math]Q = \begin{bmatrix} Q_{1} & 0 \\ 0 & Q_{2}\end{bmatrix}[/math] на матрицу [math]Q^{'}[/math]. Эта операция имеет сложность [math]cn^{3}[/math] о чём будет говориться ниже, в разделе 1.6 Последовательная сложность алгоритма .

Данной операции предшествует вычисление собственных значений и векторов матрицы [math] D + \rho uu^{T}[/math].

1.4 Макроструктура алгоритма

Дефляция

До сих пор полагалось, что все [math]d_{i}[/math] различны и все [math]u_{i}[/math] отличны от нуля. Если это не так, вековое уравнение [math]f(\lambda)=0[/math] имеет [math]k[/math] вертикальных асимптот, где [math]k\lt n[/math], а потому [math]k[/math] корней. Однако оказывается, что остальные [math]n - k[/math] собственных значений могут быть определены без каких-либо усилий: если [math]d_{i}=d_{i+1}[/math] или [math]u_{i}=0[/math], то легко показать, что [math]d_{i}[/math] является собственным значением и для матрицы [math]D + \rho uu^{T}[/math]. В такой ситуации мы говорим о дефляции. На практике выбирается некоторое пороговое значение и дефляция для числа [math]d_{i}[/math] регистрируется, если в смысле этого порога [math]d_{i}[/math] достаточно близко к [math]d_{i+1}[/math] либо [math]u_{i}[/math] достаточно мало.

Основной выигрыш от использования дефляции состоит не в том, что убыстряется решение векового уравнения - этот этап в любом случае стоит лишь [math]O(n^{2})[/math] операций. Выигрыш заключается в ускорении матричного умножения на последнем шаге алгоритма. Действительно, если [math]u_{i}=0[/math], то соответствующий собственный вектор есть i-й столбец [math]e_{i}[/math] единичной матрицы. Это означает, что [math]e_{i}[/math] является i-м столбцом в матрице [math]Q_{'}[/math], поэтому при формировании матрицы [math]Q[/math] посредством левого умножения [math]Q_{1}[/math] на [math]Q_{2}[/math] вычисление i-го столбца не требует никаких затрат. Аналогичное упрощение имеет место в случае [math]d_{i} = d_{i+1}[/math]. При дефляции многих собственных значений устраняется большая часть работы, связанной с матричным умножением.

Метод Ньютона

Далее пойдет речь о решении векового уравнения, которое является одной из основных частей алгоритма.

Предположим, что некоторое [math]u_{i}[/math], хотя и мало, все же недостаточно мало для того, чтобы была зарегистрирована дефляция. В этом случае применение метода Ньютона к решению векового уравнения встречается с затруднениями. Вспомним, что пересчет приближённого решения [math]u_{j}[/math] уравнения [math]f(\lambda) = 0[/math] в методе Ньютона основан на следующих положениях:

1. Вблизи точки [math]\lambda = \lambda_{j}[/math] функция [math]f(\lambda)[/math] аппроксимируется линейной функцией [math]l(\lambda)[/math]; график есть прямая линия, касающаяся графика функции [math]f(\lambda)[/math] при [math]\lambda = \lambda_{j}[/math].

2. В качестве [math]\lambda_{j+1}[/math] берётся нуль этого линейного приближения, т.е. [math]l(\lambda_{j+1})=0[/math].

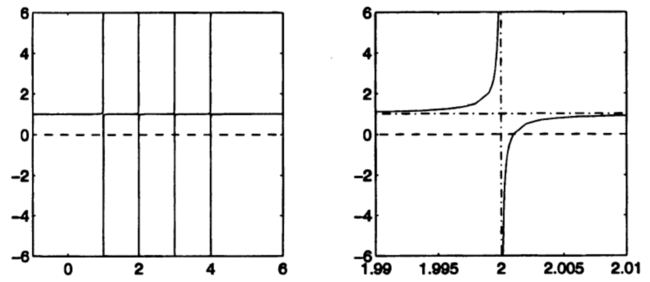
Функция, показанная на рис.1, не доставляет видимых трудностей методу Ньютона, поскольку вблизи каждого своего нуля [math]f(\lambda)[/math] достаточно хорошо аппроксимируется линейными функциями. Однако рассмотрим график функции на рис. 2. Она получена из функции на рис. 1 заменой значения .5 для [math]u_{i}^{2}[/math] на .001. Это новое значение недостаточно мало для того, чтобы вызвать дефляцию. График функции в левой части рис.2 визуально не отличим от её вертикальных и горизонтальных асимптот, поэтому в правой части укрупненно воспроизведён фрагмент графика, прилегающий к вертикальной асимптоте [math]\lambda = 2[/math]. Видно, что график слишком быстро "выполняет поворот" и для большей части значений [math]\lambda[/math] почти горизонтален. Поэтому, применяя метод Ньютона почти к любому начальному приближению [math]\lambda_{0}[/math], мы получаем линейное приближение [math]l(\lambda)[/math] с почти горизонтальным графиком и малым положительным угловым коэффициентом. В результате [math]\lambda_{1}[/math] является отрицательным числом, огромным по абсолютной величине, которое совершенно бесполезно в качестве приближения к истинному корню.

Рис. 2. График функции [math] f(\lambda) = 1 + \frac{10^{-3}}{1 - \lambda} + \frac{10^{-3}}{2 - \lambda} + \frac{10^{-3}}{3 - \lambda} + \frac{10^{-3}}{4 - \lambda}[/math]

Чтобы найти выход из этого положения, можно модифицировать метод Ньютона следующим образом: раз [math]f(\lambda)[/math] нельзя хорошо приблизить линейной функцией [math]l(\lambda)[/math], попробуем взять в качестве приближения какую-нибудь другую простую функцию [math]h(\lambda)[/math]. Нет ничего особого именно в прямых линиях: для метода Ньютона вместо [math]l(\lambda)[/math] можно взять любое приближение [math]h(\lambda)[/math], значения и нули которого легко вычисляются. Функция [math]f(\lambda)[/math] имеет полюсы в точках [math]d_{i}[/math] и [math]d_{i+1}[/math], которые определяют её поведение в соответствующих окрестностях. Поэтому при поиске корня в интервале [math](d_{i+1}, d_{i})[/math] естественно выбрать функцию [math]h(\lambda)[/math], также имеющую эти полюсы, т.е. функцию вида [math]h(\lambda)= \frac{c_{1}}{d_{i}-\lambda} + \frac{c_{2}}{d_{i+1}-\lambda} + c_{3}[/math]

Константы [math]c_{1},c_{2}[/math] и [math]c_{3}[/math] обеспечивающие, что [math]h(\lambda)[/math] есть приближение к [math]f(\lambda)[/math], можно выбрать несколькими способами. Отметим, что если [math]c_{1},c_{2}[/math] и [math]c_{3}[/math] уже известны, то уравнение [math]h(\lambda)=0[/math] легко решается относительно [math]\lambda[/math], поскольку сводится к эквивалентному квадратному уравнению [math]c_{1}(d_{i+1}-\lambda)+c_{2}(d_{i}-\lambda)+c_{3}(d_{i}-\lambda)(d_{i+1}-\lambda)=0[/math]

Пусть [math]\lambda_{j}[/math] - приближённое значение корня. определим [math]c_{1},c_{2}[/math] и [math]c_{3}[/math] так, чтобы [math]\frac{c_{1}}{d_{i}-\lambda} + \frac{c_{2}}{d_{i+1}-\lambda} + c_{3} = h(\lambda) \approx f(\lambda) = 1 + \rho \sum_{k=1, n} \frac{u_{k}^{2}} {d_{k}-\lambda} [/math] для [math]\lambda[/math] в окрестности [math]\lambda_{j}[/math]. Заметим, что [math]f(\lambda) = 1 + \rho \sum_{k=1, i} \frac{u_{k}^{2}} {d_{k}-\lambda} + \rho \sum_{k=i+1, n} \frac{u_{k}^{2}} {d_{k}-\lambda} \equiv 1 + \psi_{1}(\lambda) + \psi_{2}(\lambda)[/math].

Если [math]\lambda \in (d_{i+1},d_{i})[/math], то [math]\psi_{1}(\lambda)[/math] есть сумма положительных слагаемых, а [math]\psi_{2}(\lambda)[/math] - сумма отрицательных. Поэтому и [math]\psi_{1}(\lambda)[/math], и [math]\psi_{2}(\lambda)[/math] могут быть вычислены с высокой точностью; однако при их сложении вполне вероятно взаимное уничтожение верных разрядов и потеря относительной точности в сумме. Возьмем числа [math]c_{1}[/math] и [math]\hat{c_{1}}[/math], такие, что функция [math]h_{1}(\lambda) \equiv \hat{c_{1}} + \frac{c_{1}}{d_{i}-\lambda}[/math] удовлетворяет условиям [math]h_{1}(\lambda_{j}) = \psi_{1}(\lambda_{j})[/math] и [math]h_{1}^{'}(\lambda_{j})=\psi_{1}^{'}(\lambda_{j})[/math] (*)

Это означает, что гипербола, являющаяся графиком функции [math]h_{1}(\lambda)[/math], касается графика функции [math]\psi_{i}(\lambda)[/math] при [math]\lambda = \lambda_{j}[/math]. Два условия в (*) - это обычные условия метода Ньютона, за исключением того, что вместо прямой в качестве приближения используется гипербола. Легко проверить, что [math]c_{1}=\psi_{1}^{'}(\lambda_{j})(d_{i} - \lambda_{j})^{2}[/math] и [math]\hat{c_{1}}=\psi_{1}(\lambda_{j}) - \psi_{1}^{'}(\lambda_{j})(d_{i} - \lambda_{j})[/math].

Подобным же образом выбираем [math]c_{2}[/math] и [math]\hat{c_{2}}[/math] так, чтобы функция [math]h_{2}(\lambda) \equiv \hat{c_{2}} + \frac{c_{2}}{d_{i+1}-\lambda}[/math] удовлетворяла условиям [math]h_{2}(\lambda_{j}) = \psi_{2}(\lambda_{j})[/math] и [math]h_{2}^{'}(\lambda_{j})=\psi_{2}^{'}(\lambda_{j})[/math]

Наконец, полагаем [math]h(\lambda) = 1 + h_{1}(\lambda) + h_{2}(\lambda) = (1 + \hat{c_{1}} + \hat{c_{2}} + \frac{c_{1}}{d_{i}-\lambda} + \frac{c_{2}}{d_{i+1}-\lambda} \equiv c_{3} + \frac{c_{1}}{d_{i}-\lambda} + \frac{c_{2}}{d_{i+1}-\lambda}[/math].

Как только из векового уравнения найдены собственные значения [math]\alpha_{i}[/math] матрицы [math]D + \rho uu^{T}[/math], можно вычислить собственные векторы, пользуясь просто формулой [math](D - \alpha_{i})^{-1}u[/math] и из Леммы 2.К сожалению, вычисления по этой формуле могут быть неустойчивы. Так будет, в частности, когда собственные значения [math]\alpha_{i}[/math], [math]\alpha_{i+1}[/math] очень близки. Интуитивно проблема состоит в том, что выражения [math](D - \alpha_{i})^{-1}u[/math] и [math](D - \alpha_{i+1})^{-1}u[/math] "очень похожи", в то время как требуется получить ортогональные собственные векторы. Более точно, если [math]\alpha_{i}[/math] и [math]\alpha_{i+1}[/math] очень близки, оба близки к находящемуся между ними числу [math]d_{i}[/math]. Поэтому имеет место заметная потеря верных знаков при вычислении [math]d_{i} - \alpha_{i+1}[/math] или [math]\alpha_{i+1} - d_{i}[/math], либо при решении векового уравнения методом Ньютона. В любом из этих случаев [math]d_{i} - \alpha_{i}[/math] и [math]\alpha_{i+1} - d_{i}[/math] могут содержать большие относительные ошибки, вследствие чего вычисленные собственные векторы [math](D - \alpha_{i})^{-1}u[/math] и [math](D - \alpha_{i+1})^{-1}u[/math] и очень неточны, и далеки от ортогональности.

1.5 Схема реализации последовательного алгоритма

Рассмотри реализацию метода "разделяй и властвуй" в виде алгоритма:

proc dc_eig [math](T, Q, \Lambda) ... [/math]по входной матрице [math]T[/math] вычисляются выходные матрицы [math]Q[/math] и [math]\Lambda[/math], такие, что [math]T = Q\Lambda Q^{T}[/math]
    Если матрица [math]T[/math] имеет размерность [math]1 \times 1[/math]
        присвоить выходным параметрам значения [math]Q = 1, \Lambda = T[/math]
    иначе
        [math]T[/math] в виде [math] T = \begin{bmatrix} T_{1} & 0 \\ 0 & T_{2}\end{bmatrix} + b_{m}vv^{T} [/math]
        call dc_eig[math](T_{1},Q_{1},\Lambda_{1})[/math]
        call dc_eig[math](T_{2},Q_{2},\Lambda_{2})[/math]
        [math]D+\rho uu^{T}[/math] по [math] \Lambda_{1},\Lambda_{2}, Q_{1}, Q_{2}[/math]
        Найти матрицу собственных значений [math]\Lambda[/math]
        Найти матрицу собственных векторов [math]Q^{'}[/math] для матрицы [math]D+\rho uu^{T}[/math]
        Построить матрицу собственных векторов [math]Q[/math] для матрицы [math]T[/math] : [math] Q = \begin{bmatrix} Q_{1} & 0 \\ 0 & 
Q_{2}\end{bmatrix}* Q^{'} [/math]
        Присвоить выходным параметрам значения [math]Q[/math] и [math]\Lambda[/math]
 endif

1.6 Последовательная сложность алгоритма

Пусть [math]t(n)[/math] - число флопов при обработке матрицы размера [math]n \times n[/math] процедурой dc_eig. Тогда

[math]t(n) = 2t(n/2)[/math] два рекурсивных обращения к dc_eig[math](T_{i},Q_{i},\Lambda_{i})[/math]

[math]+O(n^{2})[/math] вычисление собственных значений матрицы [math]D+\rho uu^{T}[/math]

[math]+O(n^{2})[/math] вычисление собственных векторов матрицы [math]D+\rho uu^{T}[/math]

[math]+c*n^{3}[/math] вычисление матрицы [math]Q = \begin{bmatrix} Q_{1} & 0 \\ 0 & Q_{2}\end{bmatrix}*Q^{'}[/math]

Если [math] Q_{1}, Q_{2}[/math] и [math]Q^{'}[/math] рассматриваются как плотные матрицы и используется стандартный алгоритм матричного умножения, то константа [math] c [/math] в последней строке равна 1. Таким образом, именно это умножение составляет наиболее трудоёмкую часть алгоритма в целом. Игнорируя члены порядка [math]n^{2}[/math], получаем [math]t(n) = 2t(n/2) + cn^{3}[/math]. Решая это разностное уравнение, находим [math] t \approx c\frac{4}{3}n^{3} [/math]

На практике обычно [math]c\lt \lt 1[/math] ( так как матрица [math]Q^{'}[/math] весьма разрежена вследствие дефляциии).

1.7 Информационный граф

Рис. 3. Структура алгоритма "Разделяй и властвуй"

1.9 Входные и выходные данные алгоритма

Входные данные: Матрица [math]T[/math] размерностью [math]n \times n[/math]:

[math] T = \begin{bmatrix} a_{1} & b_{1}&&&&& \\ b_{1} & \ddots & \ddots \\ & \ddots & a_{m-1} & b_{m-1} \\ && b_{m-1} & a_{m} & b_{m} \\ &&& b_{m} & a_{m+1} & b_{m+1} \\ &&&& b_{m+1} & \ddots \\ &&&&&& \ddots & b_{n-1} \\ &&&&&& b_{n-1} & a_{n} \\ \end{bmatrix} [/math]

Выходные данные: Собственные значения [math]\alpha_{i}[/math] (всего [math]n[/math]) и собственные векторы [math]\lambda_{i}[/math] (всего [math]n^2[/math]).

1.10 Свойства алгоритма

Возможно ускорение алгоритма посредством метода FMM.

3 Литература

[1] Джеймс Деммель. Вычислительная линейная алгебра. Теория и приложения. изд. Мир, 1/1/2001. — С. 228 - 236.

[2] Divide-and-conquer eigenvalue algorithm [1]

[3] Gr´egoire Pichon, Azzam Haidar, Mathieu Faverge, Jakub Kurzak. Divide and Conquer Symmetric Tridiagonal Eigensolver for Multicore Architectures. 2015. — С. 1 - 11.

[4] C.F. Borges, W.B. Gragg, A parallel divide-and-conquer method for the generalized real symmetric definite tridiagonal eigenproblem, in: L. Reichel, A. Ruttan, R.S. Varga (Eds.), Numerical Linear Algebra, Proc. Conf. in Numerical Linear Algebra and Scientific Computation, Kent, OH, de Gruyter, Berlin, 1993. — С. 11–29

[5] L. Elsner, A. Fasse, E. Langmann. A divide-and-conquer method for the tridiagonal generalized eigenvalue problem. Journal of Computational and Applied Mathematics. 1997. — С. 141 - 148.