Авторы описания: Готман М.Л., Лукашкина Ю.Н.

Содержание

1 ЧАСТЬ. Свойства и структура алгоритмов
2 ЧАСТЬ. Программная реализация алгоритма
3 Литература

1 ЧАСТЬ. Свойства и структура алгоритмов

1.1 Общее описание алгоритма

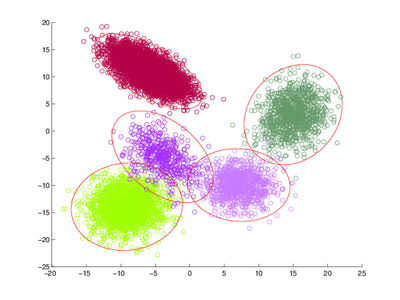
Задача кластеризации — это задача разбиения заданной входной выборки объектов на непересекающиеся подмножества, называемые кластерами, так, чтобы каждый кластер состоял из схожих объектов, а объекты разных кластеров существенно отличались.

Для решения этой задачи можно использовать, например, метод максимизации ожидания, также известный как EM-алгоритм (англ. expectation-maximization) ^[1]. В таком случае делается предположение, что входные данные — смесь многомерных нормальных распределений, соотвественно отдельный кластер — это одна компонента смеси. Предполагается, что количество кластеров является входным параметром алгоритма (существуют модификации EM-алгоритма, которые автоматически находят число кластеров, но они не рассматриваются в данной статье). Результат работы EM-алгоритма — веса кластеров и найденные параметры нормальных распределений для каждого кластера: вектора математических ожиданий и матрицы ковариации.

Алгоритм EM кластеризации основан на итеративном выполнении двух последовательных шагов: E-шага и M-шага. На E-шаге вычисляются вспомогательные (скрытые) переменные, которые характеризуют апостериорную вероятность того, что определенный обучающий объект получен из фиксированной компоненты смеси. На M-шаге с помощью вычисленных скрытых переменных производится обновление параметров смеси: по определённым формулам пересчитываются веса кластеров, их математические ожидания и матрицы ковариаций.

Стоит отметить, что на работу EM-алгоритма значительно влияет начальное приближение его параметров. При неудачной инициализации алгоритм может не сойтись или сойтись в локальный экстремум.

В данной статье рассматривается частный случай EM-алгоритма, который работает с двумерными входными данными.

Пример работы EM-алгоритма для 5ти кластеров.

1.2 Математическое описание алгоритма

Рассматривается смесь многомерных нормальных распределений [math]p_j(x) = N(x;\mu_j, \Sigma_j) = \frac1{(2\pi)^{d/2}\sqrt{|\Sigma_j|}} \exp \biggl(-\frac{1}{2}(x - \mu_j) \Sigma_j^{-1} (x - \mu_j)^T\biggr) [/math] с весами [math]w_j[/math]: [math]p(x)=\sum_{j=1}^kw_jp_j(x), \sum_{j=1}^kw_j =1, w_j \ge 0[/math].

На вход алгоритму подаются [math]m [/math] объектов, каждый из которых имеет [math]d[/math] признаков, в виде матрицы объектов-признаков [math]X \in \R^{m \times d}[/math] и [math]k[/math] — количество кластеров.

Алгоритм кластеризации, основанный на максимизации правдоподобия, итеративно выполняет два шага: E-шаг и M-шаг. Идея алгоритма заключается в введении матрицы скрытых переменных [math]G[/math], где [math]g_{ij} \equiv P(\theta_j |x_i)[/math] обозначает вероятность принадлежности [math]i[/math]-го объекта [math]j[/math]-му кластеру.

На Е-шаге вычисляется ожидаемое значение скрытых переменных, на М-шаге выполняется максимизация логарифма полного правдоподобия, результатом которой являются новые значения параметров модели.

На выходе получаем набор параметров модели для каждого кластера [math]\Theta = (w_1,...,w_k;\;\mu_1,...,\mu_k;\;\Sigma_1,...,\Sigma_k)[/math], где [math]w_j[/math] — вес [math]j[/math]-го кластера в смеси нормальных распределений, [math]\mu_j[/math] — математическое ожидание [math]j[/math]-ой компоненты смеси, [math]\Sigma_j[/math] — матрица ковариации [math]j[/math]-ой компоненты смеси.

E-шаг:

На E-шаге вычисляется значение скрытых переменных [math]g_{ij}[/math] по текущему приближению параметров [math]\Theta[/math].

[math]g_{ij} = \frac{w_jp_j(x_i)}{\sum_{s=1}^k w_sp_s(x_i)}[/math], что интерпретируется как вероятность принадлежности объекту [math]x_i[/math] к [math]j[/math]-ому кластеру.

M-шаг:

Будем максимизировать логарифм полного правдоподобия:

[math]Q(\Theta) = \ln\prod_{i=1}^mp(x_i) = \sum_{i=1}^m\ln\sum_{j=1}^kw_jp_j(x_i) \rightarrow \max_{\Theta}[/math], при условии [math]\sum_{j=1}^kw_j=1[/math]

Решением оптимизационной задачи являются формулы для пересчета параметров:

[math]w_j = \frac1m\sum_{i=1}^m g_{ij}[/math],

[math]\mu_j = \frac1{mw_j}\sum_{i=1}^m g_{ij}x_i[/math],

[math]\Sigma_j = \frac1{mw_j}\sum_{i=1}^m g_{ij}(x_i - \mu_j)(x_i - \mu_j)^T,\; j = 1, \dots, k[/math]

1.3 Вычислительное ядро алгоритма

Вычислительное ядро алгоритма представляет собой итерационное вычисление всех параметров модели, независимое по [math]m[/math] объектам выборки [math]X[/math]. На каждой итерации алгоритма на Е-шаге пересчитывается значение скрытых переменных, на M-шаге пересчет параметров модели с учетом скрытых переменных.

1.4 Макроструктура алгоритма

Как записано в описании ядра алгоритма, основную часть метода составляют вычисления элементов матрицы G на E шаге, и пересчет параметров [math]\Theta[/math] на M-шаге.

1.5 Схема реализации последовательного алгоритма

Инициализация параметров
for iter = 1 : max_iterations
[E-шаг]
1. вычисление [math]\Sigma_j^{-1}[/math] и [math]\frac1{(2\pi)^{d/2}\sqrt{|\Sigma_j|}}, j = 1 : k[/math]
2. вычисление [math]g_{ij},\;i = 1 : m, \; j = 1 : k[/math]
3. вычисление [math]LL_i[/math] (логарифм правдоподобия), [math]\;i = 1 : m[/math]
[M-шаг]
1. вычисление [math]\tilde w_j = \sum_{i=1}^m g_{ij}, \; j = 1 : m[/math]
2. вычисление [math]\tilde \mu_j = \sum_{i=1}^m g_{ij}x_i,\; j = 1 : k[/math]
3. вычисление [math]\tilde \Sigma_j = \sum_{i=1}^m g_{ij}(x_i - \mu_j)^T(x_i - \mu_j),\; j = 1 : k[/math]
4. нормировка [math]w_j = \frac{\tilde w_j}{m}[/math], [math]\mu_j = \frac{\tilde \mu_j}{w_j}, \tilde \Sigma_j = \frac{\tilde \Sigma_j}{w_j}, \;j = 1 : k[/math]
вычисление изменения логарифма правдоподобия[math]\Delta LL = fabs(\sum_{i=1}^m LL^{iter}_i - \sum_{i=1}^m LL^{iter - 1}_i)[/math]
if ([math]\Delta LL \lt \varepsilon[/math]) then break;
end for

1.6 Последовательная сложность алгоритма

E-шаг:

вычисление обратной матрицы [math]\Sigma_j^{-1}, j = 1 : k[/math] при фиксированном [math]j[/math] для двумерного случая по явным формулам имеет сложность [math]O(d^2)[/math], для всех кластеров — [math]O(d^2k)[/math]
вычисление [math]g_{ij}, i = 1 : m, j = 1 : k[/math] при фиксированных [math]i, j[/math] имеет сложность [math]O(d)[/math], сложность вычисления матрицы G — [math]O(dmk)[/math]
вычисление [math]LL_i, i = 1 : m[/math] при фиксированном [math]i[/math] имеет сложность [math]O(k)[/math], для всех объектов имеет сложность [math]O(mk)[/math],

M-шаг:

вычисление [math]w_j, j = 1 : k[/math] при фиксированном [math]j[/math] имеет сложность [math]O(m)[/math], для весов всех кластеров — [math]O(mk)[/math]
вычисление [math]\mu_j, j = 1 : k[/math] при фиксированном [math]j[/math] имеет сложность [math]O(dm)[/math], для всех кластеров — [math]O(dmk)[/math]
вычисление [math]\Sigma_j, j = 1 : k[/math] при фиксированном [math]j[/math] имеет сложность [math]O(d^2m)[/math], для всех кластеров — [math]O(d^2mk)[/math]
нормировка [math]w[/math], [math]\mu_j = \frac{\mu_j}{w_j}, \Sigma_j = \frac{\Sigma_j}{w_j}, j = 1 : k[/math] имеет сложность [math]O(k)[/math], [math]O(dk)[/math], [math]O(d^2k)[/math]
вычисление изменения логарифма правдоподобия[math]\Delta LL[/math] имеет сложность [math]O(1)[/math]

Сложность алгоритма на одной итерации:

[math]O(k(d^2+dm+m+m+dm+d^2m+1+d+d^2)) = O(d^2mk)[/math], так как мы рассматриваем задачу для двумерного случая, то есть [math]d=2[/math], множитель [math]d^2[/math] можно отнести в константу, итоговая сложность вычисления на одной итерации [math]O(mk)[/math].

Для [math]n[/math] итераций итоговая сложность алгоритма будет равна:

[math]O(mkn)[/math], где [math]m[/math] — число объектов, [math]k[/math] — число кластеров, [math]n[/math] — число итераций.

1.7 Информационный граф

Опишем граф алгоритма для следующих входных данных: [math]m = 3[/math], то есть 3 входных объекта.

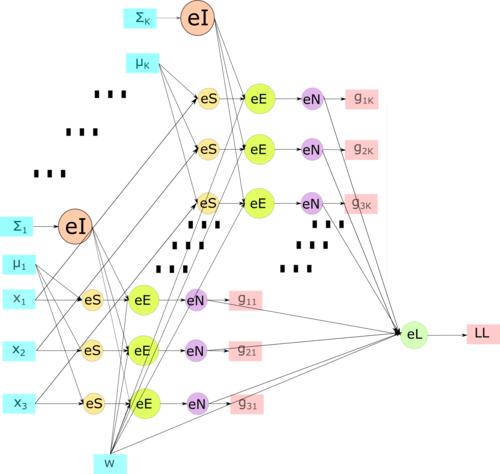
На рис.1 показана макроструктура EM-алгоритма. Входными данными в таком случае являются матрица [math]X \in \R^{3 \times 2}[/math], число кластеров [math]= K[/math]. На шаге [math]\mathbf{init}[/math] происходит инициализация начальных приближений параметров модели и затем итеративное повторение [math]\mathbf{E}[/math] и [math]\mathbf{M}[/math] шагов алгоритма.

Рис.1. Граф EM-алгоритма с отображением входных и выходных данных

E-шаг. На рис.2 детально изображена схема E-шага. Входные параметры [math]x_1,\; x_2,\; x_3 \in \R^{1 \times d}[/math] являются строчками входной матрицы [math]X[/math], также на вход подаются текущие приближения векторов средних значений ([math]\mu_1, \dots, \;\mu_K[/math]), матриц ковариаций ([math]\Sigma_1, \dots, \Sigma_K[/math]) и весов [math]w[/math].

Вершинами [math]\mathbf{eI}[/math] обозначена операция нахождения обратной матрицы [math]\Sigma_j^{-1},\; j = 1,\dots,K[/math]. Вершины группы [math]\mathbf{eS}[/math] обозначают вычитание векторов [math]x_i - \mu_j,\; i = 1,2,3; \; j = 1,\dots,K[/math]. Салатовые узлы графа [math]\mathbf{eE}[/math] обозначают вычисление ненормированного значения [math]g_{ij}, \;i = 1,2,3;\;j=1,\dots,K[/math] по формулам из раздела описания алгоритма. Далее выход вершин этой группы подаётся на вход вершинам [math]\mathbf{eN}[/math], которые обозначают нормировку, затем в [math]\mathbf{eL}[/math] происходит подсчет логарифма правдоподобия. На выходе этого графа получаются скрытые переменные [math]g_{ij}[/math] и логарифм правдоподобия LL.

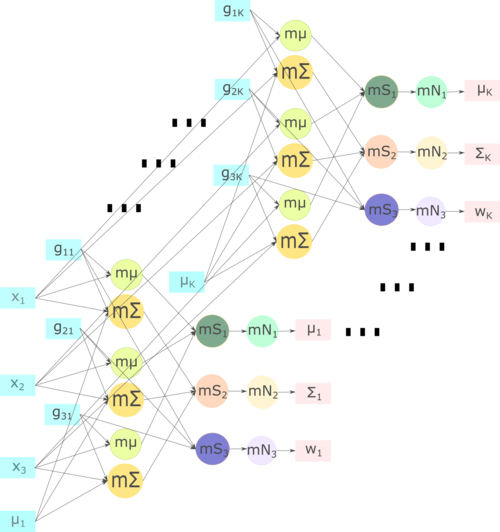
Рис.2. Граф E-шага с отображением входных и выходных данных

M-шаг. На рисунке 3 изображена схема M-шага. Входными параметрами являются: исходные объекты [math]x_1,\; x_2,\; x_3 \in \R^{1 \times 2}[/math], скрытые переменные [math]g_{11},\;g_{21},\;g_{31},\;\mu_1[/math] для пересчета параметров первого кластера и [math]g_{1K},\;g_{2K},\;g_{3K},\;\mu_K[/math] — для K-ого кластера.

Вершина [math]\mathbf{m}\boldsymbol{\mu}[/math] обозначает подсчет слагаемого математического ожидания для одного объекта, затем на шаге [math]\mathbf{mS_1}[/math] происходит суммирование слагаемых, и, наконец, на шаге [math]\mathbf{mN_1}[/math] нормировка математического ожидания, выходом являются [math]\mu_1,\dots,\;\mu_K[/math]. Вершина [math]\mathbf{m}\boldsymbol{\Sigma}[/math] обозначает подсчет слагаемого матрицы ковариации для одного объекта, затем на шаге [math]\mathbf{mS_2}[/math] происходит суммирование слагаемых, и, наконец, на шаге [math]\mathbf{mN_2}[/math] нормировка матрицы ковариации, выходом являются [math]\Sigma_1,\;\dots,\;\Sigma_K[/math]. Операция [math]\mathbf{mS_3}[/math] обозначает вычисление ненормированного веса для одного шага, затем при выполнении [math]\mathbf{mN_3}[/math] происходит нормировка весов, выходом являются [math]w_1,\dots,\;w_K[/math].

Рис.3. Граф M-шага с отображением входных и выходных данных

На рис.1 показана структура ЕM-алгоритма для кластеризации, на рис.2 — структура E-шага и на рис.3 — структура M-шага.

1.8 Ресурс параллелизма алгоритма

Как видно из информационного графа, возможно распараллеливание как по кластерам, так и по объектам. Однако, в реальных задачах число кластеров много меньше числа объектов, поэтому распараллеливание по кластерам нецелесообразно.

В данной статье рассматривается вариант распараллеливания по объектам. Стоит отметить, что важно корректно организовать работу с параметрами модели (матрицами ковариаций, средними значениями и весами), чтобы не произошло ситуации гонки за ресурсами ^[2].

1.9 Входные и выходные данные алгоритма

Входные данные: плотная вещественная матрица объектов-признаков [math]X \in \R^{m \times d}[/math] и количество кластеров [math]k[/math], где [math]m[/math] — количество объектов, [math]d[/math] — количество кластеров.

Объём входных данных: [math]m \times d + 1[/math].

Выходные данные: вектор весов [math]w \in \R^{k \times 1}[/math], [math]\;\;k[/math] векторов математических ожиданий [math]\mu_j \in \R^{d \times 1}[/math], [math]\;\;k[/math] матриц ковариации [math]\Sigma \in \R^{d \times d}[/math]

Объём выходных данных: [math]k \times (d \times d + d + 1)[/math]

1.10 Свойства алгоритма

EM-алгоритм не является устойчивым, результат его работы сильно зависит от начальных приближений параметров. При неудачном выборе начальных приближений алгоритм может не сойтись или сойтись в локальный экстремум.

Также, алгоритм не является детерминированным. Так как в начале работы алгоритма происходит инициализация начальных параметров случайным образом (с учетом положительной определенности и симметричности матрицы ковариации), он не может быть детерминирован.

Алгоритм сбалансирован по E и M шагам, затраты на выполнение этих этапов примерно одинаковы.

2 ЧАСТЬ. Программная реализация алгоритма

2.1 Особенности реализации последовательного алгоритма

В данном разделе приведем код реализации последовательного алгоритма.

double_vector em_algo::expectation_step(double_matrix& features)
{
    long n_objects = features.size1();
    int n_clusters = parameters.sigmas.size();
    double pi = boost::math::constants::pi<double>();

    // precalculate inverse matrices and dets
    std::vector<double_matrix> sigmas_inverted(n_clusters);
    std::vector<double> norm_distribution_denominator(n_clusters);
    for (int i = 0; i < n_clusters; ++i)
    {        
        double_matrix sigma_inverted(parameters.sigmas[i].size1(), parameters.sigmas[i].size2());
        double det = InvertMatrix(parameters.sigmas[i], sigma_inverted);
        if (det == 0)
        {
            std::cerr << "Matrix can not be inverted\n";
            exit(1);
        }
        norm_distribution_denominator[i] = sqrt(pow(2 * pi, parameters.n_features) * det);
        sigmas_inverted[i] = sigma_inverted;
    }

    hidden_vars = double_matrix(n_objects, n_clusters);
    double_vector log_likelihood(n_objects, 0);

    for (auto i = 0; i < n_objects; ++i)
    {
        double_matrix_row x(features, i);
        double norm_value = 0;
        for (auto j = 0; j < n_clusters; ++j)
        {
            double_matrix_column current_means(parameters.means, j);
            double_vector x_centered = x - current_means;

            double exp_power = -0.5 * inner_prod(prod(x_centered, sigmas_inverted[j]), x_centered);
            hidden_vars(i, j) = parameters.weights(j) * exp(exp_power) / norm_distribution_denominator[j];

            norm_value += hidden_vars(i, j);
        }
        double_matrix_row hidden_vars_row(hidden_vars, i);
        if (norm_value != 0)
        {
            hidden_vars_row = hidden_vars_row / norm_value;
            log_likelihood(i) = log(inner_prod(hidden_vars_row, parameters.weights));
        }

    }
    return log_likelihood;
}

void em_algo::maximization_step(double_matrix& features)
{
    int n_objects = features.size1();

    double_vector w = double_vector(n_clusters, 0.0);
    double_matrix means = double_matrix(parameters.n_features, n_clusters, 0.0);
    std::vector<double_matrix> sigmas;
    for (int j = 0; j < n_clusters; ++j)
        sigmas.push_back(double_matrix(parameters.n_features, parameters.n_features, 0.0));

    for (int i = 0; i < n_objects; ++i)
    {
        double_matrix_row x_i = row(features, i);

        for (int j = 0; j < n_clusters; ++j)
        {
            double g = hidden_vars(i, j);
            w(j) += g;

            double_matrix_column single_mean = column(means, j);

            single_mean += g * x_i;

            double_vector x_centered = x_i - column(parameters.means, j);
            for (int k = 0; k < parameters.n_features; ++k)
                for (int l = 0; l < parameters.n_features; ++l)
                    sigmas[j](k, l) = sigmas[j](k, l) + g * x_centered(k) * x_centered(l);
        }
    }
    // update weights
    parameters.weights = w / n_objects;

    for (int j = 0; j < n_clusters; ++j) {
        double weight = w(j);
        // update means
        double_matrix_column means_old = column(parameters.means, j);
        double_matrix_column means_new = column(means, j);
        means_old = means_new / weight;

        // update sigmas
        parameters.sigmas[j] = sigmas[j] / weight;
        for (int k = 0; k < parameters.n_features; ++k)
            parameters.sigmas[j](k, k) = parameters.sigmas[j](k, k) + tol;
    }
}

bool em_algo::is_likelihood_stabilized(double_vector likelihood, double_vector previous_likelihood)
{
    double likelihood_diff = sum(likelihood) - sum(previous_likelihood);
    return fabs(likelihood_diff) < tol;
}

model em_algo::process(double_matrix& features, int max_iterations)
{
    int iteration = 0;
    double_vector likelihood, previous_likelihood;
    while (iteration++ < max_iterations && (iteration <= 2 || !is_likelihood_stabilized(likelihood, previous_likelihood)))
    {
        previous_likelihood = likelihood;
        likelihood = expectation_step(features);
        maximization_step(features);
    }
    return parameters;
}

Возможной реализацией является перестановка местами циклов по объектам и по кластерам на E и М шаге. В данном случае внешний цикл проходит по объектам, так как подразумевается дальнейшая реализации распараллеливания по объектам. При реализации только последовательного алгоритма более понятной версией будет реализация внешнего цикла по кластерам, и внутреннего по объектам, но такая реализация увеличит число обращений в память и общее время работы алгоритма.

2.2 Локальность данных и вычислений

2.3 Возможные способы и особенности параллельной реализации алгоритма

2.4 Масштабируемость алгоритма и его реализации

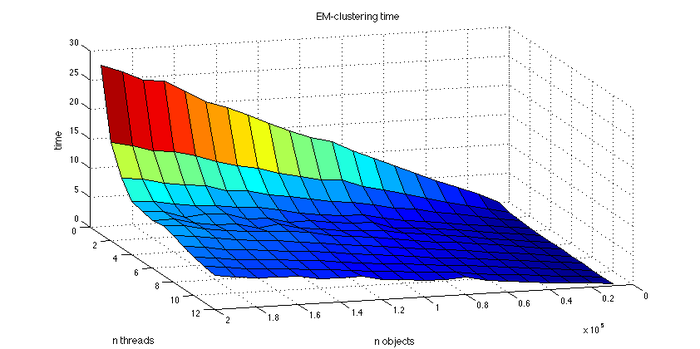
Для проведения экспериментов по масштабируемости были выбраны следующие параметры алгоритма: были зафиксированы число кластеров [math]k = 4 [/math], и, также, было зафиксировано ядро рандомизации, чтобы избавиться от случайности различного выбора начального приближения параметров. Для показательности результатов условие досрочного завершения работы алгоритма в случае стабилизации логарифма правдоподобия игнорировалось, и для каждого запуска проводилось 50 итераций EM-алгоритма.

Для экспериментов было сгенерировано 20 выборок разного размера: от 40000 объектов до 200000 с шагом в 10000. Для каждой выборки время работы алгоритма усреднялось по нескольким запускам, чтобы избежать выбросов.

Для работы с многопоточностью использовалась библиотека OpenMP. С помощью нее были распараллелены основные циклы по объектам на E и M шаге.

Эксперименты проводились на компьютере с процессором Intel(R) Core(TM) i7-5820K @ 3.30GHz, который поддерживает до 12ти потоков.

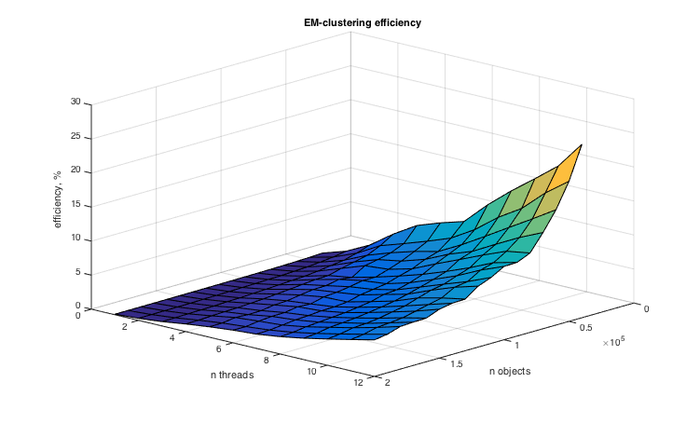
При увеличении числа процессоров производительность растёт. Заметим также, что с увеличением числа точек, скорость работы программы линейно увеличивается.

Рис. 4 Время работы EM алгоритма в зависимости от числа процессов и размера задачи

В результате проведённых экспериментов был получен следующий диапазон эффективности реализации алгоритма:

минимальная эффективность реализации 0,00072%;
максимальная эффективность реализации 25.5037%.

Рис. 5 Эффективность EM алгоритма в зависимости от числа процессов и размера задачи

2.5 Динамические характеристики и эффективность реализации алгоритма

2.6 Выводы для классов архитектур

2.7 Существующие реализации алгоритма

Существуют следующие последовательные реализации EM-алгоритма для кластеризации: opencv, scikit-learn.

Также существует несколько параллельных реализаций, описанных в следующих статьях:

В статье ^[3] авторы предлагают распределить вычисление скрытых переменных для каждого объекта между процессорами и на каждой итерации производить нормализацию. M-шаг предлагается параллелить по компонентам, что требует реализации корректного взаимодействия между процессорами. Предложенный вариант распараллеливания был реализован и протестирован авторами статьи с помощью MPI библиотеки MPICH.

Авторы статьи ^[4] используют MapReduce для распараллеливания EM-алгоритма для PLSI моделей.

3 Литература

↑ Воронцов К.В.; Математические методы обучения по прецедентам (теория обучения машин)
↑ Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. - СПб.: БХВ-Петербург, 2002. - 608 с.
↑ López-de-Teruel P. E., García J. M., Acacio; The Parallel EM Algorithm and its Applications in Computer Vision
↑ Abhinandan Das, Mayur Datar, Ashutosh Garg; Google News Personalization: Scalable Online Collaborative Filtering

[1] Воронцов К.В.; Математические методы обучения по прецедентам (теория обучения машин)

[2] Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. - СПб.: БХВ-Петербург, 2002. - 608 с.

[3] López-de-Teruel P. E., García J. M., Acacio; The Parallel EM Algorithm and its Applications in Computer Vision

[4] Abhinandan Das, Mayur Datar, Ashutosh Garg; Google News Personalization: Scalable Online Collaborative Filtering

[1]

[2]

[3]

[4]

Участник:Мария Готман/Алгоритм кластеризации, основанный на максимизации ожидания