Участник:Andrclive/Уравнения мелкой воды

Основные авторы описания: А.В.Чаплыгин

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Уравнения мелкой воды (МВ) представляют собой упрощенную модель полных уравнений Навье-Стокса, описывающих пространственные нестационарные течения. При выводе системы уравнений МВ предполагается, что среда представляет собой достаточно тонкий слой, глубина которого много меньше его продольного размера, поэтому вертикальной составляющей скорости в слое можно пренебречь и полагать, что продольные скорости постоянны по толщине слоя.

Ситуации, когда глубина акватории много меньше горизонтальных размеров, достаточно обычна, поэтому уравнения мелкой воды находят широкое применение. Они используются с учётом кориолисовых сил при моделировании атмосферы и океана. Именно этот случай будет рассматриваться.

Уравнения мелкой воды в криволинейной системе координат при предположении [math] \zeta \lt \lt H [/math], где [math]\zeta[/math] - это отклонение уровня, а [math]H[/math] - глубина, имеют вид:

[math] \left\{ \begin{array}{ccc} \frac{\partial u}{\partial t} - lv = -\frac{1}{r_x}( \frac{1}{\rho_0}\frac{\partial p_a}{\partial x} - g\frac{\partial \zeta}{\partial x} ) \\ \\ \frac{\partial v}{\partial t} + lu = -\frac{1}{r_y}( \frac{1}{\rho_0}\frac{\partial p_a}{\partial y} - g\frac{\partial \zeta}{\partial y} ) \\ \\ \frac{\partial \zeta}{\partial t} = \frac{1}{r_x r_y} ( \frac{\partial r_y u H}{\partial x} + \frac{\partial r_x v H}{\partial y} ) \\ \end{array} \right. [/math]

[math] u, v [/math] - зональная и меридиональная компоненты скорости, [math] l [/math] - параметр Кориолиса, [math] r_x, r_y [/math] - метрические коэффициенты, [math] p_a [/math] - атмосферное давление на поверхности, [math] g [/math] - ускорение свободного падения, [math] \rho_0 [/math] - средняя плотность жидкости.

1.2 Математическое описание алгоритма

Для решения уравнений применяется техника построения разностных аппроксимаций по пространству второго порядка точности (в случае равномерной сетки) на разнесенной "C" - сетке классификации Аракавы. Уравнения требуют совместного решения сразу трех уравнений, записанных с использованием неявной схемы по времени:

[math] \left\{ \begin{array}{ccc} \frac{u^{j+1} - u^j}{\delta t} - lv^{j+1} + ru^{j+1} = -\frac{1}{r_x}( \frac{1}{\rho_0}\frac{\partial p_a}{\partial x} - g\frac{\partial \zeta}{\partial x} ) \\ \\ \frac{v^{j+1} - v^j}{\delta t} + lu^{j+1} + rv^{j+1} = -\frac{1}{r_y}( \frac{1}{\rho_0}\frac{\partial p_a}{\partial y} - g\frac{\partial \zeta}{\partial y} ) \\ \\ \frac{\zeta^{j+1} - \zeta^j}{\delta t} = \frac{1}{r_x r_y} ( \frac{\partial r_y u H}{\partial x} + \frac{\partial r_x v H}{\partial y} ) \\ \end{array} \right. [/math]

Здесь в первые два уравнения дополнительно введены слагаемые, которые можно рассматривать как рэлеевское трение с коэффициентом [math] r [/math] для дополнительного стока импульса. Они необходимы для регуляризации задачи, поскольку система может быть вырожденной.

После дискретизации получаем линейную систему [math] Ax = b [/math], которую решаем итерационным методом GMRES.

1.3 Вычислительное ядро алгоритма

Формирование матрицы [math] A [/math] занимает довольно много времени и ресурсов при больших размерностях задачи, но матрица генерируется всего один раз в программе, в начале, затем на каждом шаге по времени генерируется правая часть [math] b [/math] и решается система [math] Ax = b [/math]. В процессе решения системы [math] Ax = b [/math] получается 7-диагональная плохо обусловленная матрица. Решать такую систему на каждом шаге по времени довольно затруднительно, особенно если шагов по времени довольно много, и поэтому основное время алгоритма приходится именно на этот этап.

1.5 Схема реализации последовательного алгоритма

1.6 Информационный граф

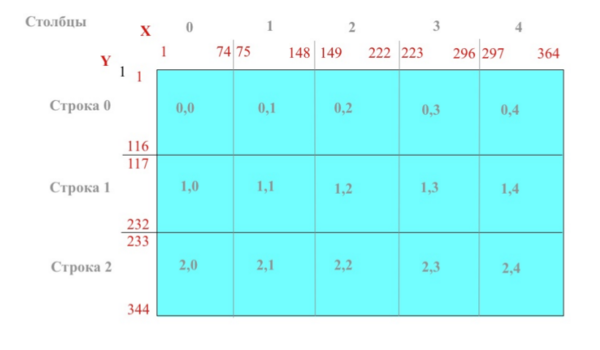
Параллельная реализация алгоритма использует метод двумерной декомпозиции области. При запуске программы из полученного числа процессоров формируется двумерная сетка, которая накладывается на рабочие массивы ([math] u, v, \zeta [/math]) во вертикале и горизонтали, в итоге каждый процессор получает свой блок из общего массива над которым он будет выполнять работу. На рисунке изображен пример разбиения массива по процессорной сетке:

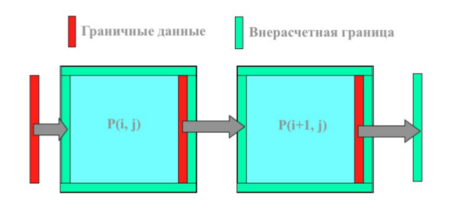
Дополнительные внерасчетные границы добавляются, чтобы производить обмен зависимыми данными между процессорами.

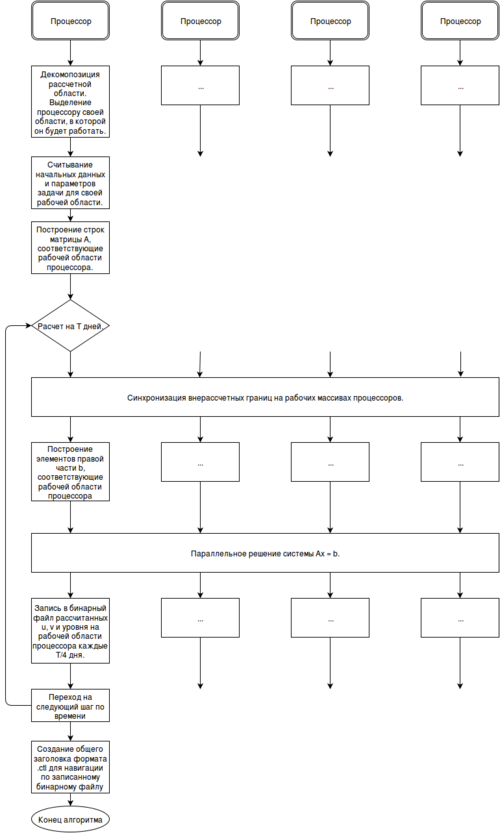
Приведем схему, показывающая структуру работы параллельной версии:

1.7 Входные и выходные данные алгоритма

В данном разделе необходимо описать объем, структуру, особенности и свойства входных и выходных данных алгоритма: векторы, матрицы, скаляры, множества, плотные или разреженные структуры данных, их объем. Полезны предположения относительно диапазона значений или структуры, например, диагональное преобладание в структуре входных матриц, соотношение между размером матриц по отдельным размерностям, большое число матриц очень малой размерности, близость каких-то значений к машинному нулю, характер разреженности матриц и другие.

2 Программная реализация алгоритма

2.1 Масштабируемость алгоритма и его реализации

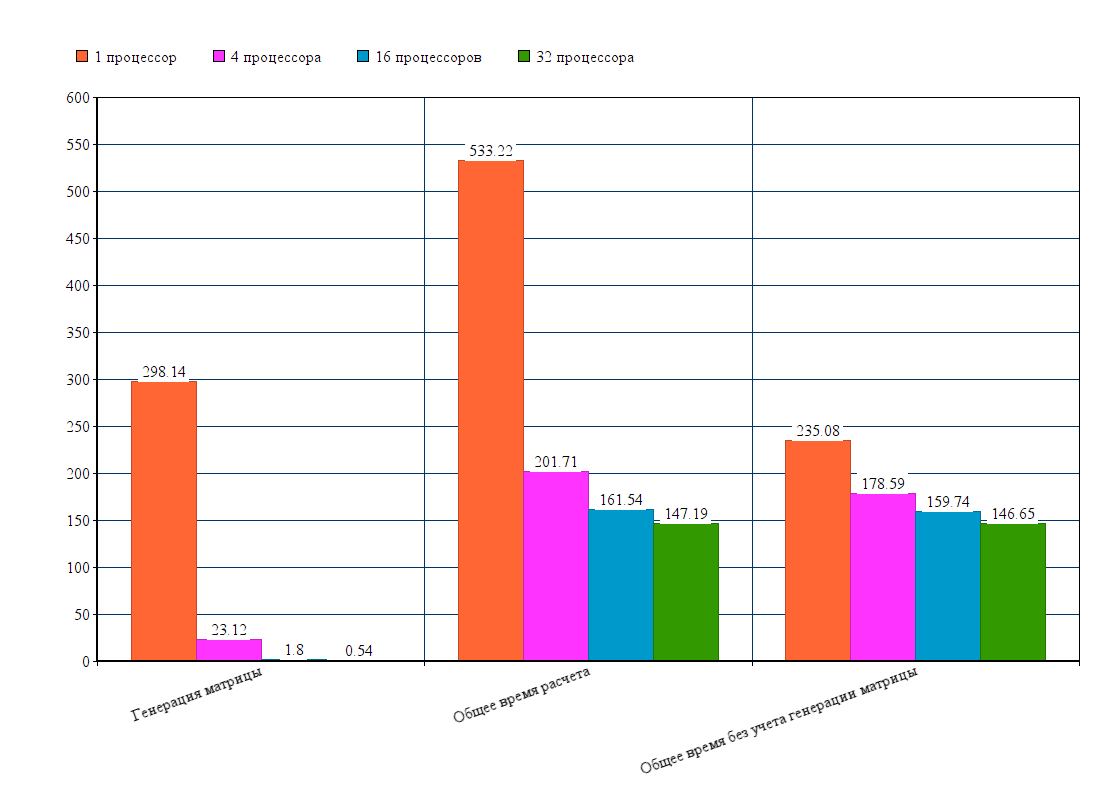
Задача рассчитывалась на сетке (1, 254)X(1, 128), на 5 дней с шагом по времени 1800 секунд (пол часа). Матрица [math] A [/math] на такой сетке имеет размеры 97920 на 97920. Все тесты проводились на суперкомпьютере Ломоносов.

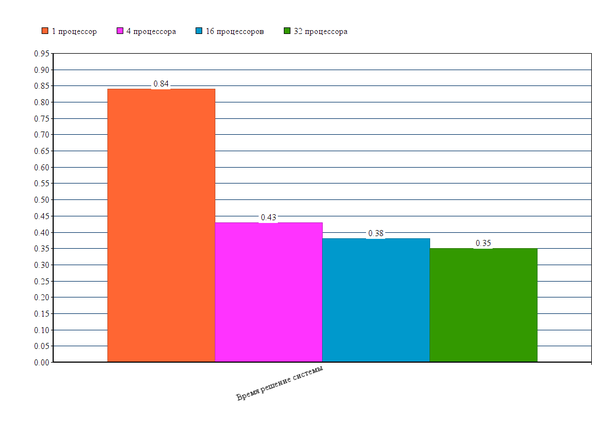
Общее время расчета алгоритма:

Время решения системы [math] Ax = b [/math] методом GMRES с помощью пакета PETSc для 50 итераций:

2.2 Существующие реализации алгоритма

Для многих пар алгоритм+компьютер уже созданы хорошие реализации, которыми можно и нужно пользоваться на практике. Данный раздел предназначен для того, чтобы дать ссылки на основные существующие последовательные и параллельные реализации алгоритма, доступные для использования уже сейчас. Указывается, является ли реализация коммерческой или свободной, под какой лицензией распространяется, приводится местоположение дистрибутива и имеющихся описаний. Если есть информация об особенностях, достоинствах и/или недостатках различных реализаций, то это также нужно здесь указать. Хорошими примерами реализации многих алгоритмов являются MKL, ScaLAPACK, PETSc, FFTW, ATLAS, Magma и другие подобные библиотеки.