Участник:Dmarkin/Алгоритм кластеризации, основанный на минимальном покрывающем дереве

Эта работа ждет рассмотрения преподавателем Дата последней правки страницы: 04.02.2017 Авторы этой статьи считают, что задание выполнено.

Автор описания: Маркин Дмитрий Валерьевич, группа 611

1 Свойства и структура алгоритмов

1.1 Общее описание алгоритма

Кластеризация (или кластерный анализ) — это задача разбиения множества объектов на группы, называемые кластерами. Внутри каждой группы должны оказаться «похожие» объекты, а объекты разных группы должны быть как можно более отличны.

Алгоритм кластеризации на [math]K[/math] кластеров, основанный на построении минимального остовного дерева ([math]MST[/math]):

1. По исходным данным строится граф. Каждый объект представляется в виде вершины графа, каждые две вершины соединяются ребром. Вычисляется вес ребра при помощи выбранной метрики (например, евклидовой);
2. Для полученного графа строится минимальное остовное дерево при помощи одного из алгоритмов (наиболее распространены: Алгоритм Крускала, Алгоритм Борувки, Алгоритм Прима)
3. Удаляется [math]K-1[/math] ребро минимального остовного дерева с максимальным весом и получаются k компонент связности.

1.2 Математическое описание алгоритма

Имеем [math]N[/math] объектов [math]x[/math], которые представляют собой элемент метрического пространства с метрикой [math]d(x_i,x_j)=\sqrt{\sum^{n}_{k=1} {(x_{ik}-x_{jk})^2}}[/math].

На первом шаге строим граф [math]G=(V,E)[/math] с множеством вершин [math]V[/math] ([math]|V|=N[/math]) и множеством ребер [math]E[/math] ([math]|E|=\frac{N*(N-1)} {2}[/math]).

На втором этапе строится минимальное покрывающее дерево [math]MST(G)[/math].

На третьем этапе удаляется [math]K-1[/math] ребро, и дерево распадается на поддеревья [math]MST_i[/math], вершины которых объявляются принадлежащими кластеру с номером [math]i[/math].

1.3 Вычислительное ядро алгоритма

Алгоритм состоит из трёх независимых шагов:

1. Построение графа и вычисление расстояний. Сложность [math]O(N^2)[/math];
2. Построение минимального покрывающего дерева при помощи одного из наиболее распространенных методов ( Алгоритм Крускала, Алгоритм Борувки, Алгоритм Прима). Сложность [math] O(N^2 \log N) [/math];
3. Разбиение на кластеры. Сложность в худшем случае [math]O(N)[/math].

Отсюда следует, что вычислительным ядром алгоритма является этап построения минимального покрывающего дерева, поскольку он имеет наибольшую сложность.

1.4 Макроструктура алгоритма

В состав алгоритма входят следующие макрооперации:

• Добавление ребра в граф;
• Вычисление расстояний между вершинами;
• Нахождение минимального покрывающего дерева, что является вычислительным ядром алогоритма;
• Удаление ребра из графа.

1.5 Схема реализации последовательного алгоритма

1.5.1 Обозначения

• [math]D(i) [/math] — расстояние от [math]i[/math]-й вершины до построенного дерева;
• [math]P(i) [/math] — предок [math]i[/math]-й вершины, то есть такая вершина [math]u[/math], что [math](u,i)[/math] легчайшее из всех рёбер, соединяющее [math]i[/math] с вершиной из построенного дерева;
• [math]W(i,j)[/math] — вес ребра [math](i,j)[/math];
• [math]Q[/math] — приоритетная очередь вершин графа, где ключ — [math]D(i)[/math];
• [math]T[/math] — множество ребер минимального остовного дерева.

1.5.2 Псевдокод

[math]T \gets  [/math] {} 
Для каждой вершины  [math] i \in V [/math] 
 [math]D(i) \gets \infty [/math]
 [math]P(i) \gets nil[/math]
 [math]D(1) \gets 0[/math]
 [math]Q \gets V[/math] 
Пока [math]Q [/math] не пуста
 [math]v \gets\ Extract.min(Q) [/math] 
 Для каждой вершины [math]u[/math] смежной с [math]v[/math]
  Если [math]u \in Q[/math] и [math]W(v,u) \lt  D(u)[/math]  
   [math]D(u) \gets W(v,u)[/math]
   [math]P(u) \gets v[/math]
 [math]v \gets Extract.Min(Q)[/math]
 [math]T \gets T+(P(v),v)[/math]

1.6 Последовательная сложность алгоритма

Последовательная сложность определяется суммой сложностей трёх основных этапов:

[math]T(N) = O(N^2) + O(N^2 \log N) + O(N) = O(N^2 \log N)[/math]

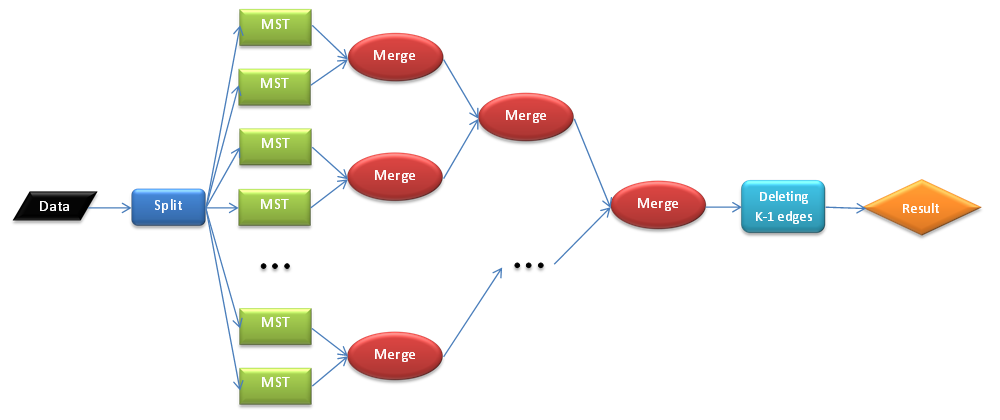
1.7 Информационный граф

Информационный граф параллельного алгоритма построения минимального покрывающего дерева

1.8 Ресурс параллелизма алгоритма

Рассмотрим основные свойства задачи:

• Схлопывание фрагментов. Пусть [math]F[/math] – фрагмент минимального остовного дерева графа [math]G[/math], а граф [math]G'[/math] получен из [math]G[/math] склеиванием вершин, принадлежащих [math]F[/math]. Тогда объединение [math]F[/math] и минимального остовного дерева графа [math]G'[/math] даёт минимальное остовное дерево исходного графа [math]G[/math].
• Ассоциативность по рёбрам. Пусть [math]MSF(E)[/math] – минимальный остовный лес графа с рёбрами [math]E[/math]. Тогда:[math] MSF(E_1 \cup E_2 \cup \dots \cup E_k) = MSF(MSF(E_1) \cup MSF(E_2) \cup \dots \cup MSF(E_k)). [/math]
• Минимальное ребро фрагмента. Пусть [math]F[/math] – фрагмент минимального остовного дерева и [math]e_F[/math] – ребро наименьшего веса, исходящее из [math]F[/math] (т.е. ровно один его конец является вершиной из [math]F[/math]). Если ребро [math]e_F[/math] единственно, то оно принадлежит минимальному остовному дереву. На этом свойстве основаны алгоритм Борувки и алгоритм Прима.

Ресурс параллелизма основан на следующих возможностях:

1. Свойства схлопывания фрагментов и минимального ребра фрагмента позволяют обрабатывать фрагменты независимо. Основанный на этих свойствах алгоритм Борувки обладает наибольшим ресурсом параллелизма среди трёх классических алгоритмов.
2. Ассоциативность по рёбрам может быть использована для параллелизации алгоритмов Крускала и Прима, которые изначально являются существенно последовательными.
3. Использование параллельных алгоритмов сортировки рёбер графа, либо параллельная сортировка рёбер у каждой вершины или у каждого фрагмента.

Существуют распределённые алгоритмы построения минимального покрывающего дерева, имеющие асимптотическую параллельную сложность [math]O(N \log N)[/math]. Например, Алгоритм GHS (Gallager, Humblet, Spira) является распределённым вариантом алгоритма Борувки. Последующие версии этого алгоритма имеют более низкую параллельную сложность.

1.9 Входные и выходные данные алгоритма

Входные данные: множество объектов [math]x = (x_1,...,x_N)[/math].

Выходные данные: множество кластеров [math]Clust = (Clust_1,...,Clust_K)[/math], где [math]Clust_i = (x_{i,1},..., x_{i, N_i}), x_{i, l} \ne x_{j, m}, i \ne j, \forall l[/math] и [math]m, \sum_{i=1}^K {N_i} = N [/math].

1.10 Свойства алгоритма

• Алгоритм останавливается за конечное число шагов, поскольку на каждом шаге становится по крайней мере на один фрагмент меньше.
• Число фрагментов на каждом шаге уменьшается как минимум вдвое, так что общее число шагов составляет не более [math]\log_2 N[/math].
• Соотношение последовательной и параллельной сложности: [math] \frac{N^2 \log N} {N \log N} = N [/math].
• Вычислительная мощность: [math] \frac {N^2 \log N} {N} = N \log N[/math].
• Алгоритм детерминирован. Если случается, что имеются два ребра [math](x_i,x_j)[/math] и [math](x_l,x_m)[/math], такие что [math]d(x_i,x_j) = d(x_l,x_m)[/math], то алгоритм должен выбрать ребро, одна из вершин которого имеет минимальный индекс [math]\min(i,j,l,m)[/math], если эти два ребра выходят из одной вершины, индекс которой является минимальным (например, [math]i=l[/math] ), то выбирается ребро, вершина которого имеет наименьший индекс из двух других вершин [math]\min(j,m)[/math].

2 Программная реализация алгоритма

2.7 Существующие реализации алгоритма

• Python: MST Clustering
• С++: Parallel boost graph library
• C++: Minimum Spanning Tree
• Java: JGraphT PrimMinimumSpanningTree
• Java: JGraphT KruskalMinimumSpanningTree
• Python: SciPy
• Python: NetworkX

3 Литература

1. Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. - СПб.: БХВ-Петербург, 2002. - 608 с.
2. Нейский И.М. Классификация и сравнение методов кластеризации
3. C. Kingsford. Minimum Spanning Trees & Clustering
4. Y. Zhou et al. Clustering with Minimum Spanning Trees
5. Gallager, Robert G, P A Humblet, and P M Spira. “A Distributed Algorithm for Minimum-Weight Spanning Trees.” ACM Transactions on Programming Languages and Systems 5, no. 1 (1983): 66–77. doi:10.1145/357195.357200.
6. Gafni, Eli. “Improvements in the Time Complexity of Two Message-Optimal Election Algorithms,” 175–85, New York, New York, USA: ACM Press, 1985. doi:10.1145/323596.323612.
7. Awerbuch, B. “Optimal Distributed Algorithms for Minimum Weight Spanning Tree, Counting, Leader Election, and Related Problems,” 230–40, New York, New York, USA: ACM Press, 1987. doi:10.1145/28395.28421.