Перемножение плотных неособенных матриц (последовательный вещественный вариант): различия между версиями
| [непроверенная версия] | [досмотренная версия] |
Frolov (обсуждение | вклад) (Новая страница: «== Описание свойств и структуры алгоритма == === Словесное описание алгоритма === '''Перемно…») |
ASA (обсуждение | вклад) |
||
| (не показано 39 промежуточных версий 10 участников) | |||
| Строка 1: | Строка 1: | ||
| − | + | {{level-a}} | |
| − | === | + | {{algorithm |
| + | | name = Перемножение плотных неособенных матриц | ||
| + | | serial_complexity = <math>2mnl</math> | ||
| + | | pf_height = <math>n</math> | ||
| + | | pf_width = <math>2ml</math> | ||
| + | | input_data = <math>mn+nl</math> | ||
| + | | output_data = <math>ml</math> | ||
| + | }} | ||
| + | |||
| + | Основные авторы описания: [[Участник:Frolov|А.В.Фролов]]. | ||
| + | |||
| + | == Свойства и структура алгоритма == | ||
| + | |||
| + | === Общее описание алгоритма === | ||
'''Перемножение матриц''' - одна из базовых задач в алгоритмах линейной алгебры, широко применяется в большом количестве разных методов. | '''Перемножение матриц''' - одна из базовых задач в алгоритмах линейной алгебры, широко применяется в большом количестве разных методов. | ||
| − | Здесь мы рассмотрим умножение <math> | + | Здесь мы рассмотрим умножение <math>C = AB</math> плотных неособенных матриц (последовательный вещественный вариант), то есть тот вариант, где никак не используются ни специальный вид матрицы, ни ассоциативные свойства операции сложения<ref>В.В.Воеводин, Ю.А.Кузнецов. Матрицы и вычисления. М.: Наука, 1984.</ref>. |
| − | === Математическое описание === | + | === Математическое описание алгоритма === |
Исходные данные: плотная матрица <math>A</math> (элементы <math>a_{ij}</math>), плотная матрица <math>B</math> (элементы <math>b_{ij}</math>). | Исходные данные: плотная матрица <math>A</math> (элементы <math>a_{ij}</math>), плотная матрица <math>B</math> (элементы <math>b_{ij}</math>). | ||
| Строка 15: | Строка 28: | ||
:<math> | :<math> | ||
\begin{align} | \begin{align} | ||
| − | c_{ij} = \sum_{k = 1}^{n} a_{ik} b_{kj}, \quad i \in [1, m], \quad | + | c_{ij} = \sum_{k = 1}^{n} a_{ik} b_{kj}, \quad i \in [1, m], \quad j \in [1, l]. |
\end{align} | \end{align} | ||
</math> | </math> | ||
| Строка 31: | Строка 44: | ||
=== Макроструктура алгоритма === | === Макроструктура алгоритма === | ||
| − | Как уже записано в [[#Вычислительное ядро алгоритма|описании ядра алгоритма]], основную часть умножения | + | Как уже записано в [[#Вычислительное ядро алгоритма|описании ядра алгоритма]], основную часть умножения матриц составляют множественные (всего <math>ml</math>) вычисления скалярных произведений строк матрицы <math>A</math> на столбцы матрицы <math>B</math> |
:<math>\sum_{k = 1}^{n} a_{ik} b_{kj}</math> | :<math>\sum_{k = 1}^{n} a_{ik} b_{kj}</math> | ||
| Строка 37: | Строка 50: | ||
в режиме накопления или без него. | в режиме накопления или без него. | ||
| − | === | + | === Схема реализации последовательного алгоритма === |
Для всех <math>i</math> от <math>1</math> до <math>m</math> и для всех <math>j</math> от <math>1</math> до <math>l</math> выполняются | Для всех <math>i</math> от <math>1</math> до <math>m</math> и для всех <math>j</math> от <math>1</math> до <math>l</math> выполняются | ||
| Строка 55: | Строка 68: | ||
* по <math>mnl</math> умножений и сложений. | * по <math>mnl</math> умножений и сложений. | ||
| − | При этом использование режима накопления требует совершения умножений и сложений в режиме двойной точности (или использования функции вроде DPROD в Фортране), что ещё больше увеличивает затраты во времени, требуемом для выполнения умножения | + | При этом использование режима накопления требует совершения умножений и сложений в режиме двойной точности (или использования функции вроде DPROD в Фортране), что ещё больше увеличивает затраты во времени, требуемом для выполнения умножения матриц. |
При классификации по последовательной сложности, таким образом, алгоритм умножения матриц относится к алгоритмам ''с кубической сложностью'' (в случае неквадратных матриц - с ''трилинейной''). | При классификации по последовательной сложности, таким образом, алгоритм умножения матриц относится к алгоритмам ''с кубической сложностью'' (в случае неквадратных матриц - с ''трилинейной''). | ||
| Строка 72: | Строка 85: | ||
Аргументы операции следующие: | Аргументы операции следующие: | ||
*<math>a</math>: | *<math>a</math>: | ||
| − | ** при <math>k = 1</math> константа <math>0 | + | ** при <math>k = 1</math> константа <math>0</math>; |
** при <math>k > 1</math> — результат срабатывания операции, соответствующей вершине с координатами <math>i, j, k-1</math>; | ** при <math>k > 1</math> — результат срабатывания операции, соответствующей вершине с координатами <math>i, j, k-1</math>; | ||
*<math>b</math> — элемент ''входных данных'', а именно <math>a_{ik}</math>; | *<math>b</math> — элемент ''входных данных'', а именно <math>a_{ik}</math>; | ||
| Строка 78: | Строка 91: | ||
Результат срабатывания операции является: | Результат срабатывания операции является: | ||
| − | + | * при <math>k < n</math> - ''промежуточным данным'' алгоритма; | |
| − | + | * при <math>k = n</math> - выходным данным <math>c_{ij}</math>. | |
| + | |||
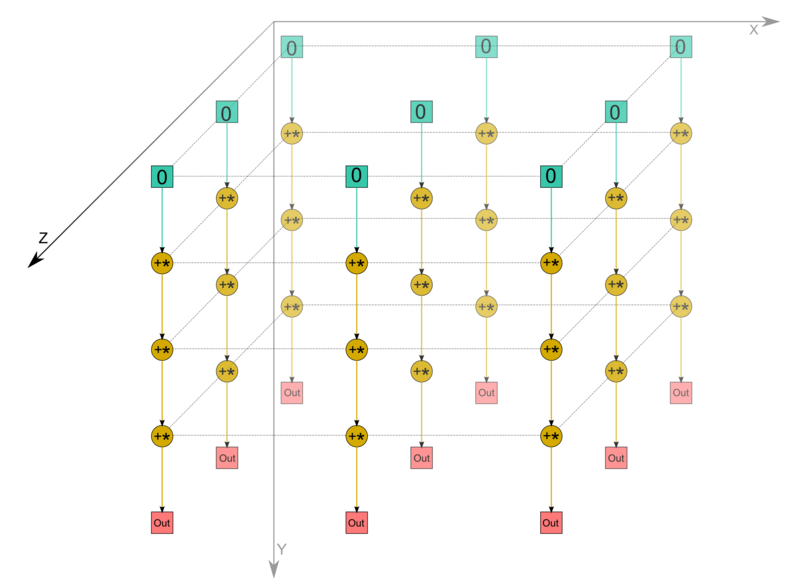
| + | [[file:Dense mtrx product.png|thumb|center|800px|Рисунок 1. Умножение плотных матриц с отображением выходных данных]] | ||
| + | <br/> | ||
| − | === | + | <center> |
| + | Интерактивное изображение графа алгоритма без входных и выходных данных для случая перемножения двух квадратных матриц порядка 3 и 4 | ||
| + | </center> | ||
| + | |||
| + | {{#widget:Algoviewer | ||
| + | |url=mat_mul/mat_mul_3/Algo_view_matrix3.html | ||
| + | |width=600 | ||
| + | |height=400 | ||
| + | |border=1 | ||
| + | }} | ||
| + | |||
| + | {{#widget:Algoviewer | ||
| + | |url=mat_mul/mat_mul_4/Algo_view_matrix4.html | ||
| + | |width=600 | ||
| + | |height=400 | ||
| + | |border=1 | ||
| + | }} | ||
| + | |||
| + | === Ресурс параллелизма алгоритма === | ||
Для алгоритма умножения квадратных матриц порядка n в параллельном варианте требуется последовательно выполнить следующие ярусы: | Для алгоритма умножения квадратных матриц порядка n в параллельном варианте требуется последовательно выполнить следующие ярусы: | ||
| Строка 93: | Строка 127: | ||
При этом использование режима накопления требует совершения умножений и вычитаний в режиме двойной точности, а в параллельном варианте это означает, что практически все промежуточные вычисления для выполнения алгоритма в режиме накопления должны быть двойной точности. В отличие от последовательного варианта это означает некоторое увеличение требуемой памяти. | При этом использование режима накопления требует совершения умножений и вычитаний в режиме двойной точности, а в параллельном варианте это означает, что практически все промежуточные вычисления для выполнения алгоритма в режиме накопления должны быть двойной точности. В отличие от последовательного варианта это означает некоторое увеличение требуемой памяти. | ||
| − | При классификации по высоте ЯПФ, таким образом, алгоритм умножения | + | При классификации по высоте ЯПФ, таким образом, алгоритм умножения матриц относится к алгоритмам ''с линейной сложностью''. При классификации по ширине ЯПФ его сложность также будет ''квадратичной'' (для квадратных матриц) или ''билинейной'' (для матриц общего вида). |
| − | === | + | === Входные и выходные данные алгоритма === |
| − | '''Входные данные''': матрица <math>A</math> (элементы <math>a_{ij}</math>), матрица <math>B</math> (элементы <math>b_{ij}</math>) | + | '''Входные данные''': матрица <math>A</math> (элементы <math>a_{ij}</math>), матрица <math>B</math> (элементы <math>b_{ij}</math>)). |
| − | '''Объём входных данных''': <math>mn+nl</math> | + | '''Объём входных данных''': <math>mn+nl</math> |
'''Выходные данные''': матрица <math>C</math> (элементы <math>c_{ij}</math>). | '''Выходные данные''': матрица <math>C</math> (элементы <math>c_{ij}</math>). | ||
| − | '''Объём выходных данных''': <math>ml</math> | + | '''Объём выходных данных''': <math>ml</math> |
=== Свойства алгоритма === | === Свойства алгоритма === | ||
| Строка 111: | Строка 145: | ||
При этом вычислительная мощность алгоритма умножения матриц, как отношение числа операций к суммарному объему входных и выходных данных – ''линейно''. | При этом вычислительная мощность алгоритма умножения матриц, как отношение числа операций к суммарному объему входных и выходных данных – ''линейно''. | ||
| − | При этом алгоритм умножения | + | При этом алгоритм умножения матриц полностью детерминирован. Использование другого порядка выполнения ассоциативных операций в данной версии нами не рассматривается. |
| − | == Программная реализация == | + | == Программная реализация алгоритма == |
=== Особенности реализации последовательного алгоритма === | === Особенности реализации последовательного алгоритма === | ||
| Строка 133: | Строка 167: | ||
При этом для реализации режима накопления переменная <math>S</math> должна быть двойной точности. | При этом для реализации режима накопления переменная <math>S</math> должна быть двойной точности. | ||
| − | + | === Возможные способы и особенности параллельной реализации алгоритма === | |
| − | + | === Результаты прогонов === | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === Возможные способы и особенности реализации | ||
| − | |||
| − | |||
| − | === | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
=== Выводы для классов архитектур === | === Выводы для классов архитектур === | ||
| + | == Литература == | ||
| + | <references /> | ||
| − | + | [[Категория:Законченные статьи]] | |
| − | + | [[Категория:Матричные операции]] | |
| − | |||
| − | + | [[En:Dense matrix multiplication (serial version for real matrices)]] | |
Текущая версия на 16:21, 19 февраля 2025
| Перемножение плотных неособенных матриц | |
| Последовательный алгоритм | |
| Последовательная сложность | 2mnl |
| Объём входных данных | mn+nl |
| Объём выходных данных | ml |
| Параллельный алгоритм | |
| Высота ярусно-параллельной формы | n |
| Ширина ярусно-параллельной формы | 2ml |
Основные авторы описания: А.В.Фролов.
Содержание
- 1 Свойства и структура алгоритма
- 1.1 Общее описание алгоритма
- 1.2 Математическое описание алгоритма
- 1.3 Вычислительное ядро алгоритма
- 1.4 Макроструктура алгоритма
- 1.5 Схема реализации последовательного алгоритма
- 1.6 Последовательная сложность алгоритма
- 1.7 Информационный граф
- 1.8 Ресурс параллелизма алгоритма
- 1.9 Входные и выходные данные алгоритма
- 1.10 Свойства алгоритма
- 2 Программная реализация алгоритма
- 3 Литература
1 Свойства и структура алгоритма
1.1 Общее описание алгоритма
Перемножение матриц - одна из базовых задач в алгоритмах линейной алгебры, широко применяется в большом количестве разных методов. Здесь мы рассмотрим умножение C = AB плотных неособенных матриц (последовательный вещественный вариант), то есть тот вариант, где никак не используются ни специальный вид матрицы, ни ассоциативные свойства операции сложения[1].
1.2 Математическое описание алгоритма
Исходные данные: плотная матрица A (элементы a_{ij}), плотная матрица B (элементы b_{ij}).
Вычисляемые данные: плотная матрица C (элементы c_{ij}).
Формулы метода:
- \begin{align} c_{ij} = \sum_{k = 1}^{n} a_{ik} b_{kj}, \quad i \in [1, m], \quad j \in [1, l]. \end{align}
Существует также блочная версия метода, однако в данном описании разобран только точечный метод.
1.3 Вычислительное ядро алгоритма
Вычислительное ядро перемножения плотных неособенных матриц можно составить из множественных (всего их l) вычислений умножения матрицы A на столбцы матрицы B, или (при более детальном рассмотрении), из множественных (всего их ml) скалярных произведений строк матрицы A на столбцы матрицы B:
- \sum_{k = 1}^{n} a_{ik} b_{kj}
в режиме накопления или без него, в зависимости от требований задачи.
1.4 Макроструктура алгоритма
Как уже записано в описании ядра алгоритма, основную часть умножения матриц составляют множественные (всего ml) вычисления скалярных произведений строк матрицы A на столбцы матрицы B
- \sum_{k = 1}^{n} a_{ik} b_{kj}
в режиме накопления или без него.
1.5 Схема реализации последовательного алгоритма
Для всех i от 1 до m и для всех j от 1 до l выполняются
- c_{ij} = \sum_{k = 1}^{n} a_{ik} b_{kj}
Особо отметим, что вычисления сумм вида \sum_{k = 1}^{n} a_{ik} b_{kj} производят в режиме накопления прибавлением к текущему (временному) значению вычисляемого элемента матрицы c_{ij} произведений a_{ik} b_{kj} для k от 1 до n, c возрастанием k, вначале все элементы инициализируются нулями. При суммировании "по убыванию" общая схема принципиально не отличается и потому нами не рассматривается. Другие порядки выполнения суммирования приводят к изменению параллельных свойств алгоритма и будут рассматриваться нами в отдельных описаниях.
1.6 Последовательная сложность алгоритма
Для умножения двух квадратных матриц порядка n (т.е. при m=n=l) в последовательном (наиболее быстром) варианте требуется:
- по n^3 умножений и сложений.
Для умножения матрицы размером m строк на n столбцов на матрицу размером m строк на n столбцов в последовательном (наиболее быстром) варианте требуется:
- по mnl умножений и сложений.
При этом использование режима накопления требует совершения умножений и сложений в режиме двойной точности (или использования функции вроде DPROD в Фортране), что ещё больше увеличивает затраты во времени, требуемом для выполнения умножения матриц.
При классификации по последовательной сложности, таким образом, алгоритм умножения матриц относится к алгоритмам с кубической сложностью (в случае неквадратных матриц - с трилинейной).
1.7 Информационный граф
Опишем граф алгоритма как аналитически, так и в виде рисунка.
Граф алгоритма умножения плотных матриц состоит из одной группы вершин, расположенной в целочисленных узлах трёхмерной области, соответствующая ей операция a+bc.
Естественно введённые координаты области таковы:
- i — меняется в диапазоне от 1 до m, принимая все целочисленные значения;
- j — меняется в диапазоне от 1 до l, принимая все целочисленные значения;
- k — меняется в диапазоне от 1 до n, принимая все целочисленные значения.
Аргументы операции следующие:
- a:
- при k = 1 константа 0;
- при k \gt 1 — результат срабатывания операции, соответствующей вершине с координатами i, j, k-1;
- b — элемент входных данных, а именно a_{ik};
- c - элемент входных данных b_{kj};
Результат срабатывания операции является:
- при k \lt n - промежуточным данным алгоритма;
- при k = n - выходным данным c_{ij}.
Интерактивное изображение графа алгоритма без входных и выходных данных для случая перемножения двух квадратных матриц порядка 3 и 4
1.8 Ресурс параллелизма алгоритма
Для алгоритма умножения квадратных матриц порядка n в параллельном варианте требуется последовательно выполнить следующие ярусы:
- по n ярусов умножений и сложений (в каждом из ярусов — n^2 операций).
Для умножения матрицы размером m строк на n столбцов на матрицу размером n строк на l столбцов в последовательном (наиболее быстром) варианте требуется:
- по n ярусов умножений и сложений (в каждом из ярусов — ml операций).
При этом использование режима накопления требует совершения умножений и вычитаний в режиме двойной точности, а в параллельном варианте это означает, что практически все промежуточные вычисления для выполнения алгоритма в режиме накопления должны быть двойной точности. В отличие от последовательного варианта это означает некоторое увеличение требуемой памяти.
При классификации по высоте ЯПФ, таким образом, алгоритм умножения матриц относится к алгоритмам с линейной сложностью. При классификации по ширине ЯПФ его сложность также будет квадратичной (для квадратных матриц) или билинейной (для матриц общего вида).
1.9 Входные и выходные данные алгоритма
Входные данные: матрица A (элементы a_{ij}), матрица B (элементы b_{ij})).
Объём входных данных: mn+nl
Выходные данные: матрица C (элементы c_{ij}).
Объём выходных данных: ml
1.10 Свойства алгоритма
Соотношение последовательной и параллельной сложности в случае неограниченных ресурсов, как хорошо видно, является квадратичным или билинейным (отношение кубической или трилинейной к линейной).
При этом вычислительная мощность алгоритма умножения матриц, как отношение числа операций к суммарному объему входных и выходных данных – линейно.
При этом алгоритм умножения матриц полностью детерминирован. Использование другого порядка выполнения ассоциативных операций в данной версии нами не рассматривается.
2 Программная реализация алгоритма
2.1 Особенности реализации последовательного алгоритма
В простейшем варианте алгоритм умножения матриц на Фортране можно записать так:
DO I = 1, M
DO J = 1, L
S = 0.
DO K = 1, N
S = S + DPROD(A(I,K), B(K,J))
END DO
C(I, J) = S
END DO
END DO
При этом для реализации режима накопления переменная S должна быть двойной точности.
2.2 Возможные способы и особенности параллельной реализации алгоритма
2.3 Результаты прогонов
2.4 Выводы для классов архитектур
3 Литература
- ↑ В.В.Воеводин, Ю.А.Кузнецов. Матрицы и вычисления. М.: Наука, 1984.