Стабилизированный метод бисопряженных градиентов (BiCGStab)

Авторы описания: А.Новиков (разделы 1.4, 1.6, 1.7, 2.4, 2.7, 3), А.Гаврилов (разделы 1.1-1.3, 1.5, 1.8, 1.9, 2.7, 3)

BiCGStab
Последовательный алгоритм
Последовательная сложность	[math] O(I \cdot N^2) [/math], где [math] N [/math] - размерность СЛАУ, [math]I[/math] - количество итераций
Объём входных данных	матрица [math]A \in R^{N \times N}[/math] ( [math]C^{N \times N}[/math] ) и вектор правой части [math]b \in R^N[/math] ( [math]C^N[/math] )
Объём выходных данных	вектор решения системы [math]x \in R^N[/math] ( [math]C^N[/math] )
Параллельный алгоритм
Высота ярусно-параллельной формы	[math] O(k\cdot(6 \sqrt N + 4N + 5 \lceil \frac{N}{p} \rceil)) [/math]
Ширина ярусно-параллельной формы	[math] 2 \sqrt N [/math]

1 Свойства и структура алгоритма

1.1 Общее описание алгоритма

Стабилизированный метод бисопряженных градиентов, так же известный как BiCGStab (BiConjugate Gradient Stabilized method), был предложен голландским математиком Хенком ван дер Ворстом в 1992 году. Статья, в которой описывался метод, стала самым цитируемым научным трудом в области математики в 1990х годах.

Метод появился, как ответ на задачу о построении способа решения систем линейных алгебраических уравнений произвольного вида. На момент появления BiCGStab уже существовали методы решения СЛАУ произвольного типа, в том числе и в комплексном пространстве, например метод бисопряженных градиентов. Однако существующие на тот момент методы либо обладали недостаточной скоростью сходимости, либо использовали в вычислениях тяжелые операции, такие как транспонирования матрицы, которые усложняли распараллеливание на многопроцессорных машинах.

BiCGStab является итерационным методом решения систем линейных алгебраических уравнений. Мощь метода заключается в том, что его можно применять к матрицам общего вида, в том числе с комплексными коэффициентами. В процессе выполнения BiCGStab не использует для вычисления плохо распараллеливаемых операций, не допускает накопления погрешностей округления и нестабильного поведения невязки. Эти факторы выгодно отличают его от предшественников: метода бисопряженных градиентов и квадратичного метода сопряженных градиентов, из которого BiCGStab фактически и вытекает. К преимуществам так же можно добавить более высокую в общем случае скорость сходимости относительно ближайших конкурентов. Тем не менее, для некоторых видов СЛАУ BiCGStab может уступать более простым методам.

Благодаря свойствам алгоритма область применения метода весьма широка. Фактически, он используется во всех задачах, где требуется решать СЛАУ, в том числе СЛАУ большой размерности, к которым сводится большое количество численных методов, применяемых при решении задач математического моделирования.

BiCGStab относится к классу так называемых проекционных методов. Основная идея методов данного класса: искать итерационным способом наилучшее приближение решения в некотором подпространстве пространства [math]R^n[/math], и чем шире подпространство, в котором ищется приближение решения, тем ближе будет приближенное решение к точному на каждой итерации. В качестве такого подпространства используются пространства Крылова, порожденные матрицей системы и невязкой первого приближения: [math]K^m (A, r^0) = \rm span(r^0, Ar^0, A^2r^0, ..., A^{m-1} r^0)[/math].

Изложим основную идею любого проекционного метода, заложенную в том числе и в BiCGStab. Для простоты выкладок и рассуждений здесь и далее будем считать, что матрица системы и ее правая часть вещественны. Без ограничения общности все дальнейшие рассуждения могут быть перенесены и на комплексный случай. Итак, пусть решается система [math]Ax=b[/math] с невырожденной матрицей [math]A \in R^{n \times n}[/math] и ненулевым вектором [math]b \in R^n[/math]. Имеются два подпространства [math]K_n[/math] и [math]L_n[/math]. Требуется найти вектор [math]x \in K_n[/math], который обеспечивает решение системы, оптимальное относительно подпространства [math]L[/math], то есть требуется выполнение условия Петрова-Галеркина: [math](Ax,z)=(b,z), \forall z \in L_n[/math]. В данном случае вектор x называется обобщенным решением системы.

Условие Петрова-Галеркина можно записать и через определение невязки. Пусть [math]r = b - Ax[/math] - невязка, тогда условие Петрова-Галеркина перепишется в виде: [math](b - Ax, z)=(r, z),\forall z \in L_n[/math]. Это равносильно тому, что вектор невязки ортогонален пространству [math]L_n[/math].

Пусть для СЛАУ известно некоторое приближение [math]x^0[/math] точного решения [math]x^*[/math]. Данное приближение требуется уточнить поправкой [math] \delta: b - Ax^0 + \delta \perp L[/math]. Невязка уточненного решения имеет вид: [math]r_{new} = b - Ax^0 + \delta = r^0- A\delta[/math]. Условие Петрова-Галеркина тогда можно переписать так: [math](r_{new}, z)= r^0 - (A\delta, z) = 0, \forall z \in L[/math]

Пусть [math]\rm dim K = dim L = m, V = (v_1, ..., v_n) \in R^{n \times m}, W = (w_1, ... w_n) \in R^{n \times m}[/math], где [math]V[/math] и [math]W[/math] – матрицы, столбцы которых образуют базисы пространств [math]K[/math] и [math]L[/math] соответственно. Пусть так же [math] \delta = Vy, z = Wq[/math], где [math]y[/math] – коэффициенты разложения вектора поправки по базису пространства [math]K[/math], а [math]q[/math] – коэффициенты разложения вектора [math]z[/math] в пространстве [math]L[/math]. Тогда новое приближение решения можно записать в виде: [math]x^1 = x^0 + \delta= x^0 + Vy[/math]. Из условия ортогональности Петрова-Галеркина получаем, что: [math](r - AVy, Wq) = (W^Tr^0 - AVy, q) = 0[/math]. Поскольку [math]q \neq 0[/math], то получаем СЛАУ для вектора [math]y[/math]: [math]W^TAVy = W^Tr^0[/math]. Если предположить, что матрица [math]W^TAVy[/math] невырождена, то вектор y однозначно определяется и равен: [math]y = W^TAV^{-1}W^Tr^0[/math]. Подставляя найденные коэффициенты разложения в выражение для первого приближения получаем: [math]x^1 = x^0 + \delta = x^0 + W^TAV^{-1}W^Tr^0y[/math]

Подведем итог. Общий порядок шагов любого проекционного метода следующий:

1. Выбрать пару подпространств [math]K[/math] и [math]L[/math]
2. Найти базис V пространства K и базис W пространства [math]L[/math];
3. Вычислить невязку
4. Найти [math]y = W^T AV^{-1} W^T r^0[/math]
5. Положить [math]x = x + Vy[/math]
6. Если не достигнут критерий остановки итерационного процесса, то повторить алгоритм, начиная с первого шага.

Как будет показано далее, в BiCGStab не требуется вычислять матрицу [math]W^T AV^{-1}[/math] в явном виде.

1.2 Математическое описание алгоритма

Рассмотрим СЛАУ с вещественными коэффициентами:

[math]Ax = b, \quad A \in R^{N \times N}, \quad b \in R^N.[/math]

В основу алгоритма ложиться идея проекционного метода и использование свойства A-бисопряженности системы векторов, а именно: векторы [math]p^1, p^2, ...[/math] и [math]\overline p^1, \overline p^2, ...[/math] бисопряжены, если [math](Ap^i,p^j ) = 0[/math], при [math]i \neq j[/math]. Фактически, данное условие эквивалентно биортогональности относительно энергетического скалярного произведения.

Общая концепция проекционных методов предписывает нам выбрать два подпространства. В нашем случае подпространства мы выберем два подпространства, задаваемые матрицей системы А, вектором невязки на нулевой итерации [math]r^0[/math] и вектором [math]\overline r^0[/math]. который выбирается из условия [math](r^0, \overline r^0) \neq 0[/math]:

[math]K = K^k(A, r^0),\quad L = K^k(A, \overline r^0).[/math]

Метод основан на построении биортогонального базиса [math]p^0, p^1, ..., p^k, ... [/math] пространства [math]K^k (A, r^0) [/math] и вычислении поправки такой, что новое приближение на очередной итерации было бы ортогонально второму подпространству Крылова. Базисные вектора строятся до тех пор, пока не будет достигнут критерий остановки итерационного процесса, а каждое последующее приближение формируется, как сумма приближения на предыдущей итерации и найденной поправки. Критерием останова итерационного процесса является достижение невязкой значения, которое меньше некоторого наперед заданного [math]\epsilon[/math].

Основной итерационный процесс задается формулами:

[math]x^{k + 1} = x^k + \alpha_k p_k + \omega_k s_k[/math] [math]p^{k + 1} = r^{k + 1} + \beta_k p_k - \omega_k Ap_k[/math]

где:

1. [math]x^{k + 1}[/math] - приближение на следующей итерации
2. [math]x^k[/math] - приближение на предыдущей итерации
3. [math]p_k[/math] - базисный вектор подпространства Крылова, порожденного матрице СЛАУ и невязкой
4. [math]\alpha_k, \omega_k[/math] - вспомогательные скаляры, определяемые для каждого шага итерации
5. [math]s_k[/math] - вспомогательный вектор
6. [math]p^{k + 1}[/math] - [math]k + 1[/math]-ый базисный вектор
7. [math]r^{k + 1}[/math] - невязка [math]k + 1[/math]-ой итерации
8. [math]\beta_k[/math] - вспомогательный коэффициент

Вспомогательный вектор выражается следующим образом:

• [math]s_k = r^k - \alpha_k Ap_k[/math]

Вспомогательные коэффициенты вычисляются по формулам:

• [math]\alpha_k = \frac{(r^k, \overline r^0)}{(Ap_k, \overline r^0)}[/math]
• [math]\omega_k = \frac{(As_k, s_k)}{(As_k, As_k)}[/math]
• [math]\beta_k = \frac{(r^{k + 1}, \overline r^0)}{(r^k, \overline r^0)}[/math]

Подведем итог и запишем итерационный процесс

Подготовительный этап:

1. Выбирается некоторое начальное приближение [math]x^0[/math]
2. По выбранному приближению находится невязка [math]r^0 = b - Ax^0[/math]
3. Из условия [math](r^0, \overline r^0) \neq 0[/math] выбирается вектор [math]\overline r^0[/math]
4. Положим [math]p^0 = r^0[/math]
5. Устанавливаем счетчик итераций: [math]n = 0[/math]

Итерационный процесс:

1. Находим [math]\alpha_k[/math]
2. По найденному [math]\alpha_k[/math] вычисляем [math]s_k[/math]
3. По найденному [math]s_k[/math] вычисляется вспомогательный коэффициент [math]\omega_k[/math]
4. Находится новое приближение [math]x^{k + 1}[/math]
5. Вычисляется невязка [math]r^{k + 1}[/math]. Если выполнено условие [math]\parallel r^{k + 1} \parallel \lt \epsilon[/math], то алгоритм завершается.
6. Вычисляется вспомогательный коэффициент [math]\beta_k[/math]
7. Вычисляется новый базисный вектор: [math]p^{k + 1}[/math]
8. Увеличивается номер итерации: [math]n = n + 1[/math]
9. Переход к первому шагу итерационного процесса.

1.3 Вычислительное ядро алгоритма

Вычислительное ядро полностью совпадает с итерационным процессом. Подготовка к итерационному процессу в ядро не включается.

1.4 Макроструктура алгоритма

На каждой итерации алгоритма используются:

1. Скалярное произведение векторов, вещественная версия, последовательно-параллельный вариант x 4 раза
2. Умножение плотной матрицы на вектор х 2 раза

1.6 Последовательная сложность алгоритма

Всего в вычислительном блоке алгоритма присутствует 20 трудоемких операций: 2 операции умножения матрицы на вектор, 6 скалярных произведений и 6 сложений/вычитаний векторов и 6 умножений вектора на число.

Каждое скалярное произведение требует [math]N[/math] произведений и [math]N - 1[/math] сложение, то есть [math]2N - 1[/math] операции. Скалярных произведений всего 6 штук (включая поиск нормы), что дает нам [math]12N - 6[/math] операций.

Умножение матрицы размерности [math]N \times N[/math] на вектор эквивалентно взятию еще [math]N[/math] скаляров, и так как таких операций в вычислительном ядре 2, то дополнительно имеется еще [math]2N(2N - 1)[/math] операций.

Наконец, сложение или вычитание векторов требует [math]6N[/math] соотвествующих операций. Столько же требует 6 произведений вектора на число.

Итого: [math]2N(2N - 1) + 12N - 6 + 6N + 6N = 4N^2 + 22N - 6[/math] операций за одну итерацию. Домножая это на количество итераций [math]I[/math], получаем итоговую сложность алгоритма: [math]I \cdot (4N^2 + 22N - 6)[/math]

Имеются так же операции как, извлечение квадратного корня и деление вещественных чисел друг на друга, но они не принимаются в расчет, так как они не влияют на итоговый результат. Окончательно можно заключить, что последовательная сложность алгоритма эквивалента [math]O(I \cdot N^2)[/math]

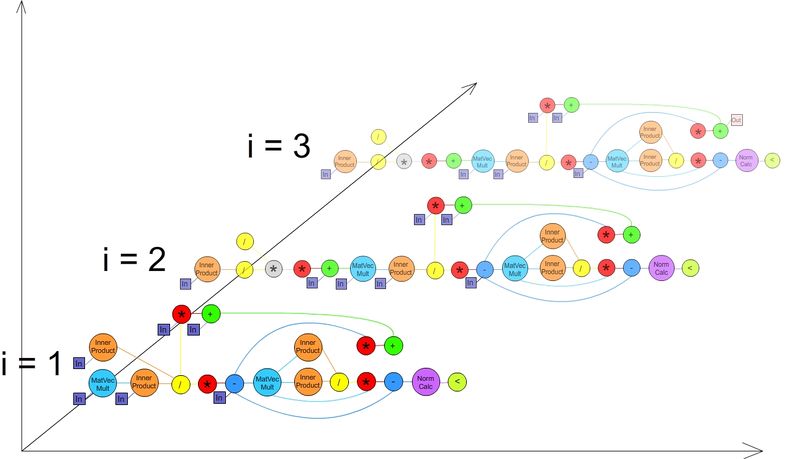
1.7 Информационный граф

Информационный граф.

На графе представлены связи между операциями, выполняющимися в первых трех итерациях метода. При выполнении большего, чем 3, количества итераций, структура каждой новой будет повторять структуру третьей. Связи между итерациями не представлены, т.к. они не важны для понимания параллельной структуры алгоритма. Серым обозначено перемножение чисел, красным - умножение числа на вектор

1.8 Ресурс параллелизма алгоритма

Основной прирост производительности параллельной версии алгоритма дает использование параллельных операций вычисления скалярного произведения, суммы векторов, а так же произведения матрицы на вектор. Каждая из операций вычисления скалярного произведения и суммы векторов, выполняемая на [math]p[/math] процессорах, за счет метода сдваивания может ускориться до [math] \frac{p}{\log_2 p} [/math] раз. Ускорение же умножения матрицы на вектор может достигать [math]p[/math] раз.

Ширина и высота ЯПФ графа данного алгоритма напрямую зависит от конкретных реализаций макроопераций и входных данных.

Для последовательно-параллельной реализации операции взятия скалярного произведения в наиболее оптимальном случае ([math]p= \sqrt N[/math]) высота будет равна [math]2 \sqrt N - 1[/math], а ширина [math]\sqrt N[/math], где [math]N[/math] - это длина вектора решения.

Высота ЯПФ простейшего алгоритма умножения матрицы на вектор равна [math]2N[/math], а ширина [math]m[/math], где [math]N[/math] - это уже упомянутая длина вектора(она же ширина матрицы), а m - высота матрицы.

Высота ЯПФ операции умножения вектора на число равна [math]\frac{N}{p}[/math], а ширина [math]p[/math].

Высота ЯПФ операции вычисления разности векторов равна [math] \log_2 p [/math], а ширина [math]p[/math].

В конечном счете общую высоту ЯПФ одной итерации алгоритма можно оценить, как [math]6 \sqrt N-3 + 4N + 3 + 1 + 3\lceil \frac{N}{p} \rceil + 2 \lceil \frac{N}{p} \rceil = 4N + 6 \sqrt N + 5 \lceil \frac{N}{p} \rceil + 1[/math], а ширину, как [math]2 \sqrt N[/math], если не брать в рассчет проверку критерия сходимости и упрощенности первой итерации по сравнению с остальными.

1.9 Входные и выходные данные алгоритма

Входные данные

1. Матрица [math]A \in R^{N \times N}[/math] ( [math]C^{N \times N}[/math] )
2. Вектор правой части [math]b \in R^N[/math] ( [math]C^N[/math] )

Выходные данные:

1. Вектор решения СЛАУ [math]x \in R^N[/math] ( [math]C^N[/math] )

1.10 Свойства алгоритма

BiCGStab хорошо зарекомендовал себя для решения систем линейных алгебраический уравнений, поскольку обладает некоторыми важными свойствами:

1. Благодаря применению подхода Петрова-Галеркина и техники ортогонализации, он численно устойчив
2. Не меняется вид матрицы в процессе решения
3. Эффективен для решения систем большой размерности с разреженной матрицей, поскольку в методе самая трудоемкая операция - умножение матрицы на вектор
4. Лучше подходит под распределенные системы, поскольку не содержит операции транспонирования матрицы
5. Применим для решения систем с несимметричными матрицами
6. Вычислительная мощность: [math]N/4[/math]

2 Программная реализация алгоритма

2.4 Масштабируемость алгоритма и его реализации

2.4.2 Масштабируемость реализации алгоритма

Исследование масштабируемости реализации стабилизированного метода бисопряженных градиентов проводилось согласно методике на суперкомпьютере "Ломоносов" Суперкомпьютерного комплекса Московского университета.

Набор и границы значений изменяемых параметров запуска реализации алгоритма:

• число процессоров [2 : 16] с шагом 1;
• размер матрицы [262144 : 11239424].

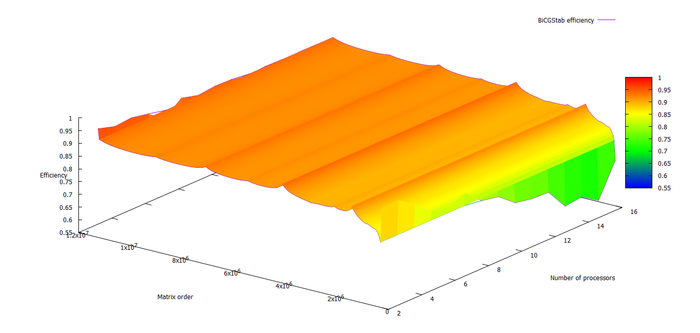
В результате проведённых экспериментов был получен следующий диапазон эффективности реализации алгоритма:

• минимальная эффективность реализации 60,00%;
• максимальная эффективность реализации 98,33%.

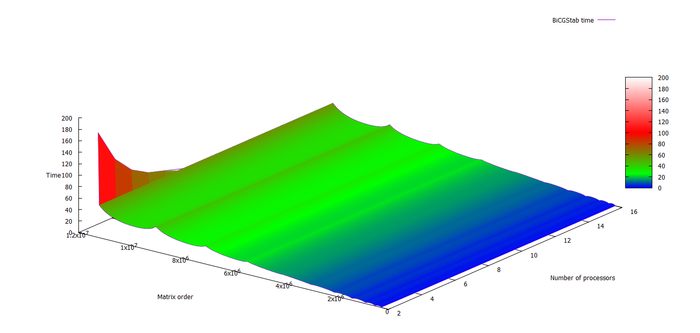
На следующих рисунках приведены графики производительности и эффективности выбранной реализации стабилизированного метода бисопряженных градиентов в зависимости от изменяемых параметров запуска.

Параллельная реализация стабилизированного метода бисопряженных градиентов. Изменение производительности в зависимости от числа процессоров и размера матрицы.

Параллельная реализация стабилизированного метода бисопряженных градиентов. Изменение эффективности в зависимости от числа процессоров и размера матрицы.

Исследованная параллельная реализация на языке C

2.7 Существующие реализации алгоритма

• Параллельная реализация алгоритма, предложенная MIT: MIT BiCGStab
• Параллельная реализация алгоритма в бесплатной библиотеке, поддерживающей MPI и OpenMP, HYPRE: Официальная страница Исходный код
• Параллельная реализация алгоритма на CUDA в условно бесплатной библиотеке NVIDIA AmgX

3 Литература

<references \>